Математика жизни и смерти. Часть 2. 7 математических принципов, формирующих нашу жизнь. Кит Йейтс.
Следующая тема: Математические законы: расследование роли математики в юриспруденции.
разберем Дело Дрейфуса — дело французского офицера, сосланного на каторгу за преступление, которого он не совершал.
В 1894 году французская уборщица – она же сотрудник контрразведки, работавшая под прикрытием в немецком посольстве в Париже, – нашла выброшенную записку.
Ее автор предлагал немцам купить французские военные секреты.
Находка спровоцировала лихорадочный поиск «крота» среди высшего офицерства французской армии.
Французская «охота на ведьм» окончилась арестом офицера, еврея, капитана Альфреда Дрейфуса.
французские власти обратились к главе парижского «Бюро по установлению личности» Альфонсу Бертильону, который никогда не был специалистом по почерковедению.
Бертильон в довольно невнятном заключении путано утверждал, что Дрейфус намеренно исказил свой почерк, дабы создать ложное впечатление, что кто-то попытался подделать записку.
В доказательство Бертильон представил замысловатый математический анализ, основанный на ряде сходств отдельных штрихов пера в повторяющихся многосложных словах в записке.
Он утверждал, что вероятность сходства между штрихами в начале или в конце любой пары повторяющихся слов составляет 1/5.
Далее он подсчитал, что вероятность четырех совпадений, обнаруженных им среди двадцати шести начал и окончаний тринадцати повторяющихся многосложных слов, составляла 1/5 в кубе, что давало ничтожное соотношение 16 к 10 000, и сделал вывод, что случайное появление таких сходств было крайне маловероятным.
Бертильон предположил, что это сходство «вероятнее всего, стало результатом тщательных и целенаправленных действий, что выдает преднамеренность – возможно, шифр.
Лишь Анри Пуанкаре, один из самых выдающихся математиков 19 века, удалось разобраться в хитросплетениях бертильоновских формул.
Через десять лет после того, как Дрейфусу был вынесен приговор, Пуанкаре привлекли к делу, и он быстро обнаружил ошибку в расчетах Бертильона.
Вместо того чтобы вычислить вероятность четырех совпадений в списке из 26 начал и окончаний в тринадцати повторяющихся словах, Бертильон вычислил вероятность четырех совпадений в четырех словах, что, естественно, гораздо менее вероятно.
Реальная вероятность тех четырех совпадений, которые выделил Бертильон, составляет примерно 18 к 100, что в 100 с лишним раз больше числа, которое он предъявил суду.
Пуанкаре смог опровергнуть некорректные результаты почерковедческого анализа и тем самым оправдать Дрейфуса.
честь Дрейфуса была восстановлена, и он продолжил службу своей стране на полях Первой мировой войны, отличившись на передовой в Вердене.
Дело Дрейфуса демонстрирует как силу математически подкрепленных аргументов, так и легкость, с которой ими можно злоупотреблять.
Математическая формула создает иллюзию достоверности.
От презумпции виновности отказались почти все страны, поскольку эта практика неизбежно производит больше ложноположительных и меньше ложноотрицательных результатов.
Однако и сегодня в некоторых странах юридические практики склоняются скорее к презумпции виновности, чем невиновности.
В японской системе уголовного правосудия, например, доля обвинительных приговоров составляет 99,9 %, причем большинство из них подтверждаются признанием вины.
Для сравнения: в 2017–2018 годах в уголовном суде Великобритании доля обвинительных приговоров составляла 80 %.
Высокая доля обвинительных приговоров в Японии впечатляет – как и эффективность полиции, ведь арестованный оказывается виновным в 999 с лишним случаях из 1000.
Но насколько это вероятно?
Такой высокий процент обвинительных приговоров частично объясняется жесткими методами допроса, которые практикуют японские следователи.
Ситуацию усугубляет давление, которое начальство оказывает на следователей, требуя от них сначала получить признательные показания, а улики и прочие доказательства расследования – уже потом.
(Ошибка независимости).
Два события считаются зависимыми, если знание о том, что произошло одно из них, влияет на вероятность происхождения другого.
(Табл. 3-4.).
Рассмотрим еще одну ужасную судебную ошибку.
У Салли Кларк от синдрома внезапной детской смерти (СВДС) с разницей в несколько лет умерло двое маленьких сыновей.
Английское правосудие обвинило ее в убийстве своих детей.
Рассмотрим, какие ошибки совершило обвинение.
Первой ошибкой следователя Мидоу было предположение, что случаи синдрома внезапной детской смерти (СВДС) являются полностью независимыми событиями.
Известно много факторов повышения риска СВДС.
обнаружили множество и генетических факторов, также увеличивающих вероятность СВДС.
У родных братьев и сестер много общих генов – соответственно, риск развития СВДС у них выше.
в Великобритании ежегодно происходит хотя бы один случай СВДС у второго ребенка.
смоделируем ситуацию, в которой мы сможем вычислить аналог вероятности смерти от СВДС.
Возьмем десять мешочков с мраморными шариками.
В девяти таких мешочках по десять белых шариков.
В десятом же – девять белых и один черный.
(Рис. 9. Древо решений для поиска вероятности выбора черных или белых шариков).
Для вычисления вероятности выбора черного или белого шарика при каждой попытке следуйте за соответствующими ветвями древа и умножайте вероятности на каждом шаге.
Так, вероятность вытащить черный шарик с первой попытки составляет 1/100.
При второй попытке мы выбираем из того же мешка, который мы выбрали при первой попытке.
Если на первом шаге вы вытянули черный шарик, то вы знаете, что и во второй раз выбираете из набора, в котором этот шарик точно есть.
Это значительно повышает вероятность выбора черного шарика – до 1 из 10, а не 1 из 100.
древо решений для поиска вероятности выбора черных или белых шариков можно подробнее изучить в табличке под видео.
В случае с вероятностью смерти второго ребенка от СВДС, если первый умер от этого синдрома, математика аналогична – вероятность растет.
Следователь проигнорировал тот факт, что оба ребенка Салли Кларк были мальчиками и что СВДС у мальчиков развивается почти в два раза чаще, чем у девочек.
Учет этого фактора подорвал бы позиции обвинения, показав более высокую вероятность серийной смерти от СВДС.
В этом свете шанс, что Салли убила двух своих детей, представляется соразмерно ниже.
(Экологическая ошибка).
Один из видов экологической ошибки – это поверхностное допущение, что обо всей разнообразной популяции можно судить по одному статистическому параметру.
Так, в Великобритании в 2010 году средняя ожидаемая продолжительность жизни женщин составляла 83 года, а мужчин – всего 79 лет.
Общая ожидаемая продолжительность жизни населения, таким образом, составила 81 год.
Но утверждение, что любая случайно выбранная женщина будет жить дольше, чем любой случайно выбранный мужчина, сделанное на основании того, что средняя ожидаемая продолжительность жизни у женщин выше, чем у мужчин, и будет типичным примером экологической ошибки.
Этот тип ошибки имеет собственное (очень подходящее) название – абстрактное обобщение.
Другая распространенная экологическая ошибка – утверждение, что «мы все живем дольше», основанное на поверхностной интерпретации данных об увеличении общей продолжительности жизни. Им часто злоупотребляют ленивые журналисты.
Говорить, что все будут жить дольше, чем ожидалось прежде, нельзя.
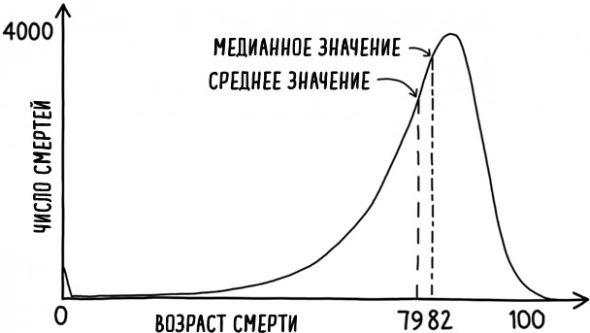
(Рис. 11. Возрастная зависимость числа смертей).
Возрастная зависимость числа смертей в год у мужчин в Великобритании следует искаженному распределению.
Средний возраст смерти составляет чуть менее 79 лет, в то время как медианный возраст – 82 года.
Распределение возраста смерти британских мужчин явно далеко от симметрии.
Поэтому подобные распределения обычно называют «смещенными» или «асимметричными».
Распределение доходов домохозяйств – это еще один статистический показатель, медианное значение которого сильно отличается от среднестатистического.
Большинство домохозяйств Великобритании имеют низкий располагаемый доход, но есть небольшое, но статистически значимое число богатых, которое искажает симметрию распределения.
Поначалу еще более удивительным примером кажется старая загадка:
«Каков шанс на то, что у следующего человека, которого вы встретите на улице, ног будет больше, чем в среднем у людей?»
Ответ: «Почти наверняка».
Соль в том, что одноногих или вовсе безногих калек очень немного, но они и обеспечивают некоторое снижение среднего количества ног в пересчете на все население.
Так что каждый, у кого две ноги, имеет больше ног, чем все население в среднем.
Этот пример показывает, насколько смехотворны попытки оценивать индивидуальные качества, исходя из усредненных показателей по всей популяции.
Очевидно, что использование некорректного усреднения для описания популяции может привести к экологическим ошибкам.
Еще один тип экологической ошибки, известный как парадокс Симпсона, возникает, когда мы пытаемся взять среднее значение из двух и более разнородных групп данных.
Парадокс Симпсона проявляется в самых разных областях – от оценки состояния экономики до интерпретации социально-демографических электоральных профилей и, что, возможно, наиболее важно, в разработке лекарств.
Экологическая ошибка следователя Мидоу, своевольно зачислившего Кларков в категорию семей, где риск развития СВДС низок, сделала смерть их двух детей в глазах присяжных гораздо более подозрительной, чем она выглядела бы, если бы присяжные исходили из других, более высоких показателей этого риска.
Огрехи такого рода встречаются в судопроизводстве настолько часто, что заслужили собственное имя – ошибка прокурора.
Доводы строятся на допущении, что если подозреваемый действительно невиновен, то появление определенных доказательств или свидетельств против него крайне маловероятно.
Из чего прокурор делает заключение – неоправданное – о том, что наличие таких свидетельств или обстоятельств делает вину подозреваемого весьма вероятной.
Для Салли Кларк таким допущением стало утверждение, что вероятность двух детских смертей подряд составляет всего 1 на 73 миллиона.
Но этот логический конструкт не принимает во внимание иные возможные альтернативные сценарии, в которых подозреваемая невиновна – например, смерть детей Салли по естественным причинам.
В рамках этой логики игнорируется и возможность того, что версия обвинения (двойное убийство младенца в случае Салли), может оказаться столь же – если не более – маловероятной, как и версия невиновности подозреваемого.
исходя из одного-единственного доказательства, наиболее вероятный вывод должен состоять в том, что подозреваемый невиновен.
Вполне вероятно, следователь Мидоу и сам не понимал, что совершает ошибку, заявляя, что
«…шансы на естественную смерть детей в этих обстоятельствах очень, очень невелики – 1 на 73 миллиона».
и присяжным осталось заключить, что Салли, скорее всего, убила двух своих детей.
Смерть двух детей от СВДС подряд крайне маловероятна.
Однако само по себе это не дает полезной информации о том, насколько вероятно, что Салли убила своих детей.
В 1999 году присяжные признали Салли виновной, осудив ее большинством в 10 голосов против 2.
Сообщалось, что один из присяжных признался другу, что на их решение наибольшее влияние оказала статистика следователя Мидоу.
Салли была приговорена к пожизненному заключению.
Главным основанием для апелляции была неточность статистических выкладок.
Эксперты-статистики объяснили судьям суть экологической ошибки при определении степени риска развития СВДС в семье Кларков,
ошибочность предположения Мидоу о том, что серийные случаи детской смертности являются независимыми явлениями,
и, соответственно, некорректность примененной им формулы подсчета вероятности такой смерти в случае Кларков,
а также суть ошибки следователя, к которой сторона обвинения подтолкнула присяжных.
Суд над Салли Кларк – вовсе не единственный процесс, в котором вероятность была неправильно использована и неверно понята.
Систематические обзоры в медицине, например, анализируют несколько клинических тестов, каждый из которых сам по себе не содержит исчерпывающей оценки эффективности того или иного вида лечения из-за немногочисленности тестируемых.
Во время второй апелляции, в 2003 году, адвокаты Салли представили новые доказательства, которые были обнаружены уже после вынесения ей обвинительного приговора.
Результаты вскрытия Гарри, второго сына Салли, ясно указывали на наличие бактерии Staphylococcus в спинномозговой жидкости.
По мнению экспертов, эта инфекция с большой долей вероятности привела к возникновению бактериального менингита, который и стал причиной смерти Гарри.
Новых микробиологических свидетельств было вполне достаточно для того, чтобы признать приговор Салли несостоятельным, но судьи апелляционного суда заявили, что очевидное злоупотребление статистическими данными в ходе первоначального судебного разбирательства уже должно было стать достаточным основанием для удовлетворения первой апелляции.
В 2003 году Салли вышла на свободу. Она вернулась к своему мужу Стиву и их третьему сыну, которому к тому времени было четыре года.
Ничто не могло компенсировать те годы, что она провела в тюрьме по ложному обвинению в убийстве самых близких ей людей.
попав не в те руки, математика может воспрепятствовать совершению честного суда, лишая ни в чем не повинных людей средств к существованию, а в экстремальных случаях – и жизни.












