07 ноября 2021, 16:28
Делаем опционный калькулятор по биномиальным моделям оценки в Google Spreadsheet (часть 2)
Этот пост будет посвящен реализации модели Кокса-Росса-Рубинштейна (Cox-Ross-Rubinstein, CRR для краткости), самой известной и довольно простой. Модель основана на предпосылке о том, что приращение вверх и вниз (в нашей таблице это ячейки B15 и B16) предполагаются симметричными. Это значит, что при умножении приращения вверх на приращение вниз получится 1. Иными словами, если актив за первый временной шаг двинулся вверх, а за второй — вниз, то по итогам второго временного шага актив будет на стартовой точке (где он был до первого шага).
Напомню, что сейчас у нас в ячейках находятся произвольные фиксированные значения, и теперь нам предстоит заменить их формулами. Скопируем наш лист из первой части на новый лист и назовём новый лист CRR (по имени модели).
Для реализации расчета нам потребуется ввести еще два предварительных расчетных параметра — время до экспирации в долях года и время одного шага в долях года. Время до экспирации в долях года = Время до экспирации / 365 (дней в году, если считаете правильным учитывать только рабочие дни — то сюда подставляем 252, но я везде использую календарные). Время одного шага в долях года = Время до экспирации в долях года / Количество шагов (в нашем случае 5, совпадает с количеством дней до экспирации, мы все моделируем в днях).
Добавим расчетные параметры в ячейки B19 и B20, поименуем диапазоны TimePercent и StepTimePercent соотвественно:
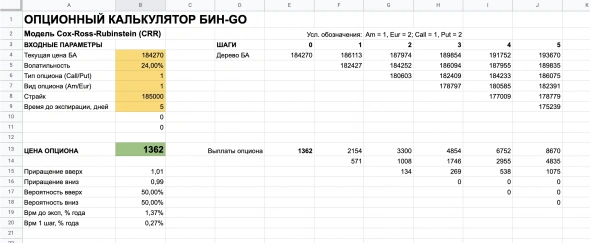
В модели CRR размеры приращений зависят от двух параметров: волатильность и длительность временного шага. Волатильность (sigma) — это один из входных параметров, а длительность шага мы с вами только что посчитали (StepTimePercent).
Приращение вверх, которое у нас находится в ячейке B15, будет рассчитываться по формуле:
Из предпосылки о симметричости приращений следует, что приращение вниз = 1 / приращение вверх. Вводим формулу в ячейку B16
Теперь наше Дерево БА в правой верхней части таблицы пересчиталось (ведь все формулы мы с Вами в предыдущей части ввели) в соответствии с моделью CRR. Отличительной чертой биномиальных деревьев, строящихся по модели CRR является симметричность относительно начальной цены (о чем выше уже было упомянуто). Вниз по дереву стартовая цена БА может встречаться среди цен узлов неоднократно.
Переходим к расчету вероятностей движения цены вверх или вниз. Так как у нас опцион на фьючерс, у нас нет ни interest rate, ни dividend yield, а значит формула упростится до такой:
И соответственно вероятность движения вниз будет равна 1 — вероятность движения вверх. Вводим формулы в ячейки B17 и B18.
Вуаля, дерево опциона тоже пересчиталось, показав нам в начальной ячейке E13 цену опциона Call по модели Кокса-Росса-Рубинштейна.
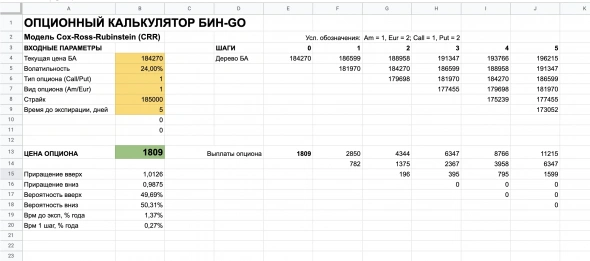
Опционный калькулятор по модели CRR готов. Если потребуется увеличить количество шагов — нужно будет достроить узлы деревьев. Количество рядов узлов должно совпадать с количеством периодов до экспирации (ячейка B9). Не очень удобно, зато обошлись без кодинга и макросов, ну и принцип поняли, надеюсь.
В следующей серии сделаем те же самые расчеты по другой биномиальной модели Джарроу-Рудда (Jarrow-Rudd).
А пока вот результат Чтобы редактировать документ и смотреть формулы, его надо сохранить себе — а доступ запрашивать не надо )
Напомню, что сейчас у нас в ячейках находятся произвольные фиксированные значения, и теперь нам предстоит заменить их формулами. Скопируем наш лист из первой части на новый лист и назовём новый лист CRR (по имени модели).
Для реализации расчета нам потребуется ввести еще два предварительных расчетных параметра — время до экспирации в долях года и время одного шага в долях года. Время до экспирации в долях года = Время до экспирации / 365 (дней в году, если считаете правильным учитывать только рабочие дни — то сюда подставляем 252, но я везде использую календарные). Время одного шага в долях года = Время до экспирации в долях года / Количество шагов (в нашем случае 5, совпадает с количеством дней до экспирации, мы все моделируем в днях).
Добавим расчетные параметры в ячейки B19 и B20, поименуем диапазоны TimePercent и StepTimePercent соотвественно:

В модели CRR размеры приращений зависят от двух параметров: волатильность и длительность временного шага. Волатильность (sigma) — это один из входных параметров, а длительность шага мы с вами только что посчитали (StepTimePercent).
Приращение вверх, которое у нас находится в ячейке B15, будет рассчитываться по формуле:
=EXP(sigma*SQRT(StepTimePercent))
Из предпосылки о симметричости приращений следует, что приращение вниз = 1 / приращение вверх. Вводим формулу в ячейку B16
=1/UpMoveПолучится, что за одни сутки базовый актив подрастает на 1,26% вверх или падает на 1,25% вниз. Приращения получились неравными.
Теперь наше Дерево БА в правой верхней части таблицы пересчиталось (ведь все формулы мы с Вами в предыдущей части ввели) в соответствии с моделью CRR. Отличительной чертой биномиальных деревьев, строящихся по модели CRR является симметричность относительно начальной цены (о чем выше уже было упомянуто). Вниз по дереву стартовая цена БА может встречаться среди цен узлов неоднократно.
Переходим к расчету вероятностей движения цены вверх или вниз. Так как у нас опцион на фьючерс, у нас нет ни interest rate, ни dividend yield, а значит формула упростится до такой:
=((1-DownMove)/(UpMove-DownMove))
И соответственно вероятность движения вниз будет равна 1 — вероятность движения вверх. Вводим формулы в ячейки B17 и B18.
Вуаля, дерево опциона тоже пересчиталось, показав нам в начальной ячейке E13 цену опциона Call по модели Кокса-Росса-Рубинштейна.

Опционный калькулятор по модели CRR готов. Если потребуется увеличить количество шагов — нужно будет достроить узлы деревьев. Количество рядов узлов должно совпадать с количеством периодов до экспирации (ячейка B9). Не очень удобно, зато обошлись без кодинга и макросов, ну и принцип поняли, надеюсь.
В следующей серии сделаем те же самые расчеты по другой биномиальной модели Джарроу-Рудда (Jarrow-Rudd).
А пока вот результат Чтобы редактировать документ и смотреть формулы, его надо сохранить себе — а доступ запрашивать не надо )
Читайте на SMART-LAB:
🔔 День инвестора ДОМ.РФ – уже завтра!
Уже завтра, 18 февраля , подведём финансовые итоги 2025 года и поделимся планами на будущее.
Будем вести трансляцию в VK , Rutube и на нашем сайте .
❗️ Стартуем в 16:00 – не...
13:08

За первые полтора месяца года передали покупателям более 2700 ключей
Друзья, привет! Пока наши котировки волатильны на информационном шуме, операционно Группа продолжает достигать поставленные цели — за первые полтора месяца года передали покупателям более 2700...
11:54











Можете подсказать как получить кривую (улыбку) волатильностей при заданной IV центрального страйка в qlua-скрипт для контракта Si?