Облигации: мифы и реальность. Часть 3. Глава 2. Очертания будущего.

Грядущее под диктовку ФРС

В одном из недавних топиков на смартлабе мое внимание привлек сюжет из финансового шоу про страдающие от бессонницы деньги

Помимо привычных слов о скором обвале фондового рынка ведущий пообещал рассказать и о том, что такое облигации и кривая доходности. Захотелось узнать об этом подробнее.  Всё оказалось просто и понятно, эксперт разложил информацию по полочкам: 

Когда вы покупаете облигации, вы даете в долг — правительству или компании. Норма дохода по облигации, которую вы желаете получить, обусловлена  степенью вашего доверия к заемщику. Банкротной компании нельзя давать деньги под 3% годовых, но под 30% — почему бы и нет, — ведь мы понимаем, что она за год не дефолтнёт (Л — логика). На самом  деле всё зависит от кривой доходности,  потому что она диктует нам будущее. 

На простом жизненном примере ведущий объясняет почему требуемая доходность растет со сроком до погашения: 

Можно дать деньги знакомому Васе на три часа, и это будет почти безрисковая операция, а можно на год,  но за год может произойти все что угодно, например, Вася сдохнет.  Поэтому на длинном горизонте совершенно другие риски. Зачем я буду рисковать? Доживет — не доживет. Пусть деньги отбивают инфляцию, чтобы я не потерял.  

Как могут быть связаны возможный уход знакомого Васи из жизни и инфляция, я, признаться, не очень понял, но рассуждения про увеличивающиеся со временем до погашения облигации риски звучат совершенно логично. 

Далее ведущий нарисовал кривую доходности в виде части параболы: Это нормальная форма кривой.  Чем больше срок до погашения, тем выше премия за риск.  Но есть другие разновидности кривой доходности, нарушающие это правило: кривые могут не только расти, но и убывать со сроком до погашения, как если бы одалживающий у вас деньги Вася  подобно старому вину со временем только хорошел. И этому тут же нашлось объяснение: в последние годы исказилось всё из-за этих печатных станков. В Европе и Японии всё делается через одно место. Кривая доходности может плавать в зависимости от того, что происходит в экономике страны. Всегда подкупает, когда сложные и непонятные  ситуации получают простые и ясные решения. Здесь я полностью солидарен с Валентиной Терешковой: зачем крутить и мудрить, зачем городить какие-то искусственные конструкции?

Как выяснилось, эксперт  полностью изучил всё, чем занималась ФРС на протяжении последних ста лет. Он пришел к выводу, что эта организация лажает всегда. От последних заявлений членов ФРС у него идут мурашки по коже. Ведь они буквально всем вешают на уши лапшу и кормят завтраками. Еще ведущий рассказал о спреде 10-2 и инверсии кривой доходности. Наконец, стало понятно, почему весной 2021 нас ожидает крах рынков — автор обнаружил в рыночных данных очень тревожный сигнальный паттерн: один в один повторяется ситуация, предшествовавшая прошлым обвалам. После инверсии спреды развернулись и угрожающе растут. “С Люсей то же самое было перед тем как ее в больницу увезли”

Надо отметить, что сильные эмоции ведущего в отношении лживости и некомпетентности ФРС мне действительно близки. Меня так же как и его раздражает этот утомительный бесконечный рост. Ведь я в нем не участвую, потому что, как и многие другие созерцатели рынка, все время ожидаю обвала, который к всеобщей досаде постоянно откладывается.

Но вернемся к нашим баранам.  Ведущий, рассуждая о нормальной форме кривой доходности  транслирует основные положения теории предпочтения ликвидности (о чем, возможно, не догадывается, подобно  господину Журдену, не знавшему, что он разговаривает прозой)  и одновременно  ссылается на возможность дефолта умозрительного Васи. Однако вероятность дефолта контрагента может быть важна для маленького банка или страховой компании, а когда мы смотрим на рынок гособлигаций  в контексте срока до погашения, всерьез рассуждать о ней, конечно же, нельзя. Примеры с внезапно отбросившим коньки Васей в данном случае неуместны. С другой стороны, в корпоративных облигациях наши вероятности дефолтов уже учтены в спредах к кривой доходности. 

Как любой нормальный человек, никогда не работавший в банке и не изучавший теорию вероятности, ведущий шоу путает две вещи: 

1) кумулятивную вероятность дефолта (на протяжении какого-то срока), которая нужна для ответа на вопрос: вероятность какого события больше — банкротство случится на протяжении следующих 10 лет или на протяжении следующих 20 лет? Понятно, что так как второе событие включает в себя первое, то в силу  неотрицательности и аддитивности вероятностной меры оно имеет более высокую вероятность (точнее не меньшую)

2) интенсивность дефолта, или вероятность того, что дефолт наступит в течение короткого отрезка времени, при условии, что он не произошел в предыдущий период. Эта величина на момент оценки считается постоянной, она инкорпорируется в процентную ставку. При рассмотрении редуцированных моделей зачастую предполагается, что события дефолтов подчиняются пуассоновскому процессу.

Банк постоянно мониторит состояние заемщика, обкладывает его ковенантами и выдает кредиты под надежные залоги, так что ему нечего особо беспокоиться о том, что будет через 10 лет — любые проблемы он замечает сразу и, в случае чего, может требовать досрочного погашения. Зачем ему пытаться оценить вероятность банкротства компании в 8-м или 10-м году, он ориентируется на текущую ситуацию и краткосрочный прогноз. Проценты банк получает ежемесячно. А еще лучше, если это аннуитетные платежи. На рис. 1 видно, каким образом с течением времени аккумулируется ожидаемая прибыль от разницы в процентных ставках между безрисковым займом и относительно надежным корпоративным заемщиком:

 

Разница в прогнозном валовом доходе растет нелинейно (действует магия сложного процента), компенсируя кумулятивную вероятность дефолта. Для держателей корпоративных и суверенных бондов на рынке деривативов  присутствует  своя мера оценки риска дефолта  (и, одновременно, инструмент защиты) — кредитные дефолтные свопы. 

 Однако для торгующихся на рынке облигаций действительно важен процентный риск, который тем выше, чем больше срок до погашения. Для дальнего конца кривой он может быть в том числе связан с ожидаемой инфляцией. Но откуда известна будущая инфляция? Точнее, почему имеется уверенность, что инфляция будет только расти, а ведь именно это должно подразумеваться возрастающей кривой доходности при данной предпосылке. Если инфляция постоянна, то такая форма кривой вовсе не обязательна. Почему кривые доходности могут быть иногда плоскими, изогнутыми или даже убывающими функциями срока до погашения? Одних глупых действий ФРС, Европы и Японии, действующими “через одно место” для этого явно не достаточно. Можно задать еще много “почему”, смазывающих четкую картину мира ведущего, однако следует признать, что на самом деле теорий временной структуры процентных ставок несколько, и  объяснить все наблюдаемые формы кривой какой-то одной из них не получится.

  Немного отвлечемся и сделаем несколько общих замечаний, чтобы освежить в памяти материал прошлых частей. Ставки  в американских изданиях чаще всего указываются в виде так называемого bond equivalent yield (BEY) Это номинальные ставки при полугодовом начислении процентов (формула 2 из части 1). Номинальные ставки удобны тем, что когда они применяются к конкретному периоду, их просто делят на число периодов начисления процентов (нет компаундинга) Если, например, задана спотовая кривая вида r_0.5= 4%, r₁=4.5%, цена полугодовой облигации находится как 1000/(1+4%/2)=980.39, а годовой как 1000/(1+4.5%/2)² =956.47

В российской традиции на кривой бескупонной доходности указана эффективная доходность с годовым начислением процентов (формула 4 из части 1).  Если использовать те же значения из примера  r_0.5= 4%, r₁=4.5%, цена облигации с погашением через полгода будет равна 1000/(1+4%)^0.5  = 980.58, а цена годовой: 1000/(1+4.5%) =956.94. 

 

На самом деле, как мы хорошо помним, первичны всегда цены облигаций, а уж какую доходность мы из них извлечем — номинальную, эффективную, текущую, с каким видом начисления процентов и т.д. — это уже наше дело. Именно потому, когда говорят, что инвесторы требуют такую-то доходность, не конкретизируя, что именно имеют ввиду, это зачастую приводит к недопониманию и ошибкам в расчетах. Доходности важны и удобны для теоретических изысканий, они просты в применении, и у них нет сроков погашения, но все безарбитражные доводы строятся только на ценах облигаций и их денежных потоках. Практики зачастую работают не с доходностями напрямую, а с дисконт-факторами (текущая стоимость 1 ден. единицы, получаемой в будущем)  и строят дисконтные кривые вместо кривых доходностей. В наших примерах мы зачастую будем использовать непрерывное  начисление процентов как одно из самых удобных. Мы можем легко переходить от непрерывного начисления процентов к ежегодному с помощью преобразования  exp(y∙T)=(1+ r)^T

Понятие о форвардных ставках.

В дальнейшем нам понадобится представление о подразумеваемых форвардных ставках. Они естественным образом возникают в следующей гипотетической ситуации. Предположим, клиент приходит в банк и говорит: “Я хочу взять кредит на год, но не сейчас, а через год. Какую ставку вы мне можете гарантировать  на этот момент, если мы сейчас подпишем обязывающие документы?” Возможно, клиент опасается неблагоприятного развития ситуации на рынке заимствований — взрывного роста инфляции и  краткосрочного повышения ставок. С целью упростить пример допустим, что банк  приравнивает кредитный рейтинг клиента к рейтингу государственных обязательств страны. Пусть банк наблюдает текущую кривую доходности: {r₁=4%, r₂ =5% => P(0,1) =100/(1+r₁)= 96.15, P(0,2) =100/(1+r₂)² = 90.70} Тогда он может легко зафиксировать годовую форвардную ставку ₁f₁ (т.е., ставку, действующую с первого года на второй)  путем следующих операций. Банк  продаст в короткую одну двухлетнюю бескупонную облигацию за 90.70 и на вырученные деньги купит P(0,2)/P(0,1) = 0.943  частей однолетней (опять же ради простоты допустим, что облигации можно приобретать “дробными” частями). Начальные затраты у банка будут нулевые, т.к. 0.943·96.15=90.70. Через год короткая облигация будет погашена, что принесет банку 90.70·(1+r₁) = 94.33  наличных и эти деньги он может выдать клиенту на год в кредит. 

Поскольку еще через год сам банк должен будет вернуть номинал (100) от проданной ранее двухлетней облигации, то изначально он должен назначить клиенту такую  годовую форвардную ставку ₁f₁ , чтобы выполнялось условие отсутствия арбитража: 100= 94.33·(1+₁f₁ ), откуда легко вычислить ₁f₁  = 6%

 

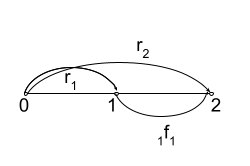
Если вернуться к ценам облигаций, можно записать выражение для ₁f₁: 

1 + ₁f₁ = P(0,1)/P(0,2). Это же условие можно записать, используя только  ставки: (1+r₂)² = (1+₁f₁)(1+r₁) Отсюда наглядно видно, что ₁f₁ является “ставкой безубыточности”,  обеспечивающей равенство стратегий: 1) купить двухлетнюю облигацию, или 2) купить короткую облигацию, а через год реинвестировать еще на год.

Похожие рассуждения можно провести для любого периода в будущем и вывести простое соотношение для спотовых и форвардных ставок (в данном случае запись _mf_n означает, что ставка применяется для года m и действует n лет)

                           (1+r_n+m)^n+m = (1+_mf_n)ⁿ(1+r_m)^m

В самом общем случае форвардная ставка – это такая устанавливаемая сегодня процентная ставка,  которая будет выплачена за пользование деньгами, занятыми на некоторый определенный срок в определенный момент в будущем.

 Существует несколько форм записи для форвардной ставки. Иногда пишут f_mn или f(m,n) и подразумевают, что ставка действует с года m по год n (а не n лет). Для годовых форвардных ставок могут использовать обозначение f_m  — это краткосрочная форвардная ставка, действующая с года m до года m+1. При непрерывном начислении процентов используют так называемую мгновенную форвардную ставку f(0, t). Она получается из обычной  форвардной ставки F(0,t,T) -  (ставки назначаемой в момент времени 0, начинающей действовать в момент t, до момента T) путем предельного перехода t→T. Мгновенная форвардная ставка начисляется на бесконечно малый отрезок времени в будущем.

Однолетние форвардные ставки образуют так называемую кривую краткосрочных форвардных ставок. Она приведена на рис 2 для примера из прошлой части.

 

Можно показать, что эти форвардные ставки f_i ( i < n, f₀ = r₁ ) связаны со спотовой ставкой r_n соотношением, 

                        (1+f₀)(1+f₁)(1+f₂)..(1+f_n-1) = (1+r_n)ⁿ

т.е. спотовая ставка — это среднее геометрическое соответствующих ей годовых форвардных ставок. Поэтому, при положительном наклоне спотовой кривой наша форвардная кривая всегда лежит выше, а ее форма определяется крутизной наклона спотовой кривой. При выходе кривой бескупонной доходности на плато такая форвардная кривая к ней фактически примыкает. Поскольку между спотовыми и форвардными ставками устанавливается взаимно однозначное соответствие, последние наравне со спотовыми могут использоваться для дисконтирования денежных потоков по облигации. Помимо этого форвардные ставки нужны для оценки контрактов FRA и процентных свопов.

Поскольку спотовая кривая порождает целое семейство форвардных кривых (не только для краткосрочных ставок), с их помощью можно построить “ожидаемую” (т.е. подразумеваемую текущей временной структурой) динамику спотовых кривых во времени. Например, подразумеваемая спотовая кривая через год — это форвардные ставки с 1-го года на второй, с 1-го на третий, и т.д. Мы как бы движемся вперед во времени и наблюдаем всё уменьшающийся кусочек видоизменяющейся спотовой кривой “из будущего”. 10 летний форвард на рис. 3  — ожидаемый через 10 лет вид спотовой кривой  для следующих 11 лет.  А 15-летнему форварду соответствует подразумеваемая через 15 лет спотовая кривая, состоящая всего из 6 точек. Таким образом, предполагается, что инвестор через 15 лет будет наблюдать убывающую кривую бескупонной доходности (по крайней мере на протяжении первых шести лет)

 

Поэтому зачастую пишут, что форвардные ставки отражают мнение рынка о будущих процентных ставках  (более подробно это будет рассмотрено при обсуждении теории ожиданий) Однако для непрофессионального участника рынка практическая польза от них следующая: они помогают принять решение, например, в выборе между стратегиями 1) покупка и удержание двухлетней облигации и 2) последовательная “перекладка” из одной короткой облигации в другую. Если инвестор уверен, что в следующем году краткосрочные ставки вырастут сильнее, чем подразумеваемая форвардная ставка, для него имеет смысл находиться в коротких облигациях (при горизонте инвестирования два года) 

 В следующей части этой же главы мы непосредственно перейдём к обсуждению гипотез, объясняющих временную структуру и поймём, почему кривые доходности не выглядят так, как их нам рисует Василий Олейник.