04 ноября 2019, 20:28
Контроль рисков в играх с рекапитализацией
Сложность задачи контроля рисков состоит в том, что риски в действительности не ограничены и нарастают с течением времени так, что превращают бесконечно длительные игры с полной рекапитализацией в игры с абсолютно неконтролируемым риском. В связи с чем, задача выбора оптимального плеча (объёма) становится в общем случае математически не решаемой, а риск-менеджмент, в конечном счете, определяется только психологическим комфортом управляющего или инвестора. Тем не менее, исходя из некоторых предпосылок мы можем ограничить зону допустимого психологического комфорта и склонности к риску, то есть указать на некоторые их разумные пределы.
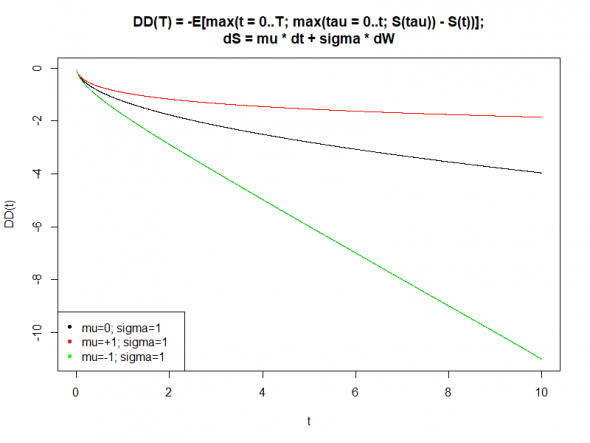
Изображение зависимости средней ожидаемой максимальной просадки заданных стратегий от времени. Любезно позаимствовано у Eugene Logunov.
Как и ранее, имея стартовый капитал 50 млн. долларов США мы будем пытаться обыграть господина Баффета, имеющего 500 млрд. долларов США, то есть будем стараться увеличить свой капитал в 10 000 раз за счёт игры на бирже. Играть мы будем нелинейно, то есть будем увеличивать ставки после каждого удвоения пропорционально текущему капиталу и поэтому для реализации нашей цели нам предстоит выиграть у господина Баффета не 10 000 раз подряд, а всего лишь:
Мы знаем, что наша стратегия обладает преимуществом над стратегией господина Баффета и позволяет играть против него с вероятностью 55%/45%, то есть с 10% смещением (Шарп = 1.6)
Нам так же известно, что уменьшая «плечо» и сокращая доходность, общая вероятность победы в серии испытаний (вероятность удвоения капитала) растёт пропорционально:
где n — необходимое число последовательных выигрышей для удвоения капитала, а 1/n — риск (волатильность) на сделку.
В этом случае вероятность закончить полную игру с положительным результатом, то есть, непосредственно разбогатеть, а не потерять, пропорциональна:
Рассмотрим поведение этих величин графически:
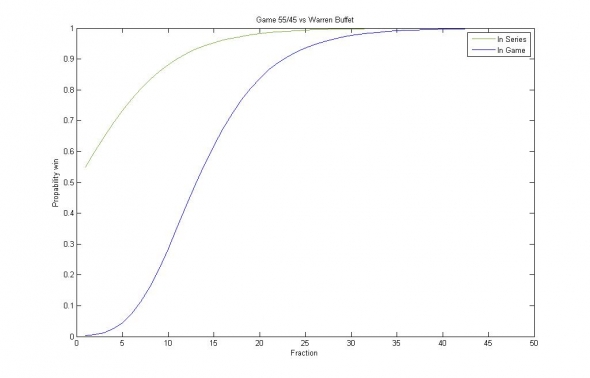
Изображение — вероятность увеличения капитала на 1млн.% (синяя линия), и вероятность удвоения капитала (зелёная линия) при дроблении капитала на n частей, отложенных по оси абсцисс для стратегии, обладающей годовым Шарпом 1.6.
Видно, что для стратегии данного качества (Шарп = 1.6), ограничение годовой доходности должно составлять около 60% годовых (риск = 1/40= 2.5%), а ограничение 3 сигма просадки на уровне 50%. В этом случае мы можем быть почти уверенными (>99.5%) в том, что стратегия не разорит нас на дистанции 1 млн. процентов. При ограничении 3-сигма просадки в 80%, доходности 75%, а ставки — 1/30 - мы будем увеличивать свой капитал на 1 млн.% только в 92% случаев.
Аналогично и для стратегий более низкого качества - требования к рекапитализации удовлетворяются при схожих ограничениях квантильных просадок на уровнях 20-25% (2 сигма) и 45-50% (3 сигма). Для показателя Шарпа 1, например, это соответствует риску 1/75 = 1.3% на сделку и ограничению доходности на уровне 20% годовых.
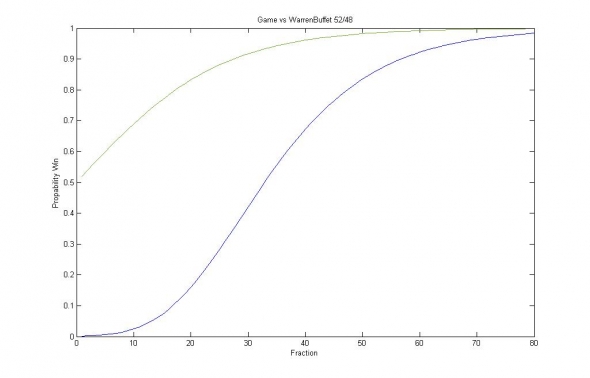
Изображение — вероятность увеличения капитала на 1млн.% (синяя линия), и вероятность удвоения капитала (зелёная линия) при дроблении капитала на n частей для стратегии, обладающей годовым Шарпом 0.6.
* Ограничение данной модели — полное отсутствие зачатков интеллекта у господина Баффета и стационарность среднего независимых испытаний, а не среднего независимых серий испытаний.
Читайте на SMART-LAB:

Как инвестирует Ярослав Кабаков
Поговорили с директором по стратегии ФГ «Финам» Ярославом Кабаковым — обсудили вредные инвестпривычки, выбор стратегии, использование ИИ и профессиональную интуицию. Делимся самыми...
20.02.2026
Технологии как новый драйвер: ключевые идеи инвестиционного форума ВТБ «РОССИЯ ЗОВЕТ!»
🧮 Главный тренд 2026 года — стабилизация и технологический поворот
Руководитель департамента по работе с клиентами рыночных отраслей ВТБ Дмитрий Средин:
Снижение ключевой ставки...
20.02.2026

Дебютный выпуск ПКО Вернем (B|ru|, 150 млн р.,YTM 29,97%) на 26 февраля
Информация для квалифицированных инвесторов 📌 26 февраля — новый облигационный дебют от коллекторского агентства «Вернем» ( B|ru| ) Предварительные параметры дебютного выпуска ПКО...
20.02.2026

Россети Ленэнерго. Отчет об исполнении инвестпрограммы за Q4 2025г. Опасения оправдались - обесценение съело прибыль
Компания Россети Ленэнерго опубликовала отчет об исполнении инвестпрограммы за Q4 2025г., где показаны финансовые показатели компании по РСБУ в 4 квартале (ну и понятно за целый год):...
20.02.2026










Eugene Logunov, если вы имеете ввиду вот это . То это наивернейший путь к сливу.
Взяв, например, игру 60/40, +1/-1, ставка составит 20%.
Синяя — счёт, зелёная — текущая просадка в долях от капитала (правая ось)