Метод Райана Джонса

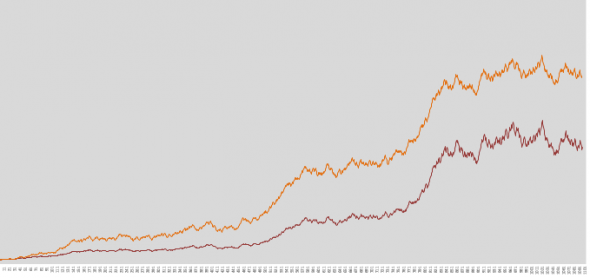
Разница доходов при фиксированном риске (2,5% — темная) и при наращивании позиции с помощью дельты. Искал такое соотношение, чтобы гладкость-кривизна линий у двух систем была почти одинаковой. Можно увеличить прибыль, рискуя 3%, но гладкость будет уже отличной от торговли дельтой. При равенстве — преимущество явное у дельтирования перед слепым %.
Торговля через дельту наращивания объемов — это т.н. фиксировано-пропорциональный метод Райана Джонса.
Это реально суперграаль (для супер последовательных плюсистов на бирже) или я в чем-то ошибаюсь?..

Райан Джонс

Remarka

Москва

133

2 720

с 30 апреля 2014

14 Комментариев

Московский Лоссбой
01 ноября 2019, 10:39
Ой, не читал. Стыдно мне.

Можно ссылочку?
0
Freeman Busido
01 ноября 2019, 10:39
А в чем грааль? Это давно известно и без этого автора. Чистая математика, до которой дойти может каждый, если конечно понимает. Книги почитай, которые были до Райана Джонса :))). И кто он вообще такой? Нашел на какой-то кухне пост и рад. А самому подумать? Зачем искать параметры? Составь уравнение — получишь ответ быстро, чем будешь искать и подбирать «гладкость» кривой. «Гладкость» кривой характеризуется расхождением, что в свою очередь описывается математически.
+1
XaMeJIeoH
01 ноября 2019, 13:41
Привет!

На мой личный взгдял подобные подходы хороши лишь для ретроспективы и «бумажной аналитики», живые методы олжны быть построены на адаптации.

Мои принципы следующие:
1. Скорость снижения сайза должна быть выше скорости его наращивания.
2. Должен быть определен размер репрезентативной серии (кол-во сделок на которой ты констатируешь «да, я иду в рамках системы»)
3. Общий риск при ручной торговле должен быть разделён — риск слома системы и риск исполнения. Соответственно, различные алгоритмы снижения сайза.

На твоёмграфике очевидны два периода исполнения системы — ранний, когда величина и скорость (глубина/кол-во сделок) просадок были поменьше и поздний, когдп существенно увеличились. Репрезентативный ряд раннего явно короче позднего (примерно 100 vs200). В чем присина изменения эквити? В рынке или исполнении? Если в первом, то надо в принципе пересматривать величину минимаольного репрезентативного ряда системы, а если во втором — что-то делать с оперативным контролем и управлением сайза (по типу как ты делал с МА 5,20).

В итоге, у тебя будет двузвенное управление сайзом.
Для последовательно плюсующей системы лучшим управлением сайза по системе будет пересмотр сайза после преодоления очередной репрезентативной серии (РС) { сайз=округлвниз($капитал/($ГО+$макс.сист.рискРС)) }, т.е. максимальная скорость наращивания.
А для последовательно плюсующего исполнения у тебя будет динамическое управление исполнительной частью риска на РС ($макс.исполн.рискРС).
В итоге формула примет общий вид:
сайз=округлвниз($капитал/($ГО+($макс.сист.рискРС+$макс.исполн.рискРС)))
+1
meat
01 ноября 2019, 14:37
ничего не понял, но было интересно
0

Читайте на SMART-LAB:

Евро игнорирует хороший ВВП: рынок прайсит риск ускорения роста ИПЦ

Евро четвертую сессию подряд отступает против доллара и во время лондонской сессии держится чуть выше 1.1850, постепенно сдавая важный психологический плацдарм на 1.19. Предварительные...

Tickmill

13.02.2026

Сделки в портфеле ВДО

Если Индекс ОФЗ (RGBI) пробьет вверх 117,51 п., то в портфеле PRObonds ВДО сокращаем короткую позицию во фьючерсе на него с ~2,3% до 2,1% от активов. Телеграм: @AndreyHohrin Не...

Иволга Капитал

13.02.2026

Рекомендации для эмитентов и переход к гибридным ЦФА — опыт Селигдара

Приняли участие в Alfa Talk «ЦФА: новая архитектура рынка», который был посвящен трансформации регулирования цифровых финансовых активов (ЦФА) и криптовалют. Обсудили и поделились...

ПАО СЕЛИГДАР

13.02.2026

Аренадата чудом выполнила гайденс. Сравнение с сектором по мультипликаторам. Прогноз результатов и дивидендов за 2025 год.

Вчера Аренадата опубликовала пресс-релиз . За 2 дня после выхода новостей акции росли максимально до +28%. Фокус пресс-релиза не на результате, а на том, что компания выполнила гайденс. Сам...