Фрактальная размерность
В давние времена, на сайте трейдеров Комон вели речь о заумных вещах, таких как:: Hurst exponent, Fractal dimension и тп. Недавно прочитал статью о фрактальных характеристиках временных рядов. Цитата: «Так, при 1,5 > D >1 временные ряды (валютных курсов, курсов акций и др.) имеют долговременную корреляцию, возникает персистентное состояние рынка, полностью характеризующееся показателем фрактальной размерности. Причем, близкое к единице значение фрактальной размерности указывает на скорое окончание действующего тренда. При D =1,5 с разбросом ± 0,05 поведение системы стохастическое и хорошо описывается классическими статистическими методами. При 2 > D >1,5, чем ближе D к двойке, тем более нелинейным становится временной ряд, возникает антиперсистентное состояние курса акций, временная кривая курса становится неустойчивой и готова перейти в новое состояние.» Решил попробовать применить к фьючерсу на Сбербанк ТФ =1 мин. 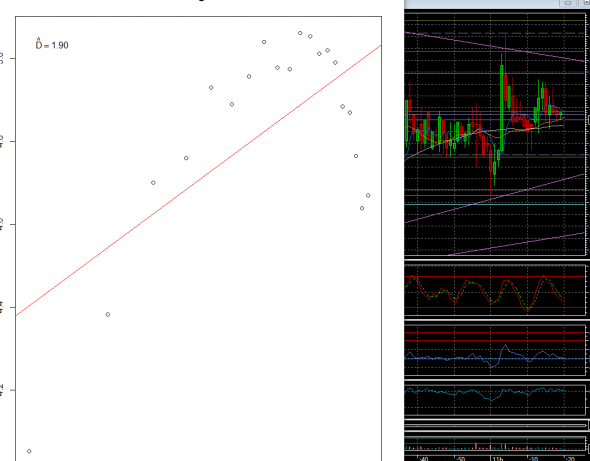
Первая картинка больше соответствует флэту, фрактальная размерность D=1.90
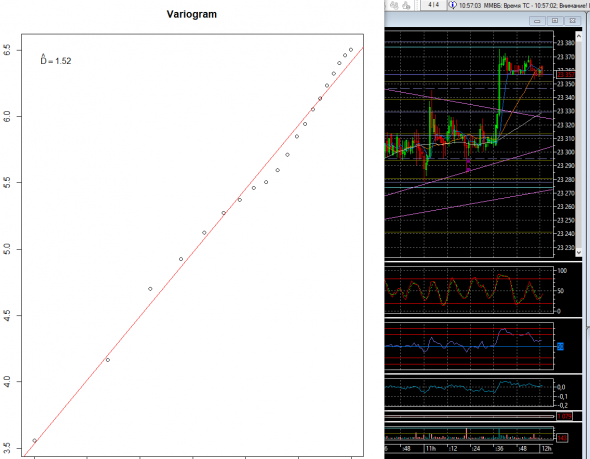
Вторая, D=1.52 изменения произошли после выхода из флэта вверх.
В динамике это выглядит достаточно интересно, но особой предсказательной силы фрактальная размерность не имеет, а как дополнение к другим методам будет интересно попробовать.
Например:
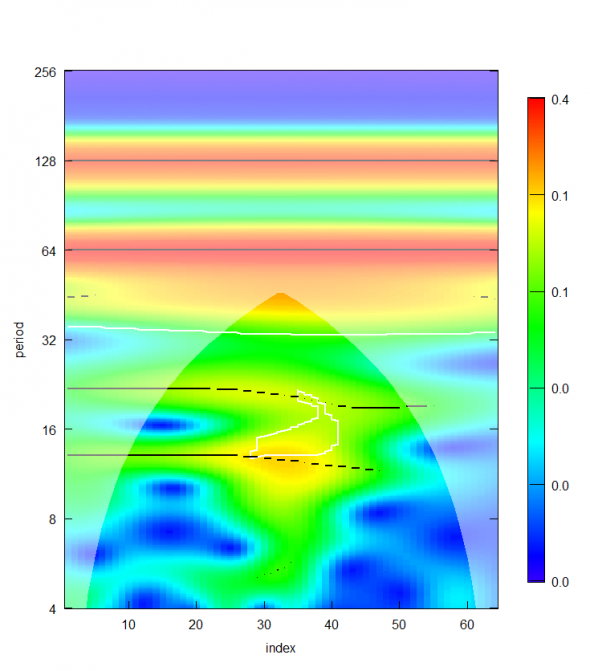
вместе с этой штуковиной, имеющей вычурное название: wavelet power spectrum.
 bozon14 октября 2019, 14:12Предсказательная сила в том, что всё так или иначе возвращается в h = 1/2 и в спектре временного ряда нет устойчивых линий Фраунгофера.0
bozon14 октября 2019, 14:12Предсказательная сила в том, что всё так или иначе возвращается в h = 1/2 и в спектре временного ряда нет устойчивых линий Фраунгофера.0













