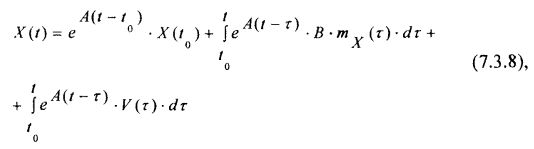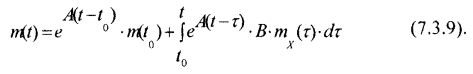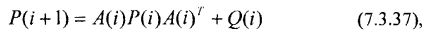Статистическая природа функционирования финансового рынка

Лауреатами Нобелевской премии по экономике 2013 года стали американские ученые-финансисты, занимающиеся ценообразованием на фондовых рынках: Юджин Фама, (Eugene F. Fama), Ларс Петер Хансен (Lars Peter Hansen) и Роберт Шиллер (Robert J. Shiller). Все трое, в особенности Юджин Фама и Роберт Шиллер, входили в число претендентов уже давно, но получили Нобелевскую премию только через пять лет после очередного финансового кризиса, вызванного, в частности, неверной оценкой активов со стороны инвесторов.

Полистал работы этих именитых финансистов и…………………….

Чем они отличаются, например от

Жижилев В.И. —  Оптимальные стратегии извлечения прибыли на рынке FOREX и рынке ценных бумаг

Везде  одно и то же

«Если захотеть большего и перейти от описания экономических явлений к их анализу, а затем и синтезу инвестиционных стратегий, то другого пути, кроме, как построение математических моделей, не существует.

Если же осознана сама необходимость построения моделей, в нашем случае – это моделей для решения задачи извлечения прибыли, то остается открытым вопрос – как надо это делать.»

«На сегодня общепринято считать, что курсы обращающихся на рынке финансовых инструментов являются случайными событиями. При рассмотрении указанных событий во времени они образуют случайную последовательность или, что тоже самое, дискретный случайный процесс. Почему курсы тех или иных инструментов ведут себя в данный момент времени так, а не иначе, невозможно объяснить с помощью какой-либо детерминированной теории. Единственный выход из этой ситуации – это статистическое рассмотрение всех рыночных событий.»

И дальше – понеслось по «накатанной»

Математическая модель финансового рынка может быть представлена в виде векторно-матричного дифференциального уравнения вида:

которое может быть решено при начальном условии:

где:

-              вектор X размерности (Nxl) по терминологии, принятой в теории управления динамическими системами, описывает «состояние» динамической системы и в этом смысле может быть назван вектором состояния финансового рынка;

-              матрица коэффициентов А дифференциального уравнения (7.3.5) имеет размерность (NxN);

-              матрица коэффициентов В имеет размерность (NxN), и её структура и значения коэффициентов выбираются таким образом, чтобы обеспечить условие астатизма воспроизведения векторной функции mx(t);

mx(t) – векторная функция, соответствующая математическому ожиданию векторного случайного процесса X(t);

V(t) – векторный случайный процесс белого шума (т. е. некоррелированный случайный процесс, имеющий корреляционную функцию в виде дельта-функции Дирака) с математическим ожиданием, равным нулю.

И тд и тп

Понятия эффективности (доходности) финансовых инструментов является базовым, и оно должно вводиться для любых инструментов, обращающихся на том или ином рынке. Формула для оценки эффективности, как отмечалось ранее, имеет вид:

Возникает закономерный вопрос

Какой именно интервал времени  следует учитывать при решении этого уравнения, а самое главное – от какой точки отсчета следует отталкиваться?

Например

Что бы получить цикличность с завидной постоянностью. как во времени построения фрактала, так и в его волатильности, использовать экстремум цены – бессмысленно!

Далее

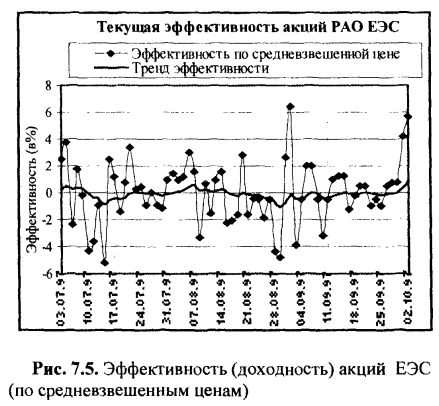
«Решение. На рис. 7.5 приведены реализации случайного процесса эффективности (по средневзвешенным ценам) для акций РАО ЕЭС и, соответственно, тренд эффективности (функция математического ожидания эффективности).»

Векторно-матричное разностное уравнение, описывающее процесс функционирования финансового рынка в дискретном времени с учётом результатов раздела 7.2.2 может быть представлено в виде

Разностное уравнение для ковариационной матрицы векторной случайной последовательности, описываемой уравнением (7.3.36), будет иметь вид:

где P(i) – ковариационная матрица случайного процесса X[i] имеет размерность (NxN), при этом остальные обозначения в уравнении (7.3.37) аналогичны обозначениям для уравнения (7.3.36).

а что если»- убрать фактор « случайного процесса»

и

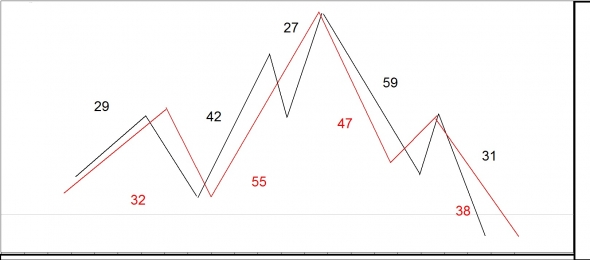
Рассмотрим график в виде работы смешанной модели (REML).

Как  пример используем тикеры товарного и валютного рынков.

Можно добавить и акции и индексы, но нет смысла.  И построения и волатильность и время формирования  будут одни и тоже.

И так

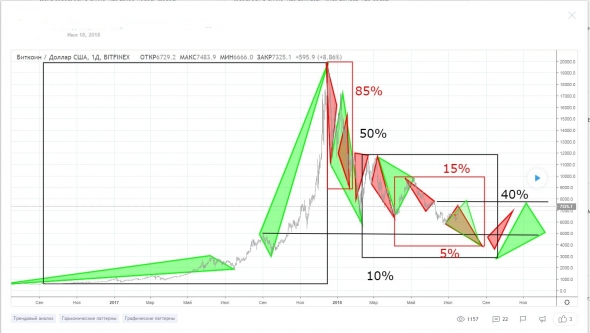
 Цикличность построения товарного тикера


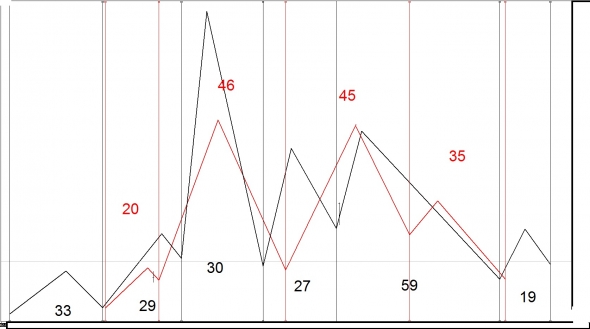
 Цикличность построения валютного тикера

Одна и та же последовательность и структура

«обедним» промежуточные построения в единое целое и получим — идеальное соотношение,  когда товарный и валютный  рынки выходят в одну и туже точку во времени, которая является «отправной» для возникновения – кризисной ситуации на всех рынках



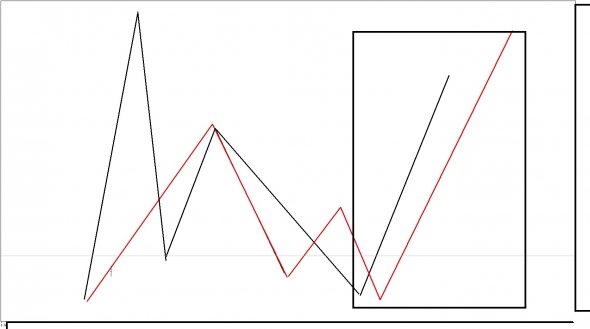
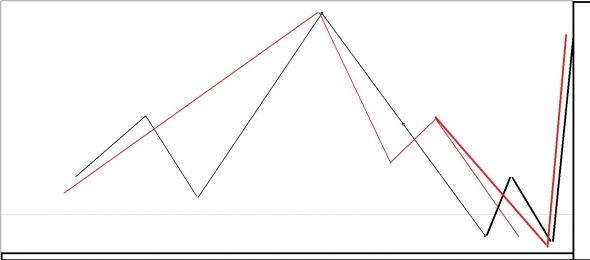
И  в обоих случаях получаем – одну и туже «модель» рыночного поведения

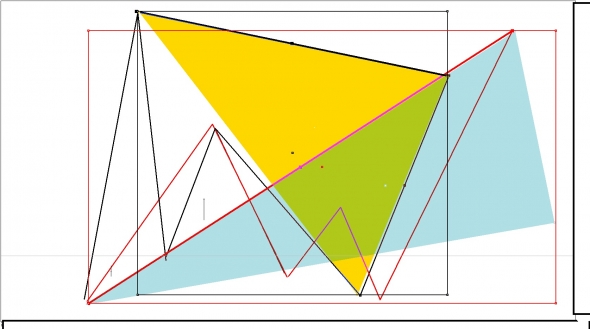
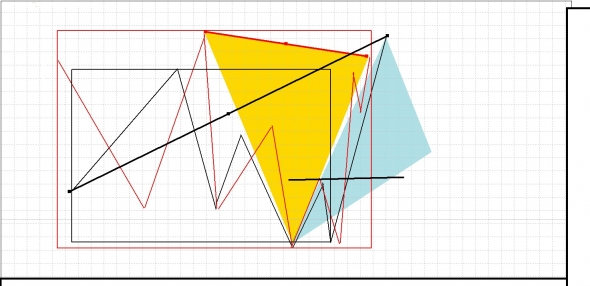
Что это означает,

 уже сейчас с погрешностью 3-5 единиц временного интервала можно назвать время как входа рыночных инструментов в кризисное построение модели, так и выход из нее как во времени, так и в волатильности.

Сколько именно и как именно будут вести себя и первая и вторая волны кризисной ситуации их продолжительность и волатильность, ну и соответственно, как именно будет выходить конкретный тикер из состояния кризиса., а просчитать последующие построение его «ценового коридора» – вообще ни какого труда не составит.

Имеют ли в данном случае как точки отсчета – экстремум цены – однозначно нет! И это конкретные экстремум ни имеющие к развитию модели ни какого отношения, но они будут учитываться при расчете работы по «устоявшимся» рыночным алгоритмам

На рынке работа смешанной  модели (REML) основана совершенно по иному принципу, где Экстремум цены имеет – вторичную роль и может вообще не учитываться в основном ее построении, поскольку выполняет вторичную функцию работая в рамках – промежуточных построений.

Таким образом, если найти  реальную точку отсчета, то цикличность построений любого биржевого, товарного, валютного  тикеров приобретают и одинаковое кол –во  построений как основных, так и промежуточных фракталов, так же низменной становиться и их рабочая  волатильность

В этом легко можно убедиться хотя бы на этих примерах

прогноз

Реализация прогноза 

Другой прогноз


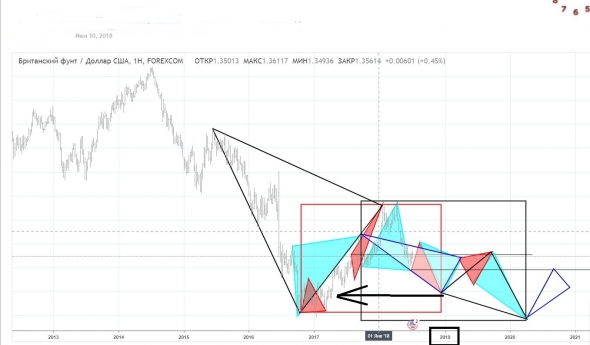
И его реализация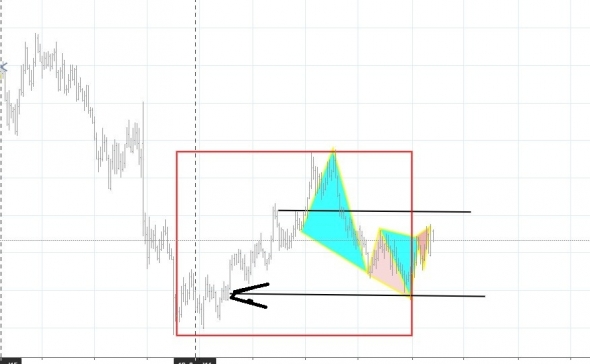

Даже не пытайтесь «вычислить» точки отсчета – все увиденные вами треугольники построены от «балды»

Главное было показать-

— кол-во оставшихся циклов и их допустимую волатильность при формировании конкретного фрагмента ценовой модели.

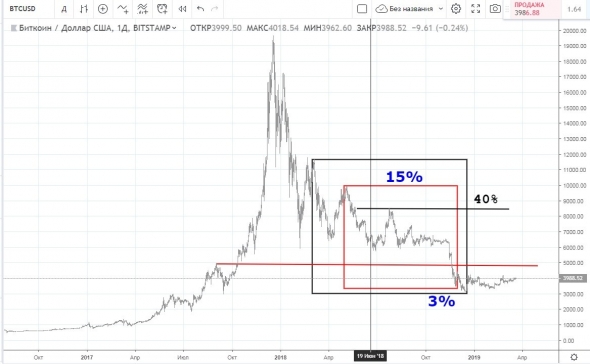
В первом случае

 исключительно из за того что,  «вторичная» модель  забрала на себя функции «основной»,  вместо 5% соотношения получили в итоге  3% соотношение в разнице волатильности  этих моделей

И ошибка в цели  составила 1%

Во втором случае

отработка цели идеальны  как во времени, так и в волатильности,

что сейчас произойдет? – поменяется «прогнозируемое» ранее развитие очередных фрагментов модели, но при этом и время их формирования и волатильность останутся неизменными как и 40 и 20,  так и 5 лет назад.

И данные процессы неизменны для всех инструментов, которые торгуются на любых рынках и на любых интервалах времени.

Таким образом

Изменив  ковариационная матрицу

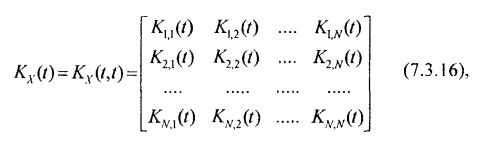
Получим – четкую математическую рыночную модель

Что для этого нужно

— описать численный метод расчета параметров смешанной модели (REML).

— описать метод вычисления ковариационной матрицы смешанной модели

— валидировать с помощью SAS на заранее определенных дата сетах.

— сделать его понятным  для реализации программистом без высшего математического образования.

Итог -

Ликвидности на рынке – придет полный – звиздец!

Нобелевские лауреаты типа Юджин Фама, (Eugene F. Fama), Ларс Петер Хансен (Lars Peter Hansen) и Роберт Шиллер (Robert J. Shiller). –нервно курят в сторонке по простой причине  — данная модель работает  на любом рынке и позволяет прогнозировать развитие рыночного ценообразования на любом интервале времени от тика до десятилетий.

И очень жаль, что,  Владимир Иванович Жижилев в возрасте творческого расцвета скончался от онкологического заболевания.

Я в математике ни  буб – бум, а заниматься с репетитором – это как минимум год, полтора потратить на эту ерунду.

На фига мне это надо?

Обрушить рынки полностью лишив их ликвидности по любому тикеру, наглядно доказать что весь мир торгует  супротив банального алгоритма и никакие объёмы, новости и прочая лабуда не влияют на развитие рыночной модели и  работают исключительно в рамках ее формирования?

Не думаю, что кто то – заслуживает такого  подарка!

Вообще интересно наблюдать за «новостной» фон во время формирования рыночной модели, то кого то арестуют и трубят об этом на весь мир, то кто то помрет «случайно», то в твитерах что то – напишут, когда ждёшь «выстрела» — обязательно какой то «нежданчик» прилетает и так далее, со всеми – вытекающими.

Можно поработать с « математиком», но где найти такого, кто реально бы осознавал – что  именно он получит в  свои руки.

Вот это реально — БОООЛЬшая проблема!