Пересечение скользяшек неинтересно
Модеры, перенесите в алго пжл и вообще добавьте меня уже туда )
Хотелось бы раз и навсегда закрыть тему концепции построения торговых систем или их примеров на основе пересечения скользящих средних. Это не работает, друзья. Давайте посмотрим.
Предположим, для каждого момента времени мы вычисляем значения экспоненциальных скользящих средних (они лучше всех) с периодами А и Э. И также мы знаем приращение цены (или логарифма отношения следующей цены и текущей для упоротых квантов), которое мы можем этой паре чиселок сопоставить. Наносим на график и смотрим:
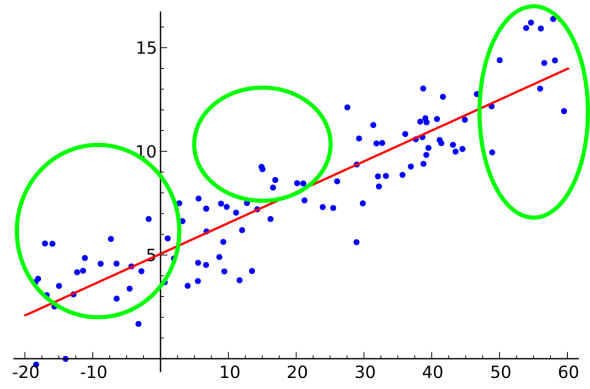
По горизонтальной оси — значения скользяшек с периодом А, по вертикальной — с периодом Э. Если пересекается вверх и находится сверху — оно выше красной линии, наоборот — ниже.
Это просто иллюстрация из Википедии, с нарисованной прямой линией, может быть и другая чуть более сложная кривая-поверхность в случае многих скользяшек и более запутанных правил, суть от этого не меняется. По одну сторону одни точки, предположительно в среднем в плюс, по другую — ну как минимум не такие крутые. Ребята, рынок не так прост ) и одного даже самого хитро%;№"_ного сплита недостаточно от слова совсем.
Попробуйте сами! На самом деле, даже на одной скользяшке можно найти статистически значимую разницу между двумя выборками, которые она порождает. О том, как это считать я писал в одном из предыдущих постов. Но там настолько маленькое преимущество, что его будет невозможно скучно торговать, даже при отрицательной комиссии. Надо улучшать модель. Два сплита — ну посмотрите сами сколько там нужно, три? десять? чтобы хоть немного обозначить островок стабильности в гиперпространстве хаоса ха ха ха.
Короче, резюмируя: численные значения скользяшек могут давать хороший годный сигнал, но они будут при этом находиться внутри какого-то эллипса на графике выше. Разбивая плоскость тупо на две части вы его никогда не найдёте, потому что кроме него шум, этого шума гораздо больше. Если эллипсов два или три, измерений тысяча, всё становится немного сложнее.
Резюме в квадрате — у матожидания системы есть доверительный интервал ) его тоже котируется считать! Дисперсия, всё такое!
P.S. Дорисовал зелёных эллипсов )
пиши еще!
Вернул цвет как было… Белый режет глаза, но что поделать? Серый фон в windows отменили много лет назад. Пусть люди жгут глаза горящим белым! Даёшь зайчики в глаза! =)
Я так туп, что даже вывод понять не смог)
P.S. Слово «простой» у меня не означает SMA.
Пересечение МА — это не способ предсказания приращения цены, а способ открытия/закрытия позиции.
Поэтому сопоставлять его надо не с приращением цены, а с суммой приращений за все время нахождения в позиции, т.е. с куском Эквити.
Расчеты будут сложнее, зато и выводы другие.
С уважением
Допустим. Что тогда нарисовано на картинке?
С уважением
А смотреть нужно не на на один шаг, а вплоть до будущего закрытия по обратному пересечению скользящих.
С увжением
Ну так поясните. Пожалуйста!
Я правда не понимаю, как можно кучу параметров (длины скользящих средних, их значения, оценки матожидания и дисперсии Эквити) запихать в двумерную точечную диаграмму с точками одного цвета.
Вот гляжу я на диаграмму и вижу синюю точку (А, Э)=(-1,7). В левом эллипсе, выше красной линии. Поскольку А<Э, вторая скользящая пересекла первую и вышла вверх. Ну Ок. Но рядом я вижу точку (А, Э)=(-1, 4) ниже красной линии, хотя по-прежнему А<Э. Как это может быть?
Какое приращение показала цена после этого пересечения? Насколько подросло мое Эквити после этого пересечения вплоть до закрытия?
Поймите правильно, тема весьма интересна для дискуссии. МА действительно не работают на длинной дистанции, но доказательство этого факта весьма нетривиально. И одной картинкой здесь не отделаться.
С уважением
А анализ такого рода.
Пусть есть Э1 и Э2, две скользяшки. Для любой точки определяем соотношение Э1-Э2>0 vs <=0. Для каждой точки определяем приращение на следующем такте. Если ровно 10 точек подряд ложатся на одну руку(одинаковое условие), значит 10 одноточечных приращений в сумме дают то, что обычно считают финансовым результатом сделки, за исключением транзакционных издержек, которые в данном анализе игнорируются. Не все ли равно, один раз посчитать 10 движений или 10 раз по одному?
Если не учитывать транзакционные издержки и цели анализа — без разницы.
Обычно все анализируют системы, при этом непонятно, насколько преимущество имеет подгонка, насколько результат системы отражает существенные свойства данных. Поэтому прямой анализ данных, без учета группировок и издержек, имеет смысл именно поиска первичного стат. преимущества, а не способа его использования.
SergeyJu, уважаемый
Понял. Именно с этим я и не согласен. Точное время нахождения в позиции нам неизвестно, среднее — тоже (зависит от Э1 и Э2).
Так что считать надо не 1 приращение и не 10, а финрез нахождения в позиции до отмены (когда Э1-Э2 станет меньше 0), т.е. аккуратно складывать все последующие приращения.
Расчеты и картинка при этом будут посложнее.
С уважением
P.S. Если индикатор Э1-Э2 использовать для прогнозирования матожидания следующего приращения цены, то всегда получим МО будущего приращения = 0
P.S. Насчет равенства нулю МО Вы, в среднем, ошибаетесь. Но, если предположить, что Вы правы, то никакая система на паре скользяшек не несла бы денег — только косты в минус, пропорционально числу сделок.
Не совсем так.
Среднее следующего приращения статистически неотличимо от нуля.
Но это не означает, что результат нахождения в позиции (до обратного пересечения МА) также нулевой. Ибо соседние приращения цен кореллированы, причем неплохо.
С уважением
На самом деле, и в том, и в другом можно обнаружить некоторый (слабый) сдвиг МО. Почему, собственно, мало кому удается извлечь пользу из нейронных сетей на фондовом рынке? МО очень маленькое, а нестационарность и просто шум — велики.
Что это ???
Для пущей загадочности после каждго предложения автору нужно ставить многоточия.
«Скользяшки»?
Вам сколько лет, девушка?
Улучшил. Дальше что?
Предположим в поведении цены есть явление «смена направления». Пусть идеальный индикатор без запаздывания предсказал бы лонг на как минимум ближайшие полчаса.
Пусть по статистике такие лонги подымаются в среднем на рубль.
Комиссия при этом 0,2 рубля на пару взаимнообратных сделок.
Проблема скользящих средних — большое запаздывание. СС покажут этот лонг через 20 минут после «идеального индикатора». Когда лонг отработается уже на 0,75 рубля. Все по-прежнему в среднем.
Вам останется в лучшем случае 0,05 рубля. Если успеете.
Зайдя в соседний подъезд с СС, который неприметен, но несложен, мне удалось сократить запаздывание вдвое.
MS, кажется вы где-то обманываете сами себя. Скользящее среднее «запаздывает» только потому, что оно не учитывает значения цены в будущем. Левая часть графика относительно текущего момента времени «закрыта» же ведь, не так ли? Если бы мы могли подсматривать в будущее за графиком цены, никакие индикаторы вообще были бы не нужны.
Скользяшка — это просто число в определённый момент времени, оно само по себе, просто есть, не запаздывает и ничего не предсказывает. Предсказательной способностью может обладать только модель, в которую это число подаётся как входной параметр.
Но оно может быть разной формы и длительности, у ЭСС — бесконечное (в пределе). Разность двух скользяшек — некий аналог взвешенной оценки производной. Иногда делают скользяшку с инерционным прогнозом. На эталонных временных рядах будет уменьшаться задержка. В теории. На практике увеличивается инерция, как следствие, задержка становится то больше, то меньше.