09 января 2019, 18:30
Хитрая волатильность фьючерса
Что-то притих наш опционный курятник. Давайте немного поразжигаем!
Уверен, что почти все уважающие себя опционщики здесь знают наше любимое уравнение Блэка-Шоулза:
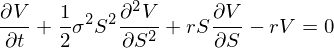
где V — стоимость опциона, S — цена акции, сигма — волатильность акции, r — безрисковая ставка
Также думаю, многие из них знают уравнение Блэка для стоимости опциона на фьючерс. Ведь по идее это оно должно быть нашим любимым на ММВБ, где мы торгуем именно такие опционы:
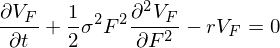
Где Vf — стоимость опциона на фьюч, F — цена фьюча, сигма — волатильность, r — безрисковая ставка
Вроде все красиво и понятно… но почему уравнение Блэка так отличается? Следите за руками:
Мы знаем, что из-за принципа безарбитражности, цена фьючерса жестко связана с ценой акции
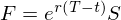
где T — время экспирации фьюча.
Будем искать решение исходного уравнения Блэка-Шоулза в виде
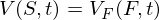
После замены переменных в исходном уравнении получаем:
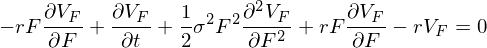
и в итоге приходим к уравнению Блэка:
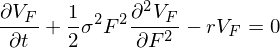
Внимание вопрос: а что это за сигма у нас в уравнении Блэка? Это волатильность чего? Правильный ответ должен привести к некоторому разрыву шаблонов :)
Уверен, что почти все уважающие себя опционщики здесь знают наше любимое уравнение Блэка-Шоулза:
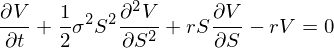
где V — стоимость опциона, S — цена акции, сигма — волатильность акции, r — безрисковая ставка
Также думаю, многие из них знают уравнение Блэка для стоимости опциона на фьючерс. Ведь по идее это оно должно быть нашим любимым на ММВБ, где мы торгуем именно такие опционы:
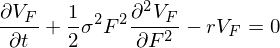
Где Vf — стоимость опциона на фьюч, F — цена фьюча, сигма — волатильность, r — безрисковая ставка
Вроде все красиво и понятно… но почему уравнение Блэка так отличается? Следите за руками:
Мы знаем, что из-за принципа безарбитражности, цена фьючерса жестко связана с ценой акции
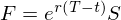
где T — время экспирации фьюча.
Будем искать решение исходного уравнения Блэка-Шоулза в виде
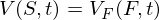
После замены переменных в исходном уравнении получаем:
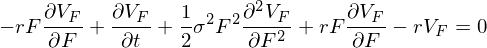
и в итоге приходим к уравнению Блэка:
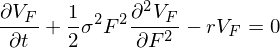
Внимание вопрос: а что это за сигма у нас в уравнении Блэка? Это волатильность чего? Правильный ответ должен привести к некоторому разрыву шаблонов :)
Читайте на SMART-LAB:

XAU/USD: геополитическая премия была растеряна под давлением USD
Золото почти весь прошедший период провело в попытках восстановить понесенные потери после резкой коррекции, но так и не смогло перебить свой максимум, растеряв большую часть прироста....
06.03.2026
💼 Хэдхантер: дивиденды съедают проценты
Крупнейшая онлайн-платформа по поиску работы отчиталась по МСФО за 4 квартал и весь прошлый год Хэдхантер (HEAD) ➡️ Инфо и показатели Результаты за 4 квартал — выручка: ₽10,4...
06.03.2026

💻 Хватит гуглить про недопустимые события
Мы часто говорим о недопустимых событиях. Только в этом канале упоминали их в 42 (!) постах за последние несколько лет. И каждый раз старались объяснить вам, что это такое. Например, как-то...
06.03.2026

Нефтяной срез: выпуск №8. Перекрытие Ормузского пролива + рост цен на нефть против слабых отчетов за 4-й квартал 2025 и 1-й квартал 2026? Ищем лучших в все еще слабом секторе
Продолжаю выпускать рубрику — Нефтяной срез. Цель: отслеживать важные бенчмарки в нефтяной отрасли, чтобы понимать куда дует ветер. Прошлый пост: smart-lab.ru/mobile/topic/1229385/
Почему...
05.03.2026










У нас еще и ставка r обычно равна 0…
Как говорится: "В военное время значение ПИ может достигать 4."
По сути вопроса:
если Вы просто формально подставили V = V(F(S),t) в первое уравнение и далее также формально дифференцировали, то константный параметр sigma, очевидно, все еще остается волатильностью акции.
Кстати, в этой связи возникает логичный вопрос(ы):
— отличается ли волатильность фьючерса от волатильности акции (Базового Актива)?
— Если отличается, можно ли на этом заработать?
— Как? (ответ на последний вопрос логично обсуждать в личке =D )