05 декабря 2018, 14:22
Визуализируя нестационарную нормальность
А. Г. подкинул хорошие мысли, я их немного помонтекарлил. Действительно, модели типа n(a;s) для приращений, где n() — нормальное распределение, а a и s — СВ вполне достаточно, чтобы сгенерирть распределение с тяжелыми хвостами. Чтобы получить восстановленный ряд, похожий по ключевым феноменам на ценовые графики, достаточно простейших модификаций. Например, такая модель:
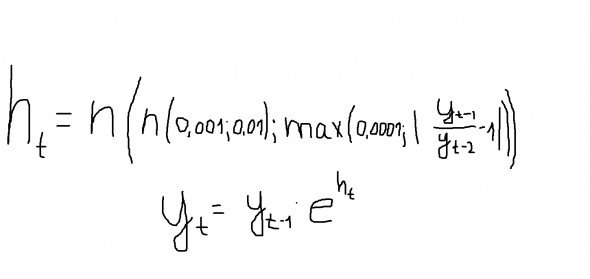
О воспроизведении каких феноменов идет речь? Это гэпы и шпили. 4 случайные реализации подряд:
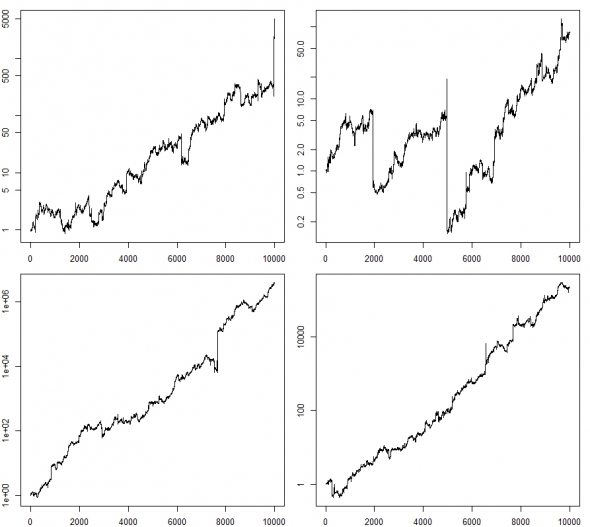
На всякий случай код данной генерации в R:
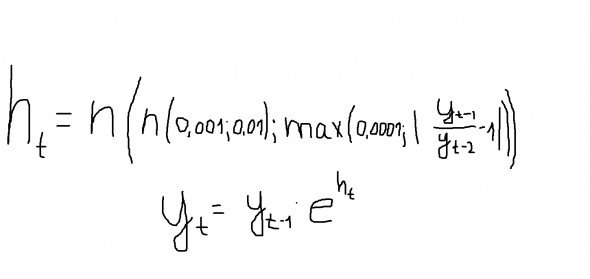
О воспроизведении каких феноменов идет речь? Это гэпы и шпили. 4 случайные реализации подряд:
На всякий случай код данной генерации в R:
N<-10000
y<-array(1,dim=N)
for(n in 2:N)
{
s<-runif(1,0.01,0.01)
a<-rnorm(1,0.001,0.01)
if(n>2) s<-max(abs(y[n-1]/y[n-2]-1),0.001)
y[n]<-y[n-1]*exp(rnorm(1,a,s))
}
plot(y,type="l",log="y")В общем все ключевые ценовые феномены (толстые хвосты, гэпы, шпили) легко воспроизводятся при помощи нестационарной нормальности, которая, напоминаю, путем нормировки на локальную волатильность, легко приводится к стационарной нормальности.
Sloikin, вообще интересно. чем новее (или менее активен) пользователь — тем чаще он дичь какую то на форумах пишет
22:32
Мартын Тимофеев, хотелось бы побыстрее и так они уже последние из магикан…
Курок Плотный, просто смотрим за ситуацией и пользуемся моментом, с этим трубопроводом может произойти все что угодно.
Привет братство — Синий Аллигатор сменяет Зеленого Аллигатора, начинаем через 3 минуты
Donbass, не рано? там же гэп
Не только ВТБ, ГПБ тоже тянет постоянно
GTO, Есть МСФО за 1-ый квартал 2024
РСБУ 24,4 ярда
МСФО 31,7 ярда
Разница 30%
Т. Е. Как и в прошлые годы МСФО больше РСБУ на 25-30%
Если найдете ошибку в моих выкладках буду благодарен. ...
Экспорт зерна и продуктов его переработки превысил 83,5 млн тонн по состоянию на 15 декабря - Россельхознадзор Экспорт зерна и продуктов его переработки превысил 83,5 млн тонн по состоянию на 15 декаб...
Экспорт зерна и продуктов его переработки превысил 83,5 млн тонн по состоянию на 15 декабря - Россельхознадзор Экспорт зерна и продуктов его переработки превысил 83,5 млн тонн по состоянию на 15 декаб...
Коммунизму не бывать!, он тебя обманывал.
Как это моделировать — дело техники.
Я навскидку с десяток альтернативных приведенному способов накидал. Этот — самый топорный, но уже что-то дающий.
Красотишшша! Пытаюсь выучить наизусть, чтобы блеснуть ГДЕ НАДО. Пока не получается...
Он меня забанил и ЧС снёс. Убогий он, ей Богу...
Но он не одинок — ибо их есть у меня, таких убогеньких-то...
Он просто создан для формУ'л. Четырёхэтажных, со степенями и корнями…
Все свои статьи детства, многоформульные, писал в нём. А писА'л про рентгеновскую томографию — там их дохера было, формУ'л-то ентих… С апостерами и даунпостерами… И 4-х этажные дроби...
НИ ПУХА, Друг!
Я свой дисер писал в опенофисе, там был прикольный редактор формул с автоматической нумерацией и тд. Тех тогда не осилил, много телодвижений с ним как мне на тот момент показалось.
И графики рисовать.
И еще пиццу готовит и девок вызванивает.
Московский Лоссбой, и еще цитата из Вики:
1) Принудительные маржинколы
2) Ошибки трейдеров в заявках
3) Массовые стопы
И все это в следствии отсутствия требуемой ликвидности в моменте.
Непонятно зачем непонятным способом мерять «локальную волатильность», чтобы потом получить «стационарный ряд непойми чего».
Если у Вас уже сразу есть в руках готовое распределение. Или как минимум рецепт для моделирования облака траекторий (то бишь вычисления методом Монте-Карло).
Локальную волатильность достаточно померить любым из простых способов (например, СКО последних приращений) при любом фиксированном окне, чтобы получить данный результат. Зачем это нужно? Если не нужно, то не нужно. Как минимум, проделав это, мы понимаем, что в координатах приведенной волатильности перед нами Гаусс, чтоб его так.....
Без моделей мы всё же не можем. А этот факт говорит нам, что с точки зрения моделей порождение нашего процесса вызвано нестационарным Гауссом. Из всего, что в русскоязычной литературе на тему рынка мне удалось прочитать, мне ближе всего то, что говорит А. Г.
Т.е. модель такая. Есть этакий плавающий или нечеткий Гаусс, который то расширяется, то сужается (в модели) и генерит нам поток приращений, из которых мы собираем эмпирическое распределение с известными отклонениями от нормального в виде эксцесса, тяжелых хвостов и тд.
Поскольку без моделей мы не можем, то вот мы и получаем достаточное обобщение — плавающий нечеткий Гаусс или нестационарный Гаусс. Это с точки зрения моделей приращений. Эта модель отвечает нам на два модельных требования: модель для понимания процесса и модель для практики торговли на этом процессе. Здорово же?:)
У меня и другой интерес в этом контексте. Смотреть на это с точки зрения траекторий цен, а не приращений. Что первично это отдельный вопрос. Тут модель по соотношению контртренд/тренд. Пытаюсь увязать (хотя бы на уровне понимания) воедино это с нестационарным Гауссом.