Обещанный Манн-Уитни

Как и обещал в комментарии из моего предыдущего топика

smart-lab.ru/blog/499678.php#comment8969912

Исходные данные: закрытия дня с 07.12.2005 по 16.10.2018 для S&P500 и индекса Мосбиржи

VAR00003, если VAR00004=0: центрированные и нормированные приращения логарифмов индекса Мосбиржи
VAR00003, если VAR00004=1: центрированные и нормированные приращения логарифмов индекса S&P500

Результат

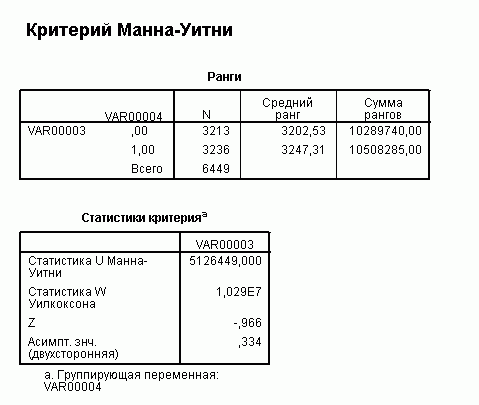
Итого: вероятность ошибиться, утверждая, что эти распределения разные, больше 0,334.

И вывод: выборочные распределения приращений логарифмов дневных значений индексов Мосбиржи и S&P500, вероятней всего, совпадают с точностью до среднего и дисперсии.

S&P500 Индекс ММВБ

howtotradeag

А. Г.

Москва

1702

78 230

с 17 января 2011

25 Комментариев

KarL$oH
17 октября 2018, 13:35
Опять же, страновые риски никто не отменял и эта ваша супер полезная информация не помогла бы вам 09.04.2018 ;)
0
- А. Г.
  17 октября 2018, 13:39
  KiboR, я уже не продавал волатильность 9 апреля, мне хватило 3 марта 2014 А 9 апреля мой результат на счете +0.69%.
  0
  - KarL$oH
    17 октября 2018, 14:03
    А. Г.,
    И вывод: выборочные распределения приращений логарифмов дневных значений индексов Мосбиржи и S&P500, вероятней всего, совпадают с точностью до среднего и дисперсии.
    
    Я про то, что вывод не полит.корректен. 09.04.2018 можно было вляпаться по лонгам мосбиржи, ориентированными, например, на лонги по сиплому.
    0
    - А. Г.
      17 октября 2018, 14:08
      KiboR, Вы уже говорите о кросс-корреляции, а я только об одномерных распределениях.
      0
Sergey Pavlov
17 октября 2018, 13:43
1. Всё же 0,666/0,334=2… в 2 раза это не так уж, чтобы в «одни ворота».
2. Еще было бы интересно сравнить не распределения целиком, а по частям. Отдельно левые хвосты, правые хвосты и серединку.
+1
- А. Г.
  17 октября 2018, 13:50
  Sergey Pavlov, Для критерия вероятность ошибки первого рода больше 0,334 — это очень большая ошибка. Обычно отвергают на уровне 0,1 и даже 0,05. Отвергать гипотезу с 0,334 — это статистический «моветон».
  
  А «хвосты», чтобы мерить, должны содержать по сотне значений. Все там нормально.
  0
  - Sergey Pavlov
    17 октября 2018, 13:58
    А. Г., везде всё нормально:)
    Любопытно, насколько равномерно несовпадение распредлений размазано от левого к правому хвосту. И еще. А какую вероятность ошибки выдаст МУ для сравнения СП500 с нормальным и ММВБ с нормальным?
    +1
    - А. Г.
      17 октября 2018, 14:06
      Sergey Pavlov, да проверял я с нормальным. Нет нормальности ни там, ни там. Но это не опровергает гипотезу, что распределение имеет вид
      
      a+sn, где все три величины случайны, а n — имеет стандартное нормальное распределение.
      
      Более того, я знаю работы, в которых показана близость приращений логарифмов S&P500 и DAX GН распределению, которое является частным случаем распределения случайной величины вышеуказанного вида.
      0
SergeyJu
17 октября 2018, 13:49
Берем торговую систему (без транз.издержек).
Предположим, она более-менее стабильно несет денег на одном индексе и более-менее стабильно сливает на другом. Несмотря на учет разницы в дисперсии. Будет ли это в каком-то смысле доказательством неоднородности двух выборок?
0
- А. Г.
  17 октября 2018, 13:52
  SergeyJu, ничего не доказывает. Любая система «работает» на зависимостях между прошлым и будущим, а я проверял одномерные распределения, которые к зависимостям не имеют никакого отношения.
  0
ch5oh
17 октября 2018, 14:15
"Вероятность ошибиться 33%" — этого недостаточно, чтобы отвергнуть данную гипотезу (гипотезу о том, что "распределения разные").
0
- А. Г.
  17 октября 2018, 14:18
  ch5oh, во-первых, не 0,334, а больше 0,334. Во-вторых, если сиплый разделить пополам по времени, то аналогичная цифра при сравнении половинок составит 0,286.
  0
  - ch5oh
    17 октября 2018, 14:30
    А. Г., собственно, Вы сами написали "отвергать гипотезу при уровне достоверности 30% — статистический моветон".
    
    ПС Проблема, очевидно в том, что у Вас маленькие выборки.
    Но Вас же не интересует чужое мнение.
    Главное, что рынок для Вас просто "нестационарный гаусс".
    0
    - А. Г.
      17 октября 2018, 14:39
      ch5oh, по 3000+ испытаний в каждой выборке совсем немаленькие выборки. Только поправка не «достоверность», а нижняя граница вероятности ошибки первого рода. Достоверность — это другое. Она как раз не меньше 1-0,334.
      0
    - SergeyJu
      17 октября 2018, 14:41
      ch5oh, АГ рассмотрел некую узкую модель и в её рамках сделал выводы. Поскольку модели — налево, торговая практика — направо, констатация того факта, что модель не учитывает некоторые рыночные особенности, имхо, тривиальна.
      0
      - А. Г.
        17 октября 2018, 15:15
        SergeyJu, с точки зрения одномерных распределений она совсем не «узкая», а наоборот очень широкая. Из всего, что я видел, ей противоречит только модель «нормальное в центре, Коши на „хвостах“». То же приближение GH распределением не отвергает модель, а наоборот косвенно подтверждает. В прошлом топике KiBoR свои дипломные результаты приводил, так рассмотренное им распределение — частный случай GH.
        
        Но между одномерными моделями и торговыми практиками, которые могут быть основаны только на временных зависимостях, конечно должен быть «мостик» с дополнительными предположениями, о которых я и не говорил. Из модели можно сделать только пару выводов, которые я собственно и сформулировал в прошлом топике.
        
        А этот топик вообще не о моделях, а о похожести механизмов ценообразования на разных фондовых рынках в разных валютах.
        +1
        SergeyJu
        17 октября 2018, 16:05
        А. Г., человек не смог протиснуться в очень узкую дверцу. Выяснилось, что это самая широкая дверца для кошки во всем городе.
        +1
    - А. Г.
      17 октября 2018, 16:02
      ch5oh, да и не понимаю я, чем Вам «нестационарный Гаусс» не угодил. GH-распределения - «нестационарный Гаусс», и, соответственно, диплом KiBoRa, где рассмотрен частный случай GН-распределения, тоже «нестационарный Гаусс». ARCH-GARCH модели тоже «нестационарный Гаусс». Вон сколько всего под «нестационарный Гаусс» можно подвести.
      0
      - ch5oh
        17 октября 2018, 16:05
        А. Г., именно Ваша конкретная попытка позаниматься пустой схоластикой мне и непонятна.
        
        Собственно, уже примерно раз 20 свои аргументы изложил. Повторяться не вижу смысла.
        0
        А. Г.
        17 октября 2018, 16:07
        ch5oh, ну не совсем пустая. Самоподобие таймфреймов отвергается, вид оптимальных индикаторов определяется. Какая то польза есть. Не густо конечно, до основного — определения зависимости между прошлым и будущим конечно далековато.
        +1
        SergeyJu
        17 октября 2018, 16:33
        А. Г., а мы хотим всего и сразу!
        0
        А. Г.
        17 октября 2018, 16:37
        SergeyJu, да я боюсь, что когда когда начну вводить дополнительные ограничения, то критики тут будет еще больше Поэтому эту часть убрал на ютуб от «греха подальше»
        
        +1
        SergeyJu
        17 октября 2018, 16:41
        А. Г., я заметил, что у меня эмоциональный протест вызывают не Ваши выводы, а Ваши модели. Мне все время хочется крикнуть, что модель-то не настоящая :)
        0
        А. Г.
        17 октября 2018, 16:55
        SergeyJu, ну по крайней мере люди проверяют ее соответствие рынку, не находят противоречий и даже косвенно подтверждают. Мне же просто лень писать программу на проверку соответствия между рынком и GH-распределением. Я просто не вижу на ее выходе ничего «прорывного», кроме чисто академических результатов.
        
        Я может быть слишком завуалировано, но своим прошлым постом хотел донести еще одну мысль, которая наверняка Вам покажется тривиальной: "«тяжелые хвосты» одномерных приращений логарифмов цен не являются доказательством неэффективности рынка, а потому не могут быть «ключом» для построения торговых правил. Более того «тяжелые хвосты» могут быть присущи и абсолютно эффективному рынку".
        
        Мысль действительно тривиальна, но почему то ее отрицание я читаю в интернете из года в год.
        0
        SergeyJu
        17 октября 2018, 17:05
        А. Г., а как же теория «ударных дней»?
        Связи надо искать на рынке, зоны предсказуемости, а не на хвосты надеяться, имхо.
        +2