Статистические модели трендов. Авторегрессивность.

Обещанное продолжение. Предыдущий пост из серии: http://smart-lab.ru/blog/43277.php 

В чем собственно смысл понятия авторегрессивности/автокорреляции/персистентности. Расмотрим простейший процесс в котором последующие приращения зависят от предыдущего. Обозначим приращение в момент времени t — X_t, в момент времени t + 1 — X_t+1. Соответственно мы хотим, чтобы приращение в момент времени t+1, каким то образом зависело от предыдущего t. Если выразить такую зависимость качественно, то у нас есть два варианта.

1) первый вариант, мы предполагаем что положительное приращение X_t должно увеличивать вероятность положительного приращения в следующий момент времени X_t+1, аналогично для  отрицательного. Проще говоря Х_t и X_t+1 положительно скоррелированны. Такая модель является «трендовой, персистентной», то есть покупая/продавая то что растет/падает мы смещаем вероятность выигрыша в свою сторону.

2)  второй вариант, мы предполагаем что положительные приращения X_t должны увеличивать вероятность отрицательных в момент времени X_t+1, а отрицательные приращения — положительных. То есть X_t и X_t+1 отрицательно скоррелированны. Такая моделья является «контр трендовой, анти-персистентной», то есть продавая то что выросло и покупаю то что упало, мы получаем статистическое преимущество. 

Соответственно если закодировать эти наблюдения в виде общей формулы мы получим: X_t+1 = C + A*X_t + W_t, С — это смещение мат ожидания, A — коэффициент авторегрессии, W — белый(к примеру гаусовский) шум. Для простоты предположима что C = 0, тогда при A > 0 получим первый вариант из расмотренных выше, если A < 0 то второй. При A = 1 получаем случайное блуждание, если A по модулю > 1, модель теряет устойчивость, что характеризуется взрывным(экспоненциальным) ростом/падением или расширяющимися колебаниями с экспоненциальным ростом амплитуды. 
Если еще больше расширить модель, то в общем случаи она может зависеть от нескольких значений в предыдущей истории, то есть зависимость будет иметь вид: X_t+1 = C + A1*X_t + A2*X_t-1 + A3*X_t-2 +… + Ai*X_t-i-1, но мы ограничимся расммотрения случая с единичным лагом и C=0 как наиболее характерного.

Теперь рассмотрим как этот простейший пример будет выглядеть. Для этого возьмем исходный гаусовский шум:

 
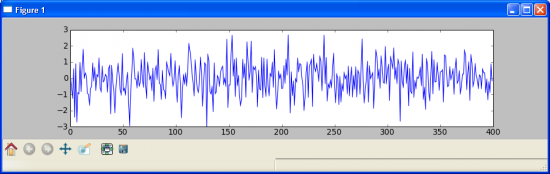
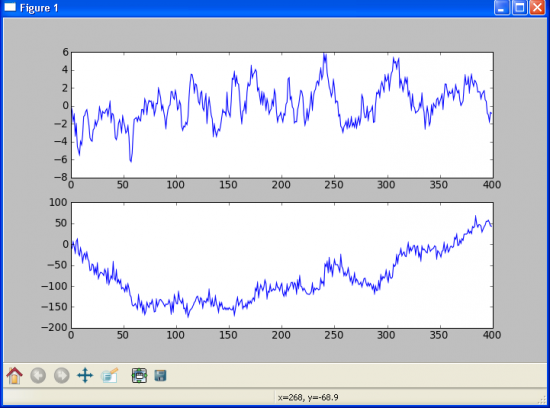
И применим к нему нашу AR(1) (авторегрессивность с 1 лагом) модель, с различными значениями A и C=0. При A=0.9, получим(сверху, результат авторегрессивной модели приращений, снизу интеграл этих приращений + аддативный шум — то есть приближение к случайному блуждания, рыночной модели):
 


Таже самая модель при A=0.15:


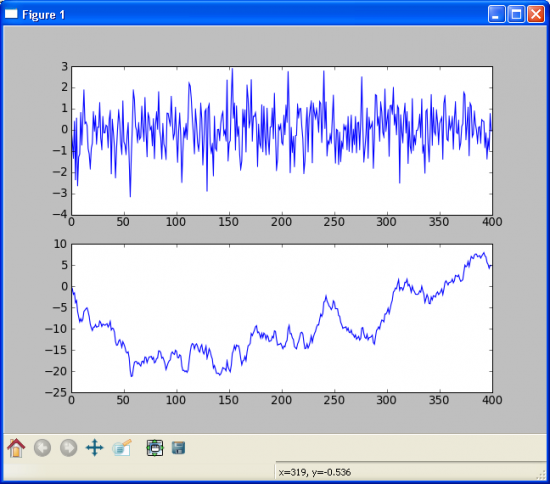
Зависимость слабая, но несмотря на это хорошо видно, как возникают локально-трендовые участки на графике.

Так же если мы построим, облако точек, где по оси X — приращение X_t, а по Y — приращение X_t-1, эта зависимость будет отчетливо видна:
 

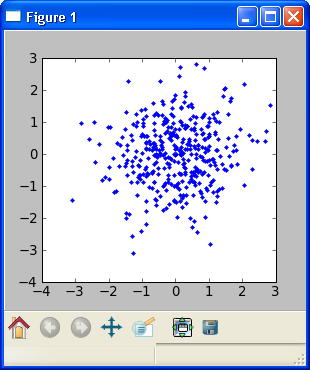
Теперь переходим к оставшейся части. Очевидно что стационарных зависемостей на рынке нет, поэтому автокорреляционная функция приращений имеет тривиальный вид. Из этого следует что такие зависимости могут быть описаны лишь в лучшем случаи, нестационарными моделями, то есть такими в которых вид этой локальной зависимости не остается постоянным а изменяется время от времени. Аналогично, введенной в предыдущем посте «Статистические модели трендов. Смещение среднего.», мы може ввести кусочно постоянную функцию, но на этот раз она будет описывать не смещение среднего, а значение коэфициента регрессии A. Таким образом получить участки на которых авторегрессия носит локально-трендовый характер(A>0), на других — локально-контртрендовый(A<0), чтобы в конечном итоге удовлетворить наше условие тривиальности АКФ.