20 ноября 2017, 12:11
Доходность при регулярных вложениях в боковик
Усреднение--это важная тема в трейдинге. Поэтому дабы иметь некие опорные точки, полезно придумывать простые модели для понимания происходящего. Одной из таких опорных моделей является модель регулярных вложений в боковое движение цены. Общеизвестно, что при регулярном вложении постоянных сумм в среднем не меняющуюся, но колеблющуюся цену будет генерироваться некая доходность. Это связано с тем, что при низкой цене покупается большее количество юнитов, чем при высокой.
В настоящей заметке произведен точный аналитический расчет доходности для модели синусоидального поведения цены. Для зависимости цены от времени принята модель P(t)=P0+P1*sin(b*t). В рамках данной модели в континуальном пределе показано, что доходность на один период движения цены равна половине квадрата отношения амплитуды колебаний цены к ее среднему значению: 0.5*(P1/P0)^2. То есть единицы процентов на период для типичных значений амплитуд колебаний 10-50% на реальном рынке.
Данный результат является почти очевидным, квадратичная зависимость имеет понятный физический смысл. Доходность есть произведение превышения числа дешевых юнитов над числом дорогих юнитов, умноженная на превышение дорогой цены над дешевой. То есть (P1/P0)*(P1/P0). Коэффициент 0.5 без вычислений не угадаешь--но он должен быть порядка единицы, это тоже очевидно. Уж точно этот результат отлично известен в сообществе. Так что это как напоминание, ну и автору хотелось вспомнить матан. А то волчья реальность финансовых рынков однообразна и скучна, чистый полет моделей, интегралов и рядов Тейлора--это ж кайф :)
Подробный расчет с полным брутальным и суровым матаном--на фотографиях. Общее наблюдение по поводу матана в трейдинге--напрямую не нужен, но очень помогает.



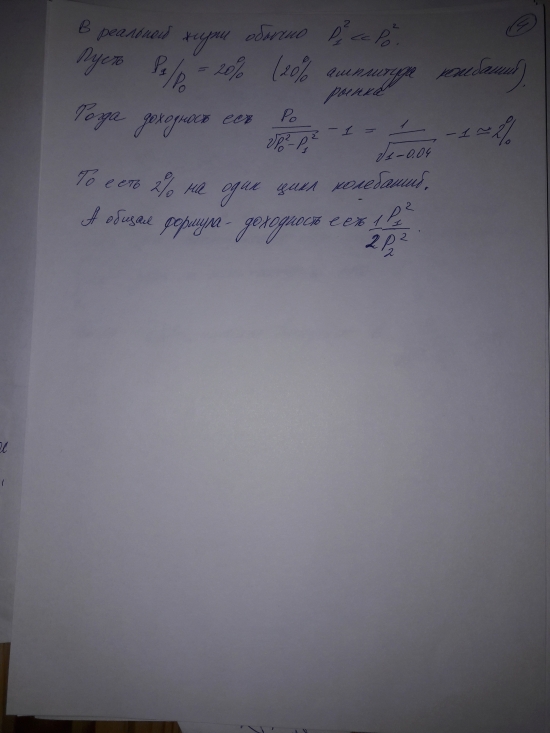
В настоящей заметке произведен точный аналитический расчет доходности для модели синусоидального поведения цены. Для зависимости цены от времени принята модель P(t)=P0+P1*sin(b*t). В рамках данной модели в континуальном пределе показано, что доходность на один период движения цены равна половине квадрата отношения амплитуды колебаний цены к ее среднему значению: 0.5*(P1/P0)^2. То есть единицы процентов на период для типичных значений амплитуд колебаний 10-50% на реальном рынке.
Данный результат является почти очевидным, квадратичная зависимость имеет понятный физический смысл. Доходность есть произведение превышения числа дешевых юнитов над числом дорогих юнитов, умноженная на превышение дорогой цены над дешевой. То есть (P1/P0)*(P1/P0). Коэффициент 0.5 без вычислений не угадаешь--но он должен быть порядка единицы, это тоже очевидно. Уж точно этот результат отлично известен в сообществе. Так что это как напоминание, ну и автору хотелось вспомнить матан. А то волчья реальность финансовых рынков однообразна и скучна, чистый полет моделей, интегралов и рядов Тейлора--это ж кайф :)
Подробный расчет с полным брутальным и суровым матаном--на фотографиях. Общее наблюдение по поводу матана в трейдинге--напрямую не нужен, но очень помогает.



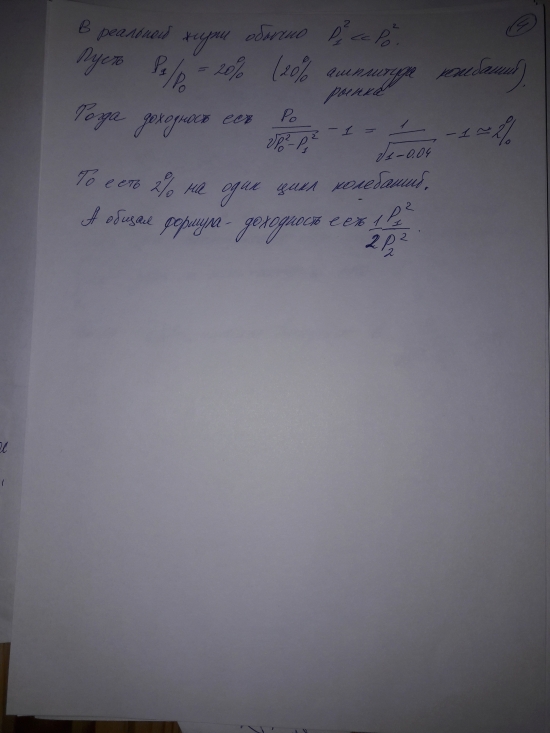
27 Комментариев
 PSH20 ноября 2017, 12:15Особый сюрреалистичный шарм заметке придают кондовые фотки бумажек с рукописным текстом вместо, например, листинга в маткаде :)+1
PSH20 ноября 2017, 12:15Особый сюрреалистичный шарм заметке придают кондовые фотки бумажек с рукописным текстом вместо, например, листинга в маткаде :)+1 Sergey Александрович20 ноября 2017, 12:25Забугорная стратегия, удачная при условии роста актива. Для особого класса инвесторов.0
Sergey Александрович20 ноября 2017, 12:25Забугорная стратегия, удачная при условии роста актива. Для особого класса инвесторов.0
Читайте на SMART-LAB:
🖥 Яндекс выбирает дивиденды
IT-компания отчиталась за 4 квартал и прошлый год Яндекс (YDEX) ➡️ Инфо и показатели Результаты за 4 квартал — выручка: ₽436 млрд (+28%); — скорр. EBITDA: ₽87,8 млрд (+80%);...
17:11

Как заработать на переговорах по Украине: любимые миркоины трейдеров
В преддверии нового раунда переговоров по Украине редакция Т-Инвестиций спросила трейдеров об их ожиданиях, планах и инструментах, с помощью которых они предпочитают отрабатывать новости...
18:33











