Эмпирическое распределение
Интересную тему с эмпирическими распределениям подняли Дмитрий Новиков и Nonsense. Хотелось бы одну мысль по этому поводу озвучить. Насколько понимаю, эмпирическое распределение — это когда берут историю цен БА, нарезают неким окном, из каждого полученного отрезка получают приращение, и потом строят частотную диаграмму из этих приращений. Полученное распределение и называют эмпирическим. Nonsense пишет, что возникают две проблемы:
1. У полученного распределения мю может быть не ноль, и если считать по этому распределению справедливые цены, то не будет выполняться колл-пут паритет.
2. Выбор размера окна для нарезки.
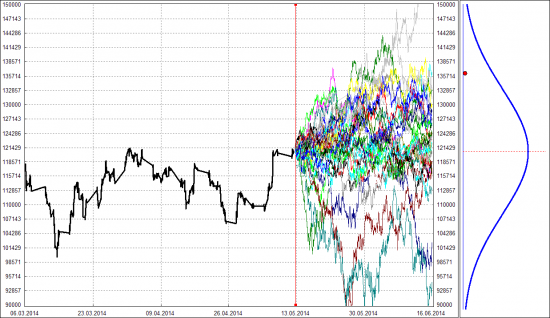
Мне же кажется, что тут другая, более существенная, проблема. Предположим, у нас есть некий случайный процесс, с помощью которого мы можем сгенерировать кучу случайных траекторий цены:
Построив частотную диаграмму финишных точек каждой траектории, мы получим как-бы распределение вероятностей — истинное для нашего случайного процесса. Теперь вопрос: если мы возьмем только одну траекторию и построим из нее эмпирическое распределение, будет ли оно совпадать с истинным распределением? Уверен, что нет.
Анализируя одну такую траекторию может быть и можно частично понять некоторые св-ва исходного случайного процесса (типа, рост волатильности при падении цены), но полностью его расшифровать — мне кажется, невозможно.
И еще соображение. Мы ведь говорим про вероятности. А что это? Так понимаю, есть два подхода: частотный и байесовский. И вроде бы второй подход гораздо точнее прогнозирует (например, тот кто прогнозирует будет сегодня дождь или нет на основе кол-ва дождливых дней в году проиграет тому, кто смотрит ясный сегодня день или пасмурный). Так вот, эмпирическое распределение соответствует частотной вероятности. А рыночное распределение (получаемое из текущих цен опционов на всех страйках) — байесовскому подходу. Например, выходит какая-то важная новость, рыночное распределение на это сразу реагирует и соответствующим образом изменится. А эмпирическое никак на эту новость не отреагирует.
В общем, использовать эмпирическое распределение (для прогноза где будет БА или для подсчета своих справедливых цен), имхо, дюже неправильно.
bstone10 января 2017, 23:18Имелось в виду эмпирическое распределение, построенное по ряду приращений цены.0- bstone10 января 2017, 23:28Но стоит отметить, что такая вот нарезка «окон» является хорошей иллюстрацией свойства эргодичности процессов, описываемых случайным блужданием.0
Кирилл Браулов10 января 2017, 23:35А зачем такое? Оно же не прогнозирует, где будет цена БА на заданную дату? И справедливых цен по нему не посчитаешь. Единственно для чего его имеет смысл построить, чтобы убедиться, что оно отличается от нормального (как предполагается в БШ). У меня для Ri такое отличие получалось:
+1
Старый бес10 января 2017, 23:35Я с Кириллом скорее согласен. В том смысле, что эмпирическое распределение штука, зачастую, не просто бесполезная, но и опасная. Мне достаточно и тех двух причин о которых писал. А про Байесовскую вероятность первый раз слышу(( пойду повышать уровень знаний. Кирилл, спасибо0
