Индикатор фрактальной размерности | LUA

Упрощенный алгоритм вычисления приближенного значения размерности Минковского, для ценового ряда.

Краткая справка:

Размерность Минковского — это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:

• где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.

Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов. 

Более полная и интересная статья

Ну а я применил данный алгоритм, для создания простого индикатора фрактальной размерности


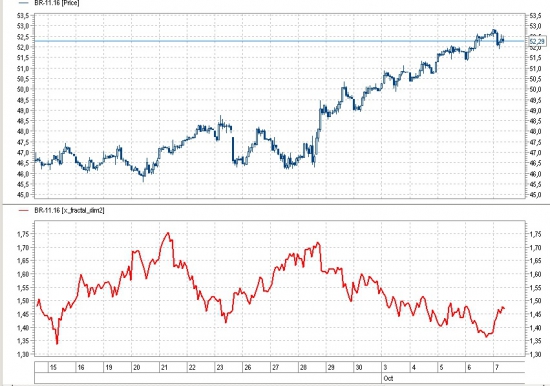
Для чего? — как альтернативный индикатор определения состояния в тренде или во флете.

Для сравнения 

Размерность простой линии = 1
Размерность множества Жулиа (картинка выше) = 1,683
Размерность ценового ряда достигает до 1,8

Ну и сам файл x_fractal_dim2.lua