Измерение информации на рынке с помощью PIN. Часть 2
В прошлой части мы рассмотрели теоретическую модель, лежащую в основе вычисления вероятности присутствия на рынке информированных трейдеров PIN. Продолжим с эмпирической реализации этой модели.
Для уменьшения пространства параметров модели, обычно предполагают, что частоты прихода ордеров на продажу ϵs и на покупку ϵb равны. В день «хорошей новости» вероятность наблюдения последовательности сделок купли и продажи соответствует:
![Измерение информации на рынке с помощью PIN. Часть 2 \exp(-(\mu+\epsilon)T)\frac{[(\mu+\epsilon)T]^B}{B!}\exp(\epsilon T)\frac{(\epsilon T)^S}{S!}](http://mathurl.com/q2uamv5.png) , где B и S — число сделок купли и продажи соответственно.
, где B и S — число сделок купли и продажи соответственно.
Для дней «плохой новости»:
![Измерение информации на рынке с помощью PIN. Часть 2 \exp(\epsilon T)\frac{(\epsilon T)^B}{B!}\exp(-(\mu+\epsilon)T)\frac{[(\mu+\epsilon)T]^S}{S!}](http://mathurl.com/qboxxlc.png)
И для дней с отсутствием новостей вероятность равна:
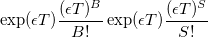
Предполагая, что торговая активность независима от одного дня к другому в течении T дней, вероятность торговой активности принимает форму:
![Измерение информации на рынке с помощью PIN. Часть 2 L[\{B,S\}|\theta]=(1-\alpha)\exp(-\epsilon T)\frac{(\epsilon T)^B}{B!}\exp(-\epsilon T)\frac{(\epsilon T)^S}{S!}](http://mathurl.com/p9v66b6.png)
![Измерение информации на рынке с помощью PIN. Часть 2 +\alpha\delta\exp(-\epsilon T)\frac{(\epsilon T)^B}{B!}\exp(-(\mu+\epsilon)T)\frac{[(\mu+\epsilon)T]^S}{S!}](http://mathurl.com/ocazhrz.png)
![Измерение информации на рынке с помощью PIN. Часть 2 +\alpha(1-\delta)\exp(-(\mu+\epsilon)T)\frac{[(\mu+\epsilon)T]^B}{B!}\exp(-\epsilon T)\frac{(\epsilon T)^S}{S!}](http://mathurl.com/owuv4pc.png)
с пространством параметров θ=α,δ,ϵ,μ. За h независимых дней вероятность наблюдения 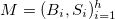 равна произведению дневных вероятностей:
равна произведению дневных вероятностей:
![Измерение информации на рынке с помощью PIN. Часть 2 L[M|\theta]=\prod_{h=1}^h L(\theta|B_i,S_i)](http://mathurl.com/ph5dt7u.png)
Для сходимости при численной максимизации преобразуем функцию вероятности следующим образом:
![Измерение информации на рынке с помощью PIN. Часть 2 L[M|\theta]=\sum_{i=1}^T[-2\epsilon+M_t\ln(x)+(B_t+S_t)\ln(\mu+\epsilon)]](http://mathurl.com/od48bp9.png)
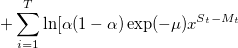
![Измерение информации на рынке с помощью PIN. Часть 2 +\alpha\delta\exp(-\mu)x^{B_t-M_t}+(1-\alpha)x^{B_t+S_t-M_t}]](http://mathurl.com/o36lrrz.png)
где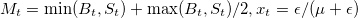
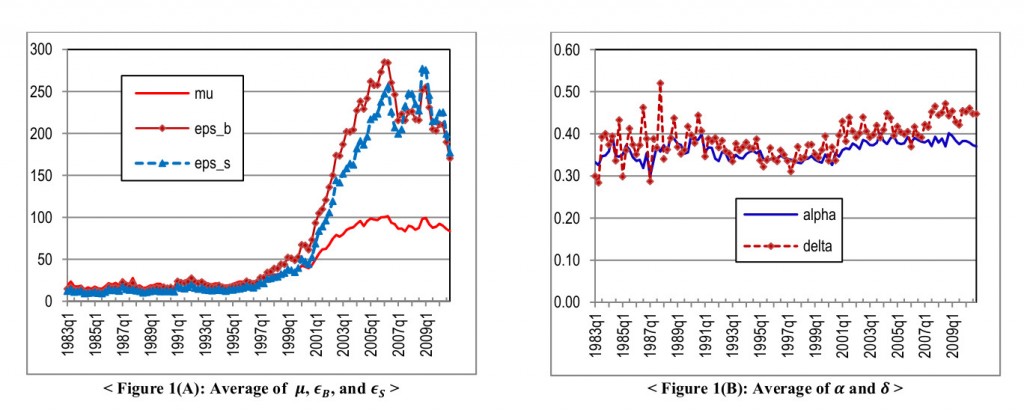
Найти параметры θ можно методом численной максимизации вышеприведенной вероятности (в заглавии поста приведены графики полученных параметров для акций NYSE с 1983 по 2009 год). После этого мы сможем найти индикатор информированной торговли PIN, который равен безусловной вероятности того, что информированные участники покупают или продают актив в каждый момент времени:
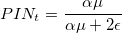
Когда значение PIN велико, неинформированные трейдеры сталкиваются с высоким риском того, что их контрагент в сделках лучше информирован. В своих алгоритмах необходимо учитывать этот индикатор и предпринимать соответствующие действия при его высоком значении, например, снимать ордера, противоположные текущему направлению движения цены.
Пакет PIN языка R содержит функцию для вычисления логарифма вероятности торговой активности. На вход она принимает значения параметров -ϵ,μ,α,δ- и временную последовательность дневных данных с числом сделок купли и продажи, помещенных в матрицу размерностью n х w, где n — число торговых дней. Первая колонка матрицы содержит число сделок купли, вторая — число сделок продажи.
В следующей части мы рассмотрим практический пример с использованием языка R, где применим численную максимизацию упомянутой выше функции и получим значения параметров, а затем, соответственно, вычислим PIN — — продолжение смотрите на моем сайте, или, позднее, на смарт-лабе.
 ololosha09 июня 2015, 13:40почитал предыдущую статью тоже. спасибо, интересно! по-моему проще всего реализовать данную тему на валютах, т.к. большинство новостей на валюте выходят систематично и с фиксированным временем. на метатрейдере даже есть индикаторы, которые на графике указывают время выхода новостей и их показатели относительно ожиданий.0
ololosha09 июня 2015, 13:40почитал предыдущую статью тоже. спасибо, интересно! по-моему проще всего реализовать данную тему на валютах, т.к. большинство новостей на валюте выходят систематично и с фиксированным временем. на метатрейдере даже есть индикаторы, которые на графике указывают время выхода новостей и их показатели относительно ожиданий.0 SciFi09 июня 2015, 15:12Очень хорошо. Большое спасибо за источник.0
SciFi09 июня 2015, 15:12Очень хорошо. Большое спасибо за источник.0