Улыбка волатильности. Модель Бейтса
Продолжение. Начало в моем блоге и на сайте.
В прошлой статье про модель Хестона мы отметили, что она обладет недостатком, который проявляется в неточности определения цен опционов на малых сроках экспирации. Здесь мы рассмотрим модель Бейтса, в которой этот недостаток устранен, и она является одной из лучших аппроксимаций, описывающих поведение цен опционов для разных страйков и периодов до экспирации.
Модель Бейтса относится к моделям стохастической волатильности и определятся следующими уравнениями:
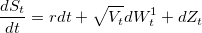
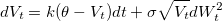
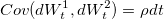
Как видите система уравнений почти идентична хестоновской, с теми же переменными: St, Vt- цена и волатильность базового актива, 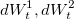 — случайные броуновские процессы с корелляцией, ρ,r,k,θ,σ- параметры модели (r=0 для маржируемых опционов). Разница в появлении слагаемого dZt, которое представляет собой Пуассоновский процесс с интенсивностью λ и лог-нормальным распределением скачков цены, независимым от
— случайные броуновские процессы с корелляцией, ρ,r,k,θ,σ- параметры модели (r=0 для маржируемых опционов). Разница в появлении слагаемого dZt, которое представляет собой Пуассоновский процесс с интенсивностью λ и лог-нормальным распределением скачков цены, независимым от 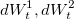 . Таким образом модель Бейтса является расширением модели Хестона с добавлением процесса скачков цены, что позволяет более точно воспроизвести реальный процесс приращения цены базового актива.
. Таким образом модель Бейтса является расширением модели Хестона с добавлением процесса скачков цены, что позволяет более точно воспроизвести реальный процесс приращения цены базового актива.
Если обозначить J размер скачка цены тогда:
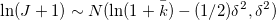 , для некоторого k¯, то есть процесс скачков имеет нормальное распределение со средним
, для некоторого k¯, то есть процесс скачков имеет нормальное распределение со средним 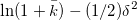 и дисперсией
и дисперсией 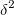 .
.
Тогда логарифимическое приращение цены базового актива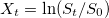 при условии риск-нейтрального подхода можно записать как:
при условии риск-нейтрального подхода можно записать как:
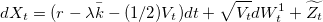
где Zt˜- Пуассоновский процесс с нормальным распределением величины скачков цены.
Для упрощения не буду приводить аналитическую формулу цены колл опциона для модели Бейтса, она схожа с хестоновской, желающие могут посмотреть, например, здесь. Сразу дам листинг вычисления этой цены на C#:
//a-нижний предел интеграла (равен 0)
//b - верхний предел интеграла. Выбирается значение от 100 до 200, в зависимости от нужной точности
//delta - вычисляется грек дельта, который равен значению Р1
double BatesCallGaussLegendre(double S, double K, double T, double r, double kappa, double theta,
double sigma, double lambda, double v0, double rho,
double a, double b, double muJ, double vJ, ref double delta)
{
// Числовое интегрирование
double[] int1 = new double[32];
double[] int2 = new double[32];
double y;
Complex om;
Complex i = new Complex(0.0, 1.0);
Complex Xk = new Complex(K, 0.0);
for (int k = 0; k <= 31; k++)
{
y = (a + b) / 2.0 + (b - a) / 2.0 * X[k];
om = new Complex(y, 0.0);
int1[k] = W[k] * (Complex.Exp(-i * Complex.Log(Xk) * om) * BatesCF(om - i, S, T, r, 0, v0, theta, rho, kappa, sigma, lambda, muJ, vJ) / (i * om * S)).Real;
int2[k] = W[k] * (Complex.Exp(-i * Complex.Log(Xk) * om) * BatesCF(om, S, T, r, 0, v0, theta, rho, kappa, sigma, lambda, muJ, vJ) / (i * om)).Real;
}
// Вектора интегральной суммы
double I1 = VectorSum(int1);
double I2 = VectorSum(int2);
// Определение P1 и P2
double P1 = 0.5 + 1.0 / Math.PI * I1 * (b - a) / 2;
double P2 = 0.5 + 1.0 / Math.PI * I2 * (b - a) / 2;
delta = P1;
// Цена колл опциона
return S * P1 - K * P2;
}
private Complex BatesCF (Complex phi ,double Spot, double T , double Rate, double Divd,double V ,double Theta , double Rho ,double Kappa, double Sigma ,
double Lambda , double MuJ , double VJ)
{
Complex S=new Complex(Spot , 0.0); // Цена базового актива
Complex r=new Complex(Rate , 0.0); // Безрисковая ставка (для маржируемых опционов =0)
Complex tau=new Complex(T , 0.0); // Период до экспирации в долях года
Complex i=new Complex(0.0 , 1.0); // мнимая часть комплексной переменной
Complex rho=new Complex(Rho , 0.0); // Параметр Бейтса: корелляция
Complex k=new Complex(Kappa , 0.0); // Параметр Бейтса: скорость возврата к средней
Complex vT=new Complex(Theta , 0.0); // Параметр Бейтса: уровень возврата
Complex lambda=new Complex(Lambda, 0.0); // Параметр Бейтса: интенсивность скачков
Complex sigma=new Complex(Sigma , 0.0); // Параметр Бейтса: среднеквадратичное отклонение волатильности
Complex v0=new Complex(V , 0.0); // Параметр Бейтса: текущая волатильность
Complex two=new Complex(2.0 , 0.0); // Число 2.0 в комплексной форме
Complex one = new Complex(1.0, 0.0); // Число 1.0 в комплексной форме
Complex muJ=new Complex(MuJ , 0.0); // Параметр Бейтса: средняя скачков ( в тексте k с верхним подчеркиванием)
Complex vJ=new Complex(VJ , 0.0); // Параметр Бейтса: дисперсия скачков
Complex q=new Complex(Divd , 0.0); // дивиденды (для опционов на фьючерсы =0)
Complex d = Complex.Sqrt (Complex.Pow(( rho * sigma * i*phi - k),2) + sigma*sigma * (i*phi + phi * phi));
Complex g2 = (k - rho* sigma *i*phi - d) / (k - rho* sigma *i*phi + d);
Complex cf1 = i*phi * (Complex.Log(S) + (r - q) * tau);
Complex cf2 = vT * k / ( sigma *sigma) * ((k - rho* sigma *i*phi - d) * tau - two * Complex.Log ((one - g2 * Complex.Exp(-d * tau)) / (one - g2)));
Complex cf3 = v0 / sigma *sigma * (k - rho* sigma *i*phi - d) * (one - Complex.Exp(-d * tau)) / (one - g2 * Complex.Exp(-d * tau));
// Составляющая для скачков цены:
Complex cf4 = -lambda*muJ *i*tau*phi + lambda*tau *( Complex.Pow((one+ muJ) ,(i*phi)) * Complex.Exp( vJ *(i*phi /two) * (i*phi -one) ) -one );
Complex cf = Complex.Exp(cf1 + cf2 + cf3 + cf4);
return cf;
}
//Функция суммирования элементов вектора
double VectorSum(double[] A)
{
double sum = 0;
double n = A.Length;
for (int i = 0; i <= n - 1; i++)
sum += A[i];
return sum;
}
Калибровка модели Бейтса аналогична калибровке Хестона, рассмотренной в прошлой статье. Однако в случае Бейтса нужно находить не 5 параметров модели а восемь: k,ρ,θ,σ,Vt,k¯,λ,δ2. Три последних параметра добавились от процесса скачков ( отмечу, что λ, упомянутая в статье о Хестоне имела другой смысл, чем параметр Бейтса — просто совпали обозначения). Это значительно усложняет нахождение глобального минимума и увеличивает время вычисления параметров модели. Здесь скорее всего уже не обойтись без применения алгоритмов поиска глобальных минимумов, типа Differential Evolution или ASA.
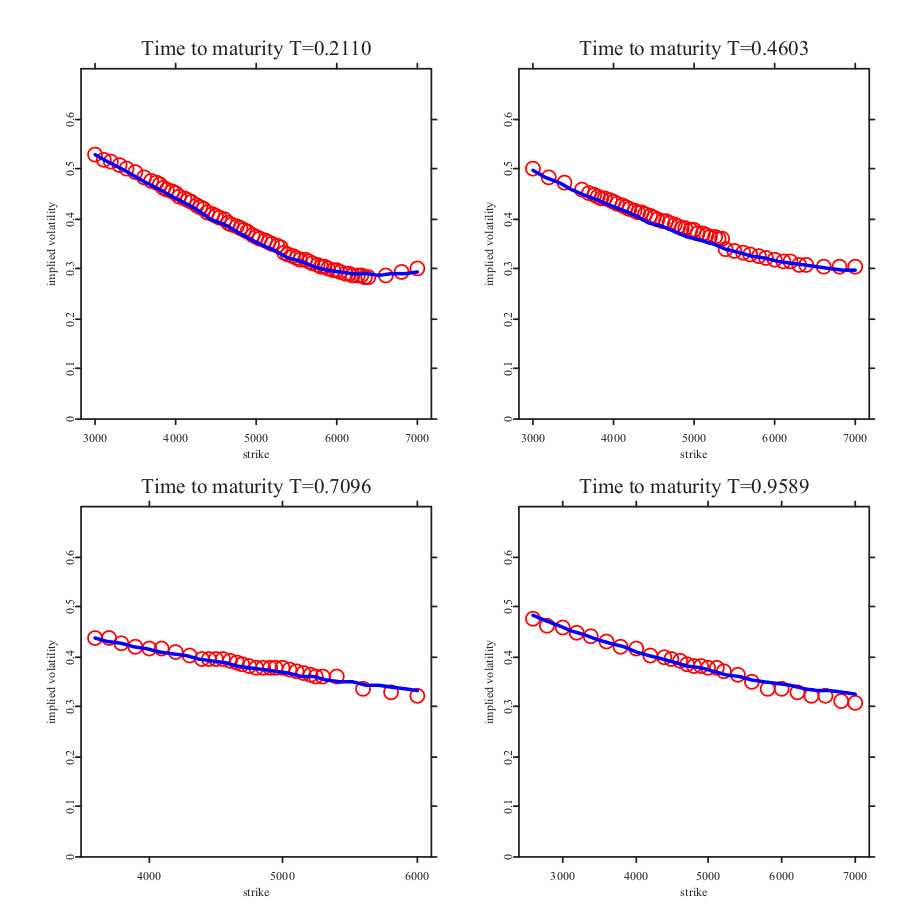
На графике в начале поста показана экстраполяция подразумеваемой волатильности опционов на индекс DAX, вычисленной по модели Бейтса для разных сроков до экспирации. Как вы можете заметить, даже на периодах, близких к экспирации, модель хорошо воспроизводит рыночные цены опционов ( выраженных через волатильность из формулы Блэка-Шоулза).
Это последняя модель, рассмотренная в цикле статей про улыбку волатильности. На моей практике она оказалось лучшей из множества применяемых мной моделей на российском рынке, поэтому рассмотрение остальных существующих аппроксимаций цен опционов не имеет особого смысла.














W = new double[32];
X = new double[32];
int info = 0;
alglib.gqgenerategausslegendre(32,out info, out X, out W);
32 — это количество узлов вычисления ( этой цифры достаточно для точности)
W — веса, X — узлы
надо что нибудь попроще… тут пересекается — покупаем, тут зашло за уровень 100 — продаем… а так думаю 99.9% на смартабе вас не поймут ))
и вообще не понимаю, почему с такими познаниями вы еще не в списке форбс ну или как минимум в какомнибудь крутом американском хедж фонде…?
а на что тогда надеятся нам смертным