Оптимальная доля счета для торговли
Чтобы лучше понять, насколько важна используемая доля счета, временно отойдем от опционов и рассмотрим игру, которую предложил Ральф Винс в своей книге «Математика управления капиталом». Ставим на кон какую-то долю от счета и с вероятностью 50% либо утраиваем поставленные деньги, либо их проигрываем. Матожидание у такой игры положительное, и очевидно, что тут можно хорошо заработать. Но вот какую долю от имеющихся денег ставить каждый раз на кон? Если делать слишком маленькую ставку, то выигрыш будет, но небольшой, и пользы будет мало. Если увеличивать долю поставленных денег, то счет будет расти все быстрее. Но, с другой стороны, если поставить слишком большую долю, например, каждый раз ставить всю имеющуюся сумму, то с вероятностью 50% она будет потеряна. Т.е. игра для нас окажется совсем
Решил перепроверить это и написал программку, которая моделирует заданное кол-во сделок для заданного F (используемая доля счета): 0.01, 0.02, ..., 0.99, 1.00. И для каждого такого F считает TWR (во сколько раз увеличился/уменьшился счет после всех сделок). Вот какой график получился:
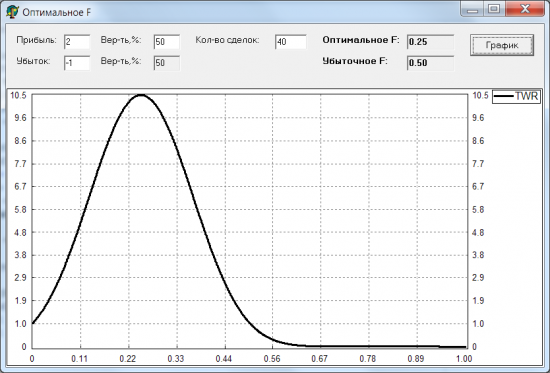
Действительно, оказалось, что максимум TWR достигается при F = 0.25 и равен 10.5 (весь счет увеличился в 10.5 раз). Интересно, что при F > 0.5 счет начинает не расти, а убывать (TWR < 1). Значит, если ставить каждый раз на кон более половины счета, то при достаточном кол-ве сделок счет неизбежно будет слит.
Но как можно вычислить оптимальное F, не прибегая к моделированию сделок? Введем новое понятие - функция полезности. Она будет показывать для каждого прироста счета, насколько это приращение было полезно для нас. Anon предложил использовать в качестве функции полезности натуральный логарифм (Ральф Винс в своей третьей книге тоже советует Ln, вот здесь его рассуждения на эту тему).
Имея функцию полезности, мы можем посчитать ее значения для каждого возможного исхода игры. А используя распределение вероятностей этих исходов, можем посчитать матожидание этой функции на заданном распределении, т.е. как бы среднюю полезность. И можем это сделать для каждого возможного значения F, от 0 до 1. Назовем новую функцию: МОП(F) (решил так назвать по первым буквам МатОжиданиеПолезности). Вот какой у нее получается график для рассматриваемой игры (нормировал и привел ее к масштабу графика TWR):
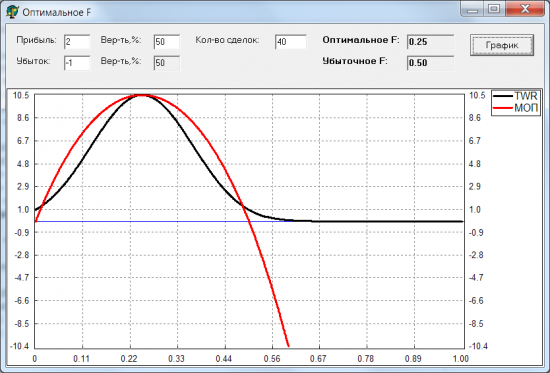
Видно, что максимум функции МОП совпадает с максимумом функции TWR. При F = 0 и 0.5 МОП равна нулю, т.е. при таких ставках мы не будем ни зарабатывать, ни терять деньги. При F > 0.5 матожидание полезности < 0, соответствует тому, что счет будет таять при таком F. Провел несколько экспериментов с исходными параметрами игры, и каждый раз максимум функции TWR совпадал с максимумом МОП. Т.е. теоретические расчеты совпадали с моделированием сделок. Вот несколько примеров:
- Выигрыш 2 к 1 с вероятностью 80%
- Выигрыш 3 к 1 с вероятностью 30%
- Выигрыш 1 к 1 с вероятностью 50%
- Выигрыш 1 к 1 с вероятностью 30%
Последние два графика показывают, что если матожидание исхода игры = 0 или отрицательное, то оптимальное F = 0. И любая ненулевая ставка неизбежно будет приводить к убытку.
Вернемся теперь к опционам. Применяя эту же технику, вычисляем МОП на распределении вероятностей и находим оптимальное F. Максимальное МОП, соответствующее этому F, примем за общую оценку позиции. Чем больше матожидание полезности у комбинации, тем лучше (полезнее) для нас эта комбинация. Вот пример, какие получились оценки для некоторого списка стандартных комбинаций:
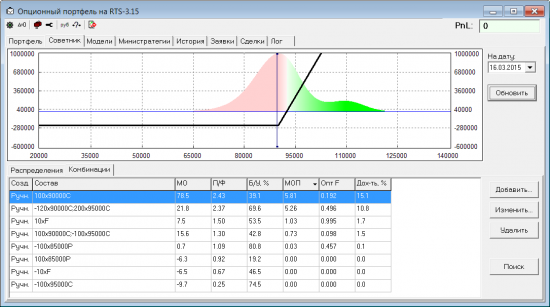
В отличии от прошлой оценки через свертку теперь не нужно ломать голову над весами для свертки. МОП сразу учитывает и доходность, и риск. Отношение к риску регулируется выбором функции полезности. Если берем Ln — у нас «неприятие риска». Если что-то вроде Sqr — «жажда риска» (чем больше ожидаемая доходность, тем все более и более полезной считаем комбинацию).
Лучшей комбинацией (из рассмотренных) в этот раз получился «лонг колл». Оптимальное F у него 0.192, т.е. если такой колл стоит 100, а у нас на счету 1000, то самым оптимальным будет купить 2 колла. Если же не послушаться математики и купить, например, 9 контрактов (F = 0.9), то ожидаемая доходность, конечно, вырастет (с 15% до 70%), но теперь с вероятностью почти 60% мы можем потерять 90% от счета. О чем нам и говорит новая оценка МОП этой позиции, которая стала хуже всех остальных:
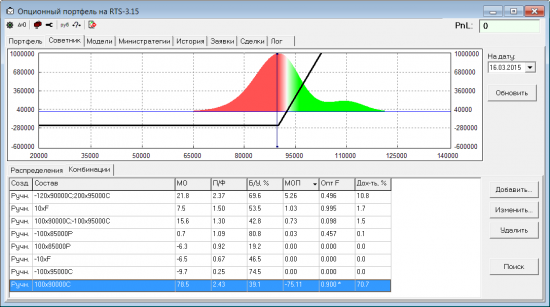
Это доказывает, что даже потенциально самую лучшую комбинацию можно превратить в очень не полезную для счета позицию, если открыть ее слишком большим объемом.
Подведем итог: если у нас есть распределение вероятностей (в которое верим), и есть функция полезности (которая отражает наши предпочтения к риску), то для любой комбинации можно точно вычислить ее оптимальный объем.
МО выигрыша равно нулю.
вероятность выигрыша 25% размер выигрыша 0,1 размер проигрыша -0,033, какое F она казать будет?
UPD ой, 25% это нулевая сумма, ну пусть будет 30%
Выигрыш 3 к 1 или 0,1 к 0,33 имеют одинаковые пропорции, но 3 это утроить депо а 0,1 — ясный пеппер, некислый, но вполне реальный доход со сделки внутри дня — 10% от депо. Вот только закавыка, чтобы сделать эти 0,1 мне нужно входить на 75процентов от депо, а не на восемь.
Что-то мутит ваш железный разум, тут две взаимозависимые величины — размер позиции и размер выигрыша, чем больше одно, тем больше другое.
Вот из верхних примеров 30на70 3 к 1, F=0,07. я смутно себе представляю как поседеют мои тестикулы пока я дождусь утроения счета за одну сделку, войдя позой размером 7 процентов от депо. Тут даже кухонное плечо не спасет :)))
Не совсем. Имхо, правильнее так: «чем больше размер позы, тем больше _потенциальный_ выигрыш, и тем больше потенциальный убыток.
Если вероятность убытка очень маленькая, то, да, программка советует увеличивать размер позы. Вот график для игры Выигрыш 1 к 1 с вероятностью 95%. При стремлении вероятности выигрыша к 100%, F -> 1.
Но если вероятность убытка достаточно большая, то F должен быть небольшим. Иначе потенциальный убыток может нанести слишком большой урон счету, и даже положительное матожидание не поможет его восстановить.
Гораздо реальнее промежуток от 0,01 до 0,2 хотя 20% это тоже огромная удача.
При этом вероятность убытка в отдельной сделке в реальной жизни около 50% — то есть она большая.
Я собственно и задал вопрос чисто из меркантильного интереса, может если есть идеальная пропорция задействованного капитала, мне стоит к ней стремиться? :)
исходя из того что считает программа получается довольно анекдотичный расклад:
1)чтобы заработать 10% в сделке, я должен задействовать больше половины капитала. (убыток если таковой случится будет около 1,5-3%)
2)реальное отношение количества убыточных сделок к выигрышным примерно 3 к 1 — это в среднем
3) реальное отношение профита к убытку в одной сделке колеблется от 2к1 до 7к1 редко-редко больше, и в среднем не считал, но думаю что немного больше чем 3к1 — то есть матожидание системы положительное но не так чтобы 95% что-то вроде 52-55 ИМХО
4) прога говорит что для того чтобы не слить в долгосроке я должен уменьшить задействованный капитал до 7% на сделку, но при этом как-то умудриться продолжать работать с той же доходностью 10% от депо в хорошей сделке.
Вопрос КАК? :))))
Но более правильная постановка задачи для этой программки, когда в случае проигрыша теряется вся ставка. Для такой постановки +300%/-100% (к ставке) 50%/50% — оптимальное F = 0.33.
Эта игра ведь была просто для иллюстрации проблемы с долей счета. В ней всего два исхода, и использовалось простейшее распределение вероятностей (кажется, оно называется распределение Бернулли). Сравнивать результаты этой программки с реальной торговлей, наверное, неправильно. Там ведь совсем другое распределение, более сложное.
Потеря всей ставки, ну для голых опционов, это нормально, так что имеет право быть.
Спасибо
Рынок может просто измениться, но это будет видно только посфактум. Будьте аккуранее.
Винс в игровой статистике с известным, и что важно! постоянным матожиданием это одно, реальный рынок — есть реальный рынок, все гараздо сложнее.
Гениально.
Варьируем p (probability)
Варьируем K (profit/loss)
Варьируем f от fKelly/3 до fKelly
N(количество сделок) 20,100,1000
Для каждых значений находим распределение вероятности максимальных просадок
Выяснится, что при использовании fKelly на дистанции 1000 сделок существует очень высокая вероятность (>80%) просадить 80% счета.
Также посмотрите, как сильно смещается кривая этого распределения, если Вы ошиблись в вероятности сделки на 5%. Тут есть точки крутого перегиба. Например, Вы решили, что совершаете сделку с вероятностью p и profit/loss=K. Выбрали максимальный f, например, исходя из предположения, что на дистанции 1000 сделок вы не хотите иметь просадку больше 35% с вероятностью больше 80%.
Если окажется, что на дистанции вы ошиблись и вероятность не p, а p-5%, то применение данного f может привести к тому, что с вероятностью 80% будет просадка более 35%.
Все это к тому, что копните глубже.
Применение fKelly имеет подводные камни. И его точно не стоит применять на весь депозит (если он у Вас последний :)).
И последнее. Данная модель построена на предположении независимости сделок, что на практике не так. Скорее у вас есть группы зависимых сделок. Группы между собой независимы.
Поизучайте, как применяли fKelly в блэкджеке. Там ситуация похожа: «холодная» и «горячая» колода — это зависимые события. Игры, разделенные перемешиванием колоды — независимые.