19 октября 2014, 16:33
Основы теории вероятностей или самоуверенным неучам посвящается
Пост по мотивам предыдущего: smart-lab.ru/blog/210413.php
Который в свою очередь являлся комментарием к: smart-lab.ru/blog/210372.php
Пост мотивирован комментариями (к моему предыдущему посту) самоуверенных неучей, которые демонстировали свое невежество чересчур агрессивно.
Причиной дискусси возникшей явлейтся тот факт, что при решении задач связанных с вероятностями люди слишко легкомысленно доверяются своей интуции. Всем известный парадокс Монти-Холла является ярким подтверждением этому. Одним из способов решения данной проблемы является моделирование задачи на компьютере. Поэтому тем, кто умеет программировать, настоятельно рекомендуется все свои решения задач связанных с вероятностями и статистикой проверять, используя данный метод.
Однако сегодня я всё же обойдусь без компьютера и продемонстрирую решение задачи из поста monte_carlo, фактически используя только ручку и листок бумаги.
Задача.
Задано:
1) начальная точка торговли: 0 пункт
2) тейк профит: 3 пункт
3) стоп лосс: -1 пункт
4) движение цены равновероятно
Найти: вероятность стоп лосса, вероятность тейк профита.
Вот НЕправильное решение monte_carlo из его поста:
«Теперь давайте посмотрим, какая будет вероятность при увеличении тейка в 3 раза по сравнению со стопом. Т.е. ТР = 3 тика, а стоп по-прежнему – 1 тик. По логике большинства, вероятность срабатывания стопа «чисто теоретически» и «при прочих равных условиях» (т.е. когда движение вверх и вниз – равновероятно) должна быть равна 2/3, а тейка 1/3. Давайте посмотрим так ли это.
Для этого выявим все возможные варианты (траектории) для 3 тиков:
Правильное ревешение:
Нарисуем следующий граф вероятностей
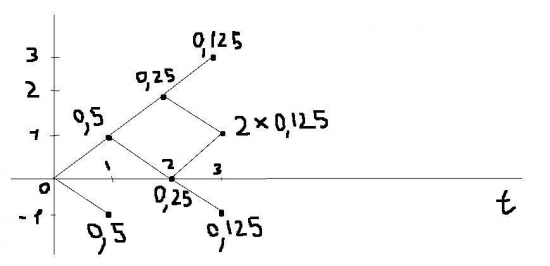
Пояснения:
Из нулевой начальной точки цена с одинаковой вероятностью (0,5) может пойти как в +1, так и в -1.
1 тик: в -1 один из путей для цены завершается. Однако в точке +1 движение продолжается.
2 тик: события, куда пойдёт цена из точки +1, снова равновероятны, но они пополам уже делят не единицу (как в нулевой точке), а 0,5. Поэтому их вероятности равны 0,25.
3 тик: можно только сделать пояснение, что поскольку в точку +1 ведут два пути, вероятность умножется на два.
Сумма вершин дерева должна быть равна единице.
Как это ни может показаться удивительным, но решение monte_carlo для трёх тиков численно равно данному результату.
Но уже далее становится понятно, что его решение неверно.
Дерево вероятностей для 4-х тиков:
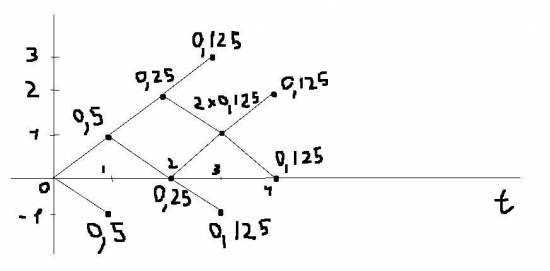
Всё аналогично.
Продолжая процесс, дерево получается следующим:
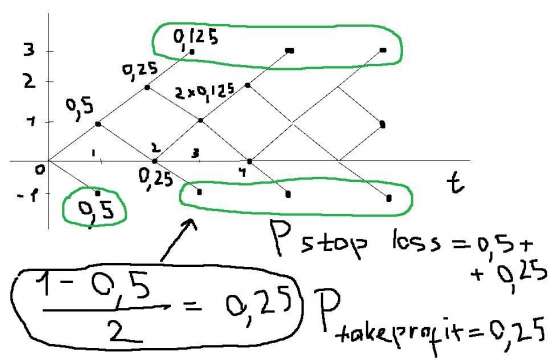
Из него собственно и находятся искомые вероятности.
Поскольку с увеличением времени вероятности в точках +1 и +2 стремятся к нулю (уже на десятом тике они достаточно небольшие), то ими можно пренебречь.
Тогда вероятности, обведенные зелёной линией (за исключением 0,5) должны быть равны. Отсюда и вычисляются вероятности тейк профита и стоп лосса.
Расчёты приведены на картинке. Вероятность стоп лосса = 0,75; вероятность тейк профита = 0,25; их отношение = 3:1.
Моделирование задачи на компьютере, о котором я упоминал в своем прошлом посту, подтверждает правильность полученных результатов.
Спасибо за внимание.
Который в свою очередь являлся комментарием к: smart-lab.ru/blog/210372.php
Пост мотивирован комментариями (к моему предыдущему посту) самоуверенных неучей, которые демонстировали свое невежество чересчур агрессивно.
Причиной дискусси возникшей явлейтся тот факт, что при решении задач связанных с вероятностями люди слишко легкомысленно доверяются своей интуции. Всем известный парадокс Монти-Холла является ярким подтверждением этому. Одним из способов решения данной проблемы является моделирование задачи на компьютере. Поэтому тем, кто умеет программировать, настоятельно рекомендуется все свои решения задач связанных с вероятностями и статистикой проверять, используя данный метод.
Однако сегодня я всё же обойдусь без компьютера и продемонстрирую решение задачи из поста monte_carlo, фактически используя только ручку и листок бумаги.
Задача.
Задано:
1) начальная точка торговли: 0 пункт
2) тейк профит: 3 пункт
3) стоп лосс: -1 пункт
4) движение цены равновероятно
Найти: вероятность стоп лосса, вероятность тейк профита.
Вот НЕправильное решение monte_carlo из его поста:
«Теперь давайте посмотрим, какая будет вероятность при увеличении тейка в 3 раза по сравнению со стопом. Т.е. ТР = 3 тика, а стоп по-прежнему – 1 тик. По логике большинства, вероятность срабатывания стопа «чисто теоретически» и «при прочих равных условиях» (т.е. когда движение вверх и вниз – равновероятно) должна быть равна 2/3, а тейка 1/3. Давайте посмотрим так ли это.
Для этого выявим все возможные варианты (траектории) для 3 тиков:
- Три тика вверх
- Два тика вверх, один тик вниз
- Один тик вверх, два тика вниз
- Один тик вверх, один тик вниз, один тик вверх
- Три тика вниз
- Два тика вниз, один тик вверх
- Один тик вниз, два тика вверх
- Один тик вниз, один тик вверх, один тик вниз
Правильное ревешение:
Нарисуем следующий граф вероятностей

Пояснения:
Из нулевой начальной точки цена с одинаковой вероятностью (0,5) может пойти как в +1, так и в -1.
1 тик: в -1 один из путей для цены завершается. Однако в точке +1 движение продолжается.
2 тик: события, куда пойдёт цена из точки +1, снова равновероятны, но они пополам уже делят не единицу (как в нулевой точке), а 0,5. Поэтому их вероятности равны 0,25.
3 тик: можно только сделать пояснение, что поскольку в точку +1 ведут два пути, вероятность умножется на два.
Сумма вершин дерева должна быть равна единице.
Как это ни может показаться удивительным, но решение monte_carlo для трёх тиков численно равно данному результату.
Но уже далее становится понятно, что его решение неверно.
Дерево вероятностей для 4-х тиков:

Всё аналогично.
Продолжая процесс, дерево получается следующим:

Из него собственно и находятся искомые вероятности.
Поскольку с увеличением времени вероятности в точках +1 и +2 стремятся к нулю (уже на десятом тике они достаточно небольшие), то ими можно пренебречь.
Тогда вероятности, обведенные зелёной линией (за исключением 0,5) должны быть равны. Отсюда и вычисляются вероятности тейк профита и стоп лосса.
Расчёты приведены на картинке. Вероятность стоп лосса = 0,75; вероятность тейк профита = 0,25; их отношение = 3:1.
Моделирование задачи на компьютере, о котором я упоминал в своем прошлом посту, подтверждает правильность полученных результатов.
Спасибо за внимание.
Читайте на SMART-LAB:

#MGKL: Купонные выплаты по облигациям за февраль — 100 млн руб.
В феврале ПАО «МГКЛ» в срок и в полном объёме исполнило обязательства перед держателями облигаций. Общий объём купонных выплат составил 100 527 500 рублей. 💼 Выплаты произведены по...
27.02.2026
Обновление кредитных рейтингов в ВДО и розничных облигациях (ООО «АСПЭК-Домстрой» подтвержден BB-.ru, ООО «ПЗ «Пушкинское» понижен D|ru|, ООО «ЦЕНТР-РЕЗЕРВ» понижен С(RU))
🟢ООО «ФЭС-Агро»
Эксперт РА подтвердил рейтинг кредитоспособности на уровне ruBBB-, прогноз по рейтингу стабильный. ООО «ФЭС-Агро» входит в тройку крупнейших дистрибьюторов семян, средств...
09:15











будет к вам просьба предложите свою математику в моём посте по обозначенной в этом посте проблеме.
заранее Вам благодарен
А вероятность нужно считать на рынке, а не на бумаге.