Measuring Historical Volatility

Вычисление подразумеваемой (implied) волатильности – задача хоть и не тривиальная (требуется знание численных методов), но весьма простая. К тому же  мы всегда имеем уникальное единственное решение – значение волатильности для заданного опциона. С исторической (historical) волатильноcтью дела обстоят несколько сложнее. Количество наблюдений, участвующих в расчетах, и метод ee оценки оказывают сильное влияние на конечный результат.

За основу данного поста взят материал из моей статьи в Financial One.

Рассмотрим основные методы оценки исторической волатильности и разберем их особенности.

В срочной секции Московской Биржи активно торгуются фьючерсы на обменный курс доллара США к рублю и опционы на этот контракт. В последнее время волатильность данного фьючерсного контракта возросла. Оценим его историческую волатильность.

Так как срочный контракт имеет ограниченный срок обращения, заменим его спотовым активом – валютной парой USD/RUB. Корреляция этих активов крайне высока. Для учета разницы во времени торгов будем использовать внутридневные цены только из временного интервала, соответствующего дневной торговой сессии на срочном рынке Московской биржи – с 10:00 до 18:45. Для этих данных вычислим дневные цены: open (O), high (H), low (L), close (C ) – и будем использовать полученные данные для расчета исторической волатильности.

Оценку волатильности будем производить по 22 торговым дням (примерно 1 месяц) следующими методами: Close-to-close, Parkinson, Garman-Klass, Rogers-Satchell, Garman-KlassYang-Zhang extension, Yang-Zhang.

1. Close-to-close (C )

Наиболее часто употребляемый метод для оценки исторической волатильности. В расчетах используются только цены закрытия (close). Формулы и подробное описание смотрите на моем сайте quant-lab.com

2. Parkinson (HL)

При оценке данным методом используются максимальные (high) и минимальные (low) цены торговой сессии. Данный метод не учитывает jumps (прыжки – разрыв в ценах закрытия и открытия между сессиями). Также метод не учитывает drift (направленное движение, тренд). В среднем это метод недооценивает волатильность, но тем не менее он эффективней предыдущего метода (см. Таблицу 1).

3. Garman-Klass (OHLC)

Оценка наиболее эффективна для активов с динамикой броуновского движения, с нулевым дрифтом и без прыжков. Хотя данный метод эффективнее двух предыдущих, тем не менее, он как правило недооценивает уровень волатильности.

4. Rogers-Satchell (OHLC)

Эффективность данного метода соизмерима с методом Garman-Klass. Однако это метод учитывает дрифт, но недостаточно хорошо «справляется» с прыжками, что приводит к недооценке волатильности.

5. Garman-Klass Yang-Zhang extension (OHLC)

Этот метод позволяет учитывать разрывы в ценах между открытием торговой сессии и закрытием предыдущей (jumps), но подразумевает нулевой дрифт.

6. Yang-Zhang (OHLC)

Наиболее мощный метод для оценки исторической волатильности, имеющий минимальный уровень ошибки. Оценка равна взвешенному среднему оценки Rogers-Satchell, close-open волатильности и open-close волатильности.

Результаты сравнения методов по признакам: какие данные используются, учитываются ли drift и jumps, а также эффективность каждого метода согласно [1] приводятся в Таблице 1.

Таблица 1. Сравнение методов


Динамика обменного курса USD/RUB и значения волатильности, рассчитанные указанными выше методами изображены на Рисунке 1. Период: 2013-01-08 – 2014-06-13.

Рисунок 1. Динамика обменного курса USDRUB и исторические волатильности


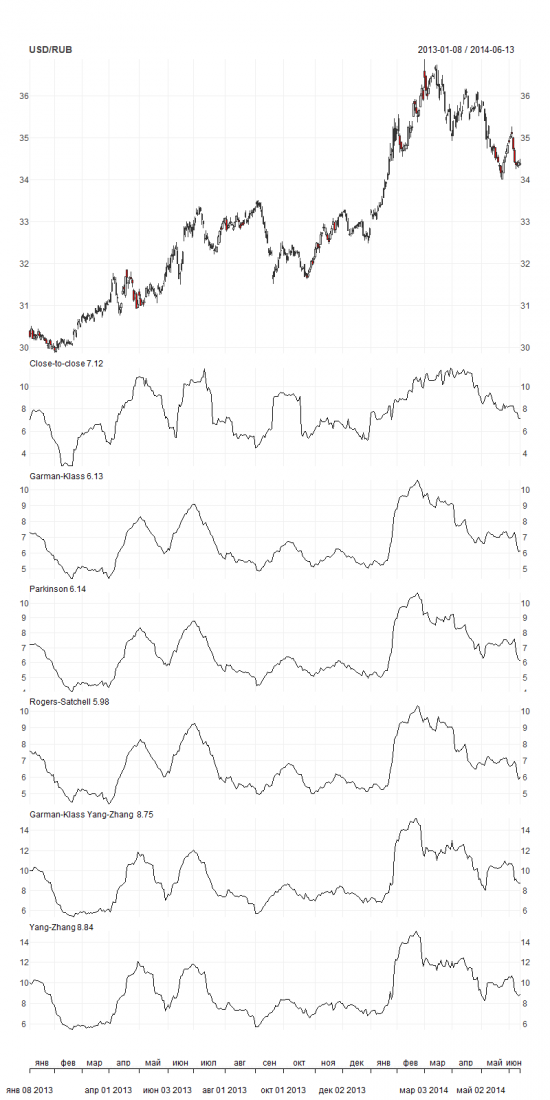
Максимальное текущее значение волатильности показывает метод Yang-Zhang, имеющий максимальный рейтинг согласно Таблице 1. Стоит отметить, что это не случайно, т.к. остальные методы склонны занижать оценку волатильности.

Интересно, что динамика волатильности на двух нижних графиках не согласуется с динамикой на остальных графиках, на которых волатильность обновила локальный минимум. Вероятная причина этого – наличие прыжков, наблюдаемых в последнее время на рынке. Принимая это во внимание, а также тот факт, что подразумеваемая волатильность сейчас находится на своих локальных минимумах, можно сделать предположение, что рынок недооценивает волатильность USD/RUB.

На Рисунках 2 – 7 представлена динамика исторической волатильности, рассчитанной различными методами, в сравнении с ее средними значениями за месяц, квартал, полгода и год.

Рисунок 2. Историческая волатильность Close-to-Close


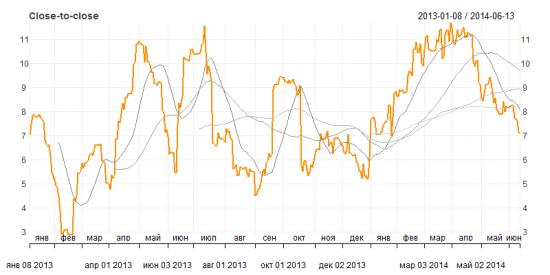
Рисунок 3. Историческая волатильность Garman-Klass


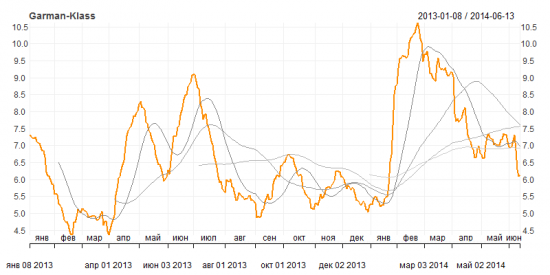
Рисунок 4. Историческая волатильность Parkinson


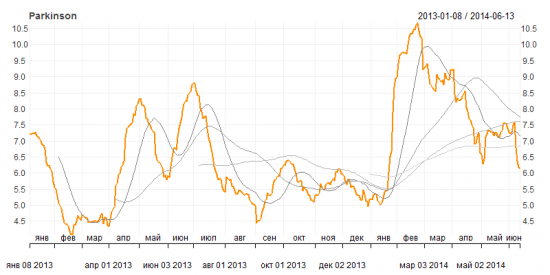
Рисунок 5. Историческая волатильность Rogers-Satchell


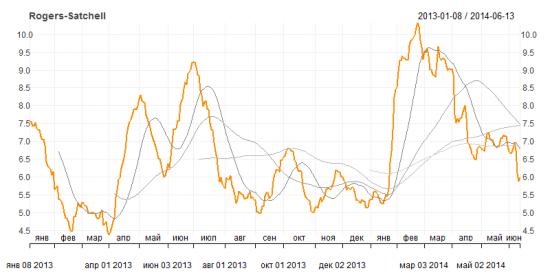
Рисунок 6. Историческая волатильность Garman-Klass Yang-Zhang extension


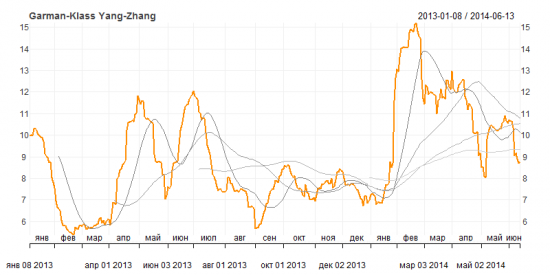
Рисунок 7. Историческая волатильность Yang-Zhang


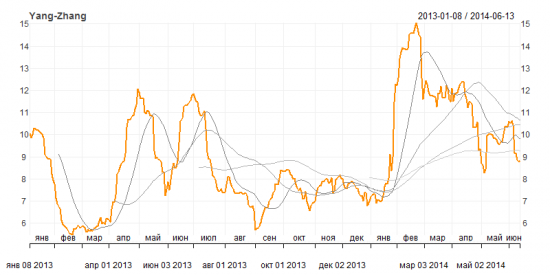
Согласно этим графикам волатильность снижается и находится сейчас ниже своего среднего годового значения, имеющего нейтральную динамику последние два месяца. Среднемесячная волатильность тем не менее находится выше среднего значения волатильности за год, но ниже квартального и полугодового. Тот факт, что волатильность, не встречая сопротивления, снизилась ниже своих полугодовых и годовых средних значений, придает уверенности, что нисходящий тренд в динамике волатильности достаточно сильный, и это движение вероятно продолжится.