Недоинвестированные купоны
Вновь взяться за перо меня побудили пост Андрея Х. о доходности к погашению (YTM) и чудовищные проявления ригоризма в комментариях к нему.
Вот утверждения автора, которые подверглись жестокой обструкции:
YTM (Yield to Maturity) — общий доход, ожидаемый от облигации, если облигация удерживается до погашения.
Этот вид доходности предполагает реинвестирование купонов внутри года и позволяет наиболее корректно сравнивать бумаги с разными параметрами (срок, купон, изменение цены)
И в самом деле, YTM это не “общий доход”, а ставка дисконтирования. Мы ведь помним, чем качественно отличаются доход, прибыль и процентная ставка? А выражение “реинвестирование купонов внутри года” правильно будет заменить на “сложную ставку процента ”
Конечно, Андрей Х. создает такие миниатюрные посты не в просветительских целях, а чтобы в очередной раз прорекламировать свои соцсети и телеграм-канал. Завсегдатаи смартлаба это понимают, и не имеют привычки придираться к содержанию и осуждать автора за мелкие недочеты. Мало кто ожидал, что в комментариях возникнет агрессивный неофит, гневно размахивающий старой публикацией малоизвестных американских финансистов.
Аннотация к этой заметке напоминает читателю о “распространенном заблуждении, которое встречается в посвященных инвестициям текстах и популярной литературе, а именно, что для получения доходности к погашению по купонной облигации инвестор должен реинвестировать купонные платежи” (выделение шрифта — моё) В вводной части тезис усиливается: “Ошибочное утверждение заключается в том, что держатели облигаций должны реинвестировать купоны, чтобы “заработать” рассчитанную доходность к погашению.” (оно как раз не ошибочное, а очень даже верное, но мы забегаем вперед)
Далее авторы приводят отдельные неаккуратные фразы представителей академической литературы. Например, такую: “доходность к погашению предполагает, что все процентные платежи реинвестируются по ставке, эквивалентной доходности к погашению" В данном контексте “предполагает” может быть легко интерпретировано как “обязательно учитывает в формуле расчета”, что, конечно, ошибочно.
В следующем разделе — “Yield-to-Maturity is the Return Earned” — авторы обращают внимание, что о реинвестировании не говорится и в хорошо известном определении “доходности к погашению”. Это ставка дисконтирования, при которой приведенная стоимость денежного потока по облигации равна ее цене. Кроме того, они наглядно показывают, что в самом принципе расчета доходности нет никакого реинвестирования купонов. В разделах “The Coupon Reinvestment Assumptions Persistence” и “Conclusion” авторы излагают очевидные вещи; по сути, это именно то, что я пытался разъяснить в комментариях к посту Андрея Х. В целом, явных терминологических ошибок текст не содержит. Его пафос направлен против контаминации устойчивых понятий. В этом смысле он, безусловно, полезен, и все же представляет собой не революционное отрицание вековых заблуждений, а никому не нужную борьбу с ветряными мельницами.
──────────────── • ✤ • ─────────────────
Как обычно, корни противоречий лежат в плоскости семантики. В нашем случае необходимо разделить понятия заработать доходность и рассчитать доходность.
Принцип расчета доходности к погашению действительно не требует предположения о реинвестировании купонов. Правда, и не запрещает его прямо: можно формально реинвестировать купоны, затем использовать обычную методику дисконтирования и получить ту же самую доходность.
Однако, чтобы в момент погашения облигации заработать изначально рассчитанную доходность r, т.е. в реальности получить будущую стоимость, равную FV = PV⋅(1+r)ᵀ, необходимо реинвестировать купоны под эту же ставку r. Реинвестирование означает, что полученные купоны расходуются на приобретение доли в той же самой облигации.
Но обо всем по порядку.
──────────────── • ✤ • ─────────────────
Базовой концепцией в корпоративных финансах является временная стоимость денег (time value of money) Для начала нужно нарисовать линию времени (timeline) и расположить на ней части исследуемого денежного потока (денежный поток, stream of cash flows — серия платежей, соответствующих моментам времени сейчас и/или в будущем):

Предполагается, что наблюдатель находится на временной линии в момент t = 0, который соответствует текущей дате. Платежи могут быть как положительными (притоки денежных средств), так и отрицательными (оттоки).
Стоимость каждого платежа зависит от 1) времени его поступления и 2) даты оценки, которая не обязательно совпадает с t = 0. Для того, чтобы корректно сравнивать (или складывать) стоимости элементов денежного потока, необходимо все их “переместить” в одну и ту же дату оценки согласно определенному правилу.
Будущая стоимость (FV, future value)
Допустим, сегодня у нас на руках есть 1000 руб. и мы хотим найти эквивалент стоимости этой суммы через год. Если рыночная ставка процента составляет 20% годовых, мы можем использовать ее как обменный курс для продвижения по временной линии:
1000 руб. (сегодня) × 1.2 (рубль через год)/(рубль сегодня) = 1200 руб. (через год)
Для того чтобы узнать будущую стоимость 1000 руб. через два года (при условии неизменности рыночной ставки), мы повторяем процедуру :
1200 руб. (через год)×1.2 (рубль через два года год)/(рубль через год) = 1440 руб. (через два года)
Описанный процесс перемещения стоимости вперед во времени известен как компаундинг или сложное начисление процентов. В общем случае, для постоянной ставки r будущая стоимость (через n периодов) текущей выплаты величиной C может быть вычислена по формуле
FVₙ = C⋅(1+r)ⁿ
Рассчитанные на одну и ту же дату в будущем стоимости отдельных платежей необходимо складывать, чтобы получить будущую стоимость денежного потока в целом:
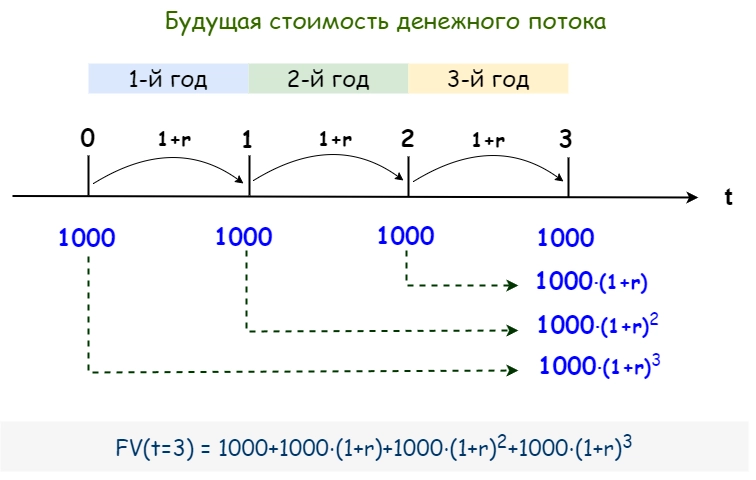
Приведенная стоимость (PV, present value)
Зеркальное правило действует для “переноса” стоимости денежных выплат в прошлое. Например, текущая стоимость ожидаемой через год суммы в 1000 руб. (при той же ставке 20% годовых) обменивается по “обратному” курсу:
1000 руб. (через год) ÷ 1.2 (рубль через год)/(рубль сегодня) = 833.33 руб. (сегодня)
Другими словами, чтобы “сдвинуть” стоимость ожидаемого платежа на год назад, мы умножаем ее на дисконт-фактор 1/(1+r), где r — действующая ставка процента. Этот процесс называется дисконтированием и его необходимо повторять для каждого периода. Если ставка r остается неизменной, текущая стоимость выплаты в размере C, ожидаемой через n периодов, может быть вычислена по формуле
PVₙ = C/(1+r)ⁿ
Стоимости отдельных платежей, рассчитанные на одну и ту же дату перед их поступлением, нужно складывать, чтобы получить приведенную стоимость всего денежного потока:

Накопленная стоимость
Изложенные выше правила (компаундинг и дисконтирование) хорошо знакомы даже начинающим инвесторам, их легко обнаружить на любом финансовом ресурсе. Куда менее известен тот факт, что эти правила можно комбинировать, чтобы получать накопленную стоимость на любую промежуточную дату между выплатами:
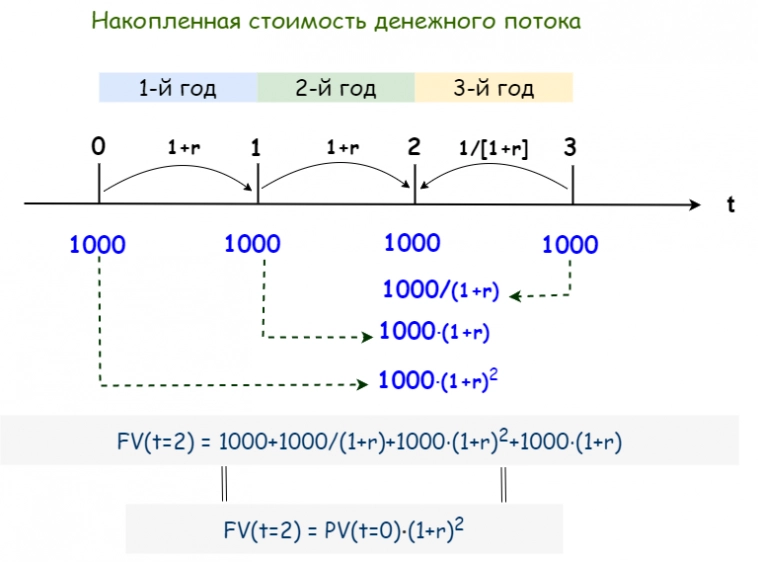
Более того, между приведенной и будущей (накопленной) стоимостью денежного потока с положительными выплатами существует глубокая взаимосвязь, если процентная ставка r остается постоянной для всех периодов начисления:
FV(k) = PV(0)⋅(1+r)ᵏ
Эта формула проверяется непосредственным математическим расчетом. Таким образом, чтобы найти накопленную стоимость в предположении неизменности процентной ставки, достаточно один раз рассчитать приведенную стоимость ряда платежей, а затем просто капитализировать ее к планируемой дате.
──────────────── • ✤ • ─────────────────
Как мы заметили выше, доходность к погашению — это ставка дисконтирования, для которой приведенная стоимость выплат по облигации равна ее цене. Поскольку эта стоимость всегда рассчитывается на дату t = 0, никакого реинвестирования в формуле не предусмотрено — ведь до получения денег их невозможно куда-либо вложить. Впрочем, если захотеть, то реинвестирование можно сделать искусственно, “переместив” купоны в будущее.
Рассмотрим пример двухлетней облигации с купонной доходностью 20%, торгующейся за номинал (в момент времени t = 0 происходит отток денежных средств в размере 1000 руб) Классическое дисконтирование денежного потока даст в этом случае доходность к погашению, равную ставке купона: YTM = 20%. Давайте изменим подход и “реинвестируем” купон 1-го года, чтобы найти его будущую стоимость. У нас возникнет виртуальная выплата в конце 2-го года, увеличенная на 20%. Если теперь провести новое дисконтирование, мы получим ту же самую доходность YTM — 20%:

Мы видим, что ничего страшного не случилось и доходность к погашению была правильно рассчитана в предположении реинвестирования купонов. Понятно, что в подобном “движении” стоимости купона по оси времени никакого практического смысла нет. Цель этого рассуждения лишь в том, чтобы показать: реинвестирование и доходность к погашению друг друга вовсе не исключают. Поэтому, того, кто хорошо освоил концепцию временной стоимости денег, не смутит небрежность формулировок. Когда академические издания упоминают про реинвестирование купонов, они на самом деле (довольно неряшливо) пытаются подчеркнуть различия между YTM и простой доходностью (simple yield). Простая доходность не подразумевает сложного исчисления процентов: номинальные значения всех будущих поступлений суммируются, результат сопоставляется с начальным вложением и затем приводится к годовым величинам (т.е. аннуализируется)
Еще одной причиной неистребимости фразы о реинвестировании купонов в различных трактовках YTM служит необходимость различать понятия доходность к погашению и доходность за период владения (horizon rate of return, holding period return, HPR) HPR представляет собой реализованную доходность на некотором горизонте, необязательно совпадающим с датой погашения облигации. Например, инвестор может держать пакет идентичных облигаций какое-то время, все полученные за это время купоны вкладывать в них же, а затем продать весь портфель, зафиксировав HPR.
Для расчета HPR самофинансируемого портфеля условие реинвестирования полученных купонов является обязательным, потому что данная процедура требует нахождения накопленной (будущей) стоимости облигации.
Если рыночные ставки изменяются со временем, HPR не будет совпадать с YTM даже в том случае, если удерживать облигацию до погашения. На представленной ниже анимации представлены выборочные траектории YTM, накопленной стоимости и HPR удерживаемой до погашения купонной облигации, если динамика процентных ставок подчиняется стохастическому процессу Орнштейна-Уленбека с возвратом к долгосрочному среднему. Использовано непрерывное начисление процентов и выплаты купона. Траектории HPR в начальной части графика не отображены, так как для небольших значений t разброс показателей доходности будет слишком велик, и это не позволяет четко разглядеть картину вблизи даты погашения.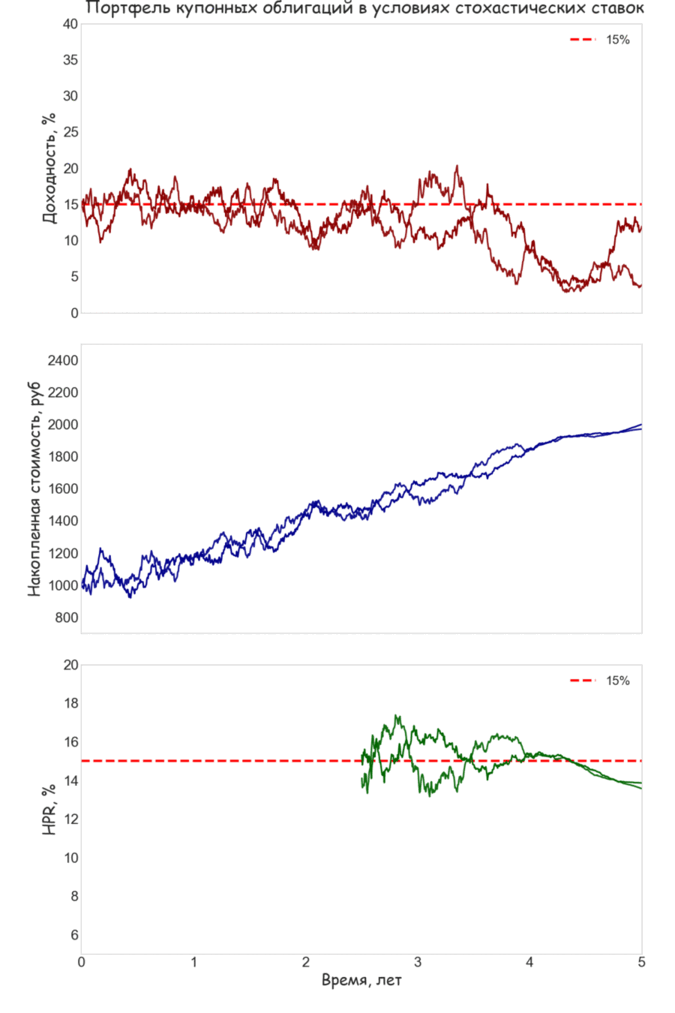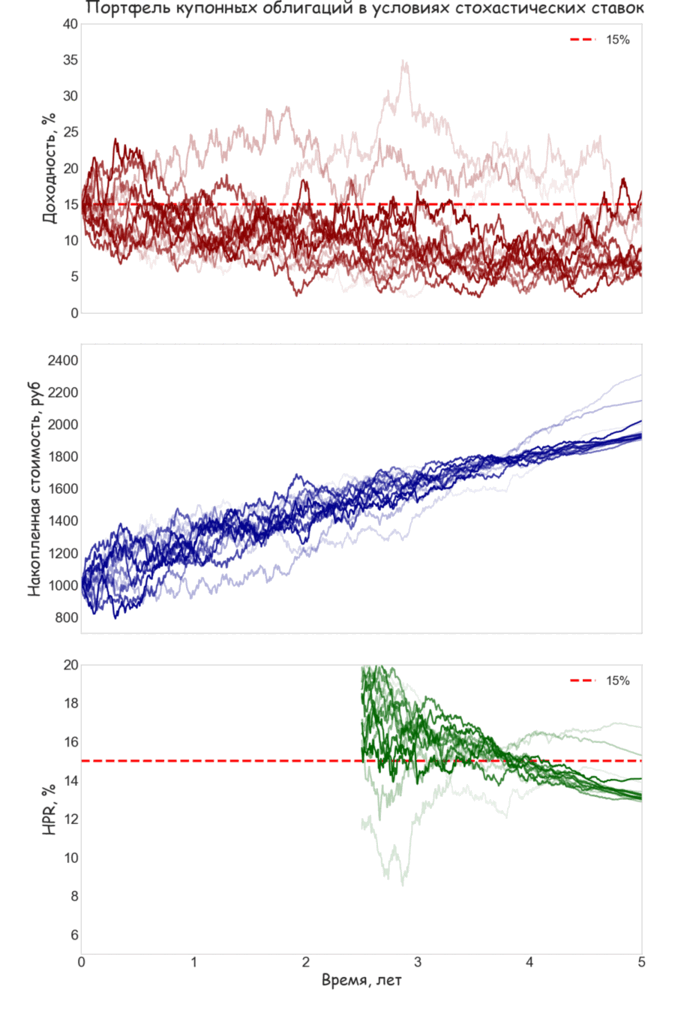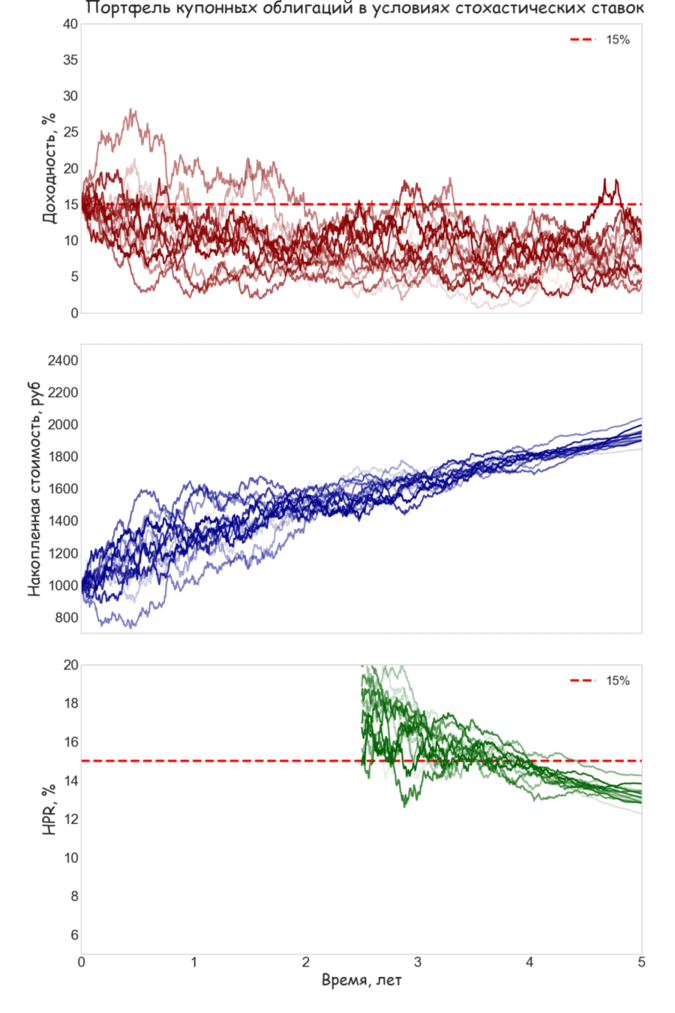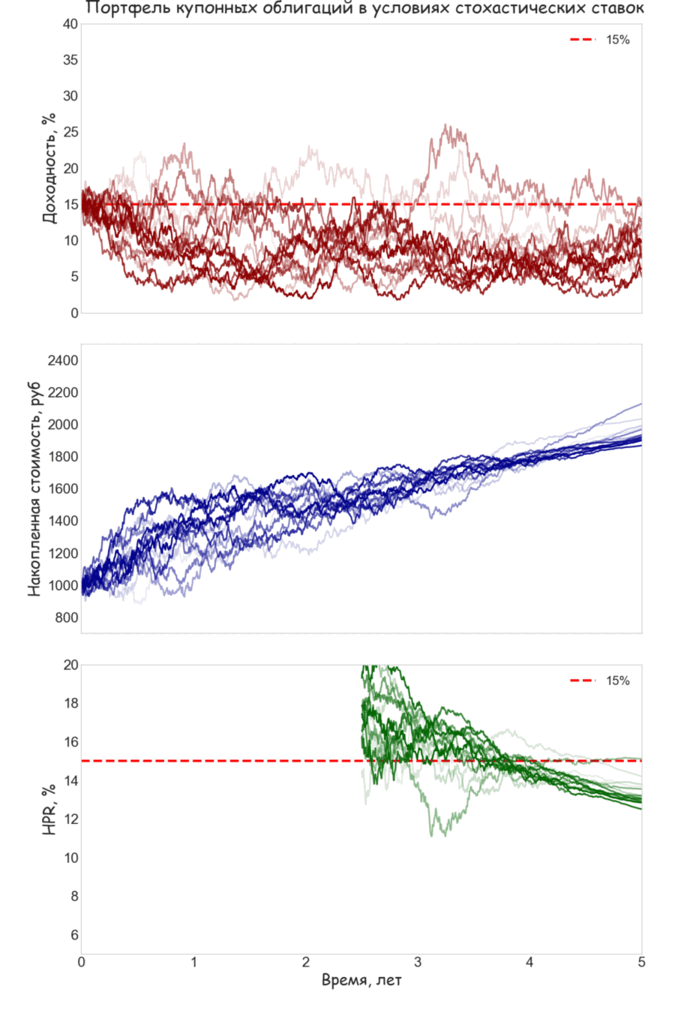
Мы специально предположили, что долгосрочное среднее (10%) находится ниже начальной YTM (15%) В результате выборочные траектории YTM имеют тенденцию к снижению. Это приводит к тому, что реинвестирование купонов происходит, как правило, под ставку меньшую, чем начальная YTM. Хорошо заметно, что HPR на дату погашения будет в таких случаях ниже 15%. Также можно обратить внимание, что вблизи точки дюрации (3.52 года) HPR часто имеет значение близкое к YTM, что объясняется действием частичной иммунизации.
Таким образом, авторы “некорректных” утверждений о доходности к погашению хотят сказать простую вещь: если инвестор смотрит на YTM облигации, он должен помнить, что не обязательно заработает будущий доход исходя из этой ставки. Так произойдет только если все до единого купоны будут реинвестированы под ставку YTM.
Дополнительные материалы о доходности и оценке простых облигаций можно прочесть в моих статьях:













Куплена облигации по номинала и купоном 20% раз в год. Купон постоянный.
Через год инвестор получает свои 200р купонного дохода,
идет реинвестировать в ту же облигацию и тут видит, что Сахипзадовна устроила очередной рывок в борьбе с инфляцией и теперь его облигация стоит не 1000р, а 200р.
Инвестор покупает и через год получает ещё 200р купонного дохода по старой 20% и 200р по новой, что дает ему 20% по старой и 100% по новой+500% в перспективе погашения через 39 лет. Но ситуация опять поменялась-Сахипзадовну отправили писать мемуары и ВВП сказал что теперь мы будем развивать кредитование и КС поэтому 3%. Облигации 1 и 2 взлетают до небес, но есть нюанс-теперь, на третьем году, облига стоит уже 1150р. И грустный инвестор покупает ее на все купоны… Мораль и вопрос- ну и как вообще рассчитывать адекватно в таких условиях «доходность к погашению»?