не увидел то что искал а искал выпуклость
Выпуклость
Выпуклость (Convexity) – свойство цен на облигации меняться ассиметрично, относительно изменения доходности. В типичном случае цена облигации возрастет больше при заданном сокращении доходности, чем уменьшение при таком же росте доходности [2 стр. 969].
Выпуклость (Convexity) – мера изменения Модифицированной Дюрации при изменении процентной ставки [8].
____________________________________________
Стоимость облигации, как функция, «дисконтирующая» платежи по ней в будущем и риски связанные с исполнением эмитентом облигации этих обязательств, определяется стоимостью денег во времени и премией за риск, обусловленный кредитным качеством эмитента.
Таким образом, колебания стоимости облигаций по своей природе имеют две основные причины: колебания рыночной процентной ставки и изменение кредитного качества эмитента, определяющего риск потери денег по данному вложению.
Процентный риск возникает в результате неблагоприятного движения (изменения) процентных ставок [7]. Этот вид риска может служить источником сверхприбыли. Однако принятие высокого уровня этого вида риска может сильно влиять на эффективность инвестиций в инструменты с фиксированной доходностью.
Ситуация не является столь очевидной, если речь идет об инвестициях в «долги» на срок, равный сроку оставшемуся до их полного погашения. А именно, если процентные ставки до момента выплаты возрастают, то можно лишь говорить об упущенной выгоде (недополученном проценте). С другой стороны, если «покупка» будущего платежа при фиксированной, оговоренной сегодня ставке осуществляется за счет займа под плавающий (пересматриваемый) процент, то рост такового может привести к отрицательным финансовым результатам (убыткам). Напротив, снижение уровня процентной ставки, позволит в данном случае «сэкономить» на обслуживании займа, и как следствие – получить более высокую прибыль.
Более того, процентная ставка влияет на приведенную к определенному моменту стоимость будущей выплаты. Таким образом, результат купли-продажи долга по теоретической стоимости до момента его погашения складывается из, собственно самого процента за период держания, и из прироста его приведенной стоимости в результате колебания процентной ставки.
Рассмотрим следующую ситуацию: ставка процента (стоимость денег за единицу времени) r на данный момент времени определена однозначно и не зависит от срока заимствования. По истечению времени t будет осуществлена выплата в размере F. При этом полностью отсутствует риски неплатежа, как по срокам, так и по объему.
При сделанных допущениях, текущая стоимость F, в рамках концепции временной стоимость денег, будет определяться по {bd.1}.

В отношение {1.1} справедливы следующие утверждения*(1):
Таким образом, если рассматривать текущую стоимость, как функцию процентной ставки, то приращению аргумента будет соответствовать приращение текущей стоимости, согласно {bd.2}. То есть приращение текущей стоимости со знаком «минус» прямо пропорционально произведению, собственно самой стоимости, времени до выплаты и коэффициенту дисконтирования для «единичного» интервала времени.

Классическую облигацию – облигацию с постоянным купоном – можно рассматривать как портфель, состоящий из дисконтных облигаций: каждый купон – дисконтная облигация, номиналом, равным ставке купона, и отдельно сумма основного долга. Формально, текущая стоимость потока платежей по классической облигации описывается формулой {bd.3}.
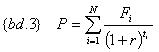
Зависимость приращения текущей стоимости рассматриваемого потока платежей от приращения процентной ставки определяется по {bd.4}.

Введем следующее обозначение – обозначение доли приведенной стоимости i-го платежа в текущей стоимости потока платежей:
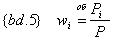
При этом заметим, что:
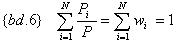
Тогда {1.4} перепишем в более удобном виде:
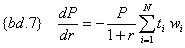
То есть, как и в случае с дисконтной облигацией — {bd.2}, приращение текущей стоимости потока платежей (что соответствует классической облигации или портфелю дисконтных и(или) классических облигаций) со знаком «минус» прямо пропорционально произведению, собственно самой текущей стоимости (приведенной стоимости портфеля), коэффициенту дисконтирования для «единичного» интервала времени, и средневзвешенному сроку платежей.
Дюрацией Маколея, или просто: Дюрацией (Macaulay duration, разработана и предложена Фредериком Маколеем в 1938) – называется средневзвешенный срок платежей по облигации – обозначение {bd.8} – исторически, одна из первых мер процентного риска облигаций.
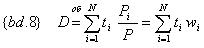
Отметим ряд свойств Дюрации Маколея:
Имея рассчитанную Дюрацию Маколея можно вычислить модифицированную Дюрацию:
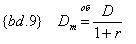
Таким образом, с помощью модифицированной Дюрации можно оценить колебания цены облигации при малых изменениях процентной ставки. На практике, для оценки колебаний текущей стоимости облигации (портфеля облигаций), при предполагаемом изменении процентной ставки применяют следующее приближение:
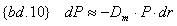
Выпуклость (Convexity) – свойство цен на облигации меняться ассиметрично, относительно изменения доходности. В типичном случае цена облигации возрастет больше при заданном сокращении доходности, чем уменьшение при таком же росте доходности [2 стр. 969].
Выпуклость (Convexity) – мера изменения Модифицированной Дюрации при изменении процентной ставки [8].
С математической точки зрения выпуклость является отношением второй производной текущей стоимости потока платежей к его стоимости: Рассчитать этот показатель можно, согласно {bd.11}, по формуле {bd.12}.

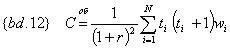
На практике для получения более точной оценки изменения текущей стоимости потока (цены облигации, или портфеля облигаций), по сравнению с {bd.10}, используют {bd.13}:
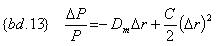
Таким образом, выпуклость позволяет более точно рассчитать изменение цены при малых изменениях требуемой доходности. Хороший обзор теории Дюрации и выпуклости можно найти в [1].
Пример: Облигация казначейства США с датой погашения 15 июня 2017 года и полугодовым купоном 8.875% годовых, текущей стоимостью, приблизительно 128.1231%, доходностью к погашению, в соответствии с принципами SIA*(2) — 5.228% годовых. Дата оценки 15 июня 2007 года.
Ближайший купон будет выплачен 15 декабря 2007 года, то есть о его выплаты осталось ровно одно «полугодие» — один период для начисления сложного процента. Текущая стоимость ближайшего купона:
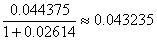
Доля текущей стоимости ближайшего купона в текущей стоимости облигации составляет 0.033479. Взвешенный срок платежа по нему также равен 0.033479 полугодия.
Следующий купон (второй по счету, начиная с даты оценки): срок до выплаты 2 полугодия. Его текущая стоимость:

Доля данного купона в текущей стоимости облигации 0.032889. Взвешенный срок платежа по данному купону 0.032889*2=0.065778.
И так далее …
Последний купон и основной долг: срок до выплаты 20 полугодий. Текущие стоимости:
Купон:
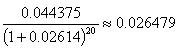
Основной долг:

До платежа последнего купона и основной суммы 0.02067 и 0.4659, соответственно. И взвешенные сроки выплат: 20*0.02067=0.413393 по купону, и 20*0.4659=9.317995 по основному долгу.
Теперь, просуммировав взвешенные сроки всех платежей, получим средневзвешенный срок платежа по облигации, то есть значение Дюрации Маколея – 14.46982 полугодий, или 7.234911 лет.
______________________________________________________
*(1) в [2 стр. 456] со ссылкой на [3] данные утверждения приводятся как «теоремы, связанные с оценкой облигаций.
*(2) SIA (Securities Industry Association) Semi-Annual Yield Conventions [6].
Литература:
1.Ливингстон Г. Дуглас. Анализ рисков операций с облигациями на рынке ценных бумаг. М: Информационно-издательский дом «Филинъ», 1998.
2.Шарп У., Александер Г., Бэйли Дж. Инвестиции: Пер. с англ. – М: ИНФРА-М, 2001. – XII, 1028 с.
3.Burton J. Makliel, “Expectation, Bond prices, and the Term Structure of Interest Rates”, Quarterly of Economics, 76, no 2 (may 1962), pp. 197-218.
4.Bertocchi M., Giancometti R., Zenios S. Risk factor analysis and portfolio immunization in the corporate bond market. 2000, November 2.
5.Fabozzi, Frank J., and T. Dessa Fabozzi, eds. The Handbook of Fixed-Income Securities. Burr Ridge, IL: Irwin. 4th ed., 1995, ISBN 0-7863-0001-9.
6. Mayle, Jan. Standard Securities Calculation Methods. New York: Securities Industry Association, Inc. Vol. 1, 3rd ed., 1993, ISBN 1-882936-01-9. Vol. 2, 1994.
7.Principles for the Management and Supervision of Interest Rate Risk. Basel Committee on banking Supervision. 2001. January. Материалы сайта http://www.bis.org/
Документация к ПО:
8.MATLAB: Financial toolbox documentation — Pricing and Computing Yields for Fixed-Income Securities// Mathworks Software http://www.mathworks.com/
Интернет ресурсы:
9.Bonds Screener //Материалы сайта http://www.finance.yahoo.com/
Выпуклость (Convexity) – мера изменения Модифицированной Дюрации при изменении процентной ставки [8].
____________________________________________
Стоимость облигации, как функция, «дисконтирующая» платежи по ней в будущем и риски связанные с исполнением эмитентом облигации этих обязательств, определяется стоимостью денег во времени и премией за риск, обусловленный кредитным качеством эмитента.
Таким образом, колебания стоимости облигаций по своей природе имеют две основные причины: колебания рыночной процентной ставки и изменение кредитного качества эмитента, определяющего риск потери денег по данному вложению.
Процентный риск возникает в результате неблагоприятного движения (изменения) процентных ставок [7]. Этот вид риска может служить источником сверхприбыли. Однако принятие высокого уровня этого вида риска может сильно влиять на эффективность инвестиций в инструменты с фиксированной доходностью.
Ситуация не является столь очевидной, если речь идет об инвестициях в «долги» на срок, равный сроку оставшемуся до их полного погашения. А именно, если процентные ставки до момента выплаты возрастают, то можно лишь говорить об упущенной выгоде (недополученном проценте). С другой стороны, если «покупка» будущего платежа при фиксированной, оговоренной сегодня ставке осуществляется за счет займа под плавающий (пересматриваемый) процент, то рост такового может привести к отрицательным финансовым результатам (убыткам). Напротив, снижение уровня процентной ставки, позволит в данном случае «сэкономить» на обслуживании займа, и как следствие – получить более высокую прибыль.
Более того, процентная ставка влияет на приведенную к определенному моменту стоимость будущей выплаты. Таким образом, результат купли-продажи долга по теоретической стоимости до момента его погашения складывается из, собственно самого процента за период держания, и из прироста его приведенной стоимости в результате колебания процентной ставки.
Рассмотрим следующую ситуацию: ставка процента (стоимость денег за единицу времени) r на данный момент времени определена однозначно и не зависит от срока заимствования. По истечению времени t будет осуществлена выплата в размере F. При этом полностью отсутствует риски неплатежа, как по срокам, так и по объему.
При сделанных допущениях, текущая стоимость F, в рамках концепции временной стоимость денег, будет определяться по {bd.1}.

В отношение {1.1} справедливы следующие утверждения*(1):
- Во-первых: рост ставки процента r приводит к снижению текущей стоимости будущего платежа, и наоборот, если ставка процента r снижается, то растет приведенная стоимость. Наоборот, если P соответствует рыночной оценке текущей стоимости платежа F, то более высокой P будет соответствовать меньшая ставка процента (в отношении облигаций: доходность к погашению), а меньшей P — большая ставка.
- Во-вторых: если ставка процента (доходность) не меняется до погашения обязательства, то при приближении к моменту выплаты значение P приближается к F. И в момент погашения, P равняется F.
- В-третьих: если ставка процента (доходность) не меняется до погашения обязательства, то разница между F и P уменьшается тем быстрее, чем меньше срока остается до платежа.
- В-четвертых: в каждый момент времени увеличение доходности на определенную величину приведет к уменьшению текущей стоимости на меньшую величину, чем ее прирост, при снижении доходности на ту же величину.
Таким образом, если рассматривать текущую стоимость, как функцию процентной ставки, то приращению аргумента будет соответствовать приращение текущей стоимости, согласно {bd.2}. То есть приращение текущей стоимости со знаком «минус» прямо пропорционально произведению, собственно самой стоимости, времени до выплаты и коэффициенту дисконтирования для «единичного» интервала времени.

Классическую облигацию – облигацию с постоянным купоном – можно рассматривать как портфель, состоящий из дисконтных облигаций: каждый купон – дисконтная облигация, номиналом, равным ставке купона, и отдельно сумма основного долга. Формально, текущая стоимость потока платежей по классической облигации описывается формулой {bd.3}.
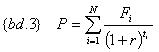
Зависимость приращения текущей стоимости рассматриваемого потока платежей от приращения процентной ставки определяется по {bd.4}.

Введем следующее обозначение – обозначение доли приведенной стоимости i-го платежа в текущей стоимости потока платежей:
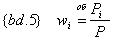
При этом заметим, что:
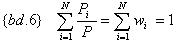
Тогда {1.4} перепишем в более удобном виде:
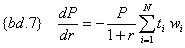
То есть, как и в случае с дисконтной облигацией — {bd.2}, приращение текущей стоимости потока платежей (что соответствует классической облигации или портфелю дисконтных и(или) классических облигаций) со знаком «минус» прямо пропорционально произведению, собственно самой текущей стоимости (приведенной стоимости портфеля), коэффициенту дисконтирования для «единичного» интервала времени, и средневзвешенному сроку платежей.
Дюрацией Маколея, или просто: Дюрацией (Macaulay duration, разработана и предложена Фредериком Маколеем в 1938) – называется средневзвешенный срок платежей по облигации – обозначение {bd.8} – исторически, одна из первых мер процентного риска облигаций.
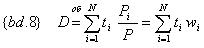
Отметим ряд свойств Дюрации Маколея:
- Во-первых: Дюрация любой купонной облигации не превышает срока до ее погашения, Дюрация облигации с нулевым купоном (дисконтной) совпадает со сроком ее до погашения.
- Во-вторых: если купонная ставка отлична от нуля, то между ставкой процента (требуемой доходностью) и Дюрацией существует обратная связь.
- В-третьих: если до погашения облигации остается более одного купонного платежа, то чем выше купонная ставка при неизменной ставке процента (требуемой доходности), тем меньше Дюрация.
- В-четвертых: чем меньше времени остается до погашения облигации при прочих неизменных факторах, тем меньше Дюрация.
Имея рассчитанную Дюрацию Маколея можно вычислить модифицированную Дюрацию:
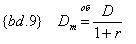
Таким образом, с помощью модифицированной Дюрации можно оценить колебания цены облигации при малых изменениях процентной ставки. На практике, для оценки колебаний текущей стоимости облигации (портфеля облигаций), при предполагаемом изменении процентной ставки применяют следующее приближение:
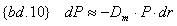
Выпуклость (Convexity) – свойство цен на облигации меняться ассиметрично, относительно изменения доходности. В типичном случае цена облигации возрастет больше при заданном сокращении доходности, чем уменьшение при таком же росте доходности [2 стр. 969].
Выпуклость (Convexity) – мера изменения Модифицированной Дюрации при изменении процентной ставки [8].
С математической точки зрения выпуклость является отношением второй производной текущей стоимости потока платежей к его стоимости: Рассчитать этот показатель можно, согласно {bd.11}, по формуле {bd.12}.

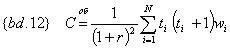
На практике для получения более точной оценки изменения текущей стоимости потока (цены облигации, или портфеля облигаций), по сравнению с {bd.10}, используют {bd.13}:
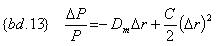
Таким образом, выпуклость позволяет более точно рассчитать изменение цены при малых изменениях требуемой доходности. Хороший обзор теории Дюрации и выпуклости можно найти в [1].
Пример: Облигация казначейства США с датой погашения 15 июня 2017 года и полугодовым купоном 8.875% годовых, текущей стоимостью, приблизительно 128.1231%, доходностью к погашению, в соответствии с принципами SIA*(2) — 5.228% годовых. Дата оценки 15 июня 2007 года.
Ближайший купон будет выплачен 15 декабря 2007 года, то есть о его выплаты осталось ровно одно «полугодие» — один период для начисления сложного процента. Текущая стоимость ближайшего купона:
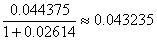
Доля текущей стоимости ближайшего купона в текущей стоимости облигации составляет 0.033479. Взвешенный срок платежа по нему также равен 0.033479 полугодия.
Следующий купон (второй по счету, начиная с даты оценки): срок до выплаты 2 полугодия. Его текущая стоимость:

Доля данного купона в текущей стоимости облигации 0.032889. Взвешенный срок платежа по данному купону 0.032889*2=0.065778.
И так далее …
Последний купон и основной долг: срок до выплаты 20 полугодий. Текущие стоимости:
Купон:
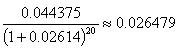
Основной долг:

До платежа последнего купона и основной суммы 0.02067 и 0.4659, соответственно. И взвешенные сроки выплат: 20*0.02067=0.413393 по купону, и 20*0.4659=9.317995 по основному долгу.
Теперь, просуммировав взвешенные сроки всех платежей, получим средневзвешенный срок платежа по облигации, то есть значение Дюрации Маколея – 14.46982 полугодий, или 7.234911 лет.
______________________________________________________
*(1) в [2 стр. 456] со ссылкой на [3] данные утверждения приводятся как «теоремы, связанные с оценкой облигаций.
*(2) SIA (Securities Industry Association) Semi-Annual Yield Conventions [6].
Литература:
1.Ливингстон Г. Дуглас. Анализ рисков операций с облигациями на рынке ценных бумаг. М: Информационно-издательский дом «Филинъ», 1998.
2.Шарп У., Александер Г., Бэйли Дж. Инвестиции: Пер. с англ. – М: ИНФРА-М, 2001. – XII, 1028 с.
3.Burton J. Makliel, “Expectation, Bond prices, and the Term Structure of Interest Rates”, Quarterly of Economics, 76, no 2 (may 1962), pp. 197-218.
4.Bertocchi M., Giancometti R., Zenios S. Risk factor analysis and portfolio immunization in the corporate bond market. 2000, November 2.
5.Fabozzi, Frank J., and T. Dessa Fabozzi, eds. The Handbook of Fixed-Income Securities. Burr Ridge, IL: Irwin. 4th ed., 1995, ISBN 0-7863-0001-9.
6. Mayle, Jan. Standard Securities Calculation Methods. New York: Securities Industry Association, Inc. Vol. 1, 3rd ed., 1993, ISBN 1-882936-01-9. Vol. 2, 1994.
7.Principles for the Management and Supervision of Interest Rate Risk. Basel Committee on banking Supervision. 2001. January. Материалы сайта http://www.bis.org/
Документация к ПО:
8.MATLAB: Financial toolbox documentation — Pricing and Computing Yields for Fixed-Income Securities// Mathworks Software http://www.mathworks.com/
Интернет ресурсы:
9.Bonds Screener //Материалы сайта http://www.finance.yahoo.com/

















