Облигации: мифы и реальность. Часть 3 Глава 4.3
продолжение, начало здесь
удобнее читать в telegra.ph

Инвесторы могут приобретать облигации в качестве альтернативы вкладу в банке, ради извлечения спекулятивного дохода или чтобы припарковать временно свободные средства. А иногда им требуется определенная сумма для выплаты долга или необходимо произвести ряд платежей в погашение ипотеки.
Методы подбора облигационных портфелей таким образом, чтобы обеспечить на заданном горизонте доходность не меньше целевой, носят общее название стратегий иммунизации. Целевая доходность рассчитывается для сценария неизменных форвардных ставок.
В случае плоской КБД форвардные и спотовые ставки равны единой и постоянной во времени (эффективной) ставке дисконтирования r(t) = const. Как обсуждалось в прошлых частях, при этих условиях мы можем гарантировать исполнение номинального обязательства L (liability) через T лет, если приобретем портфель облигаций A (assets), стоимость P0[r] которого будет равна приведенной стоимости PV(L):
P0[r] = PV(A) = PV(L) = L /(1+r)ᵀ
В качестве аналога можно привести депозит с капитализацией процентов — клиент точно знает сколько получит при его закрытии. Но в отличие от депозита, срок погашения для облигаций в портфеле не обязан совпадать с T. Важно, что через это время стоимость портфеля станет равна L, т.е. мы можем его продать, чтобы выплатить долг.
Рассмотрим простой пример, когда в экономике действуют номинальные годовые ставки в 10% с полугодовым начислением процентов, т.е. ставка за период (полугодие) равна 5%. Тогда для получения накопленной стоимости 1 млн руб. через 3 года нам потребуется внести на депозит в банке сумму 1 млн/ (1+(10/2)%)² × ³ = 1 млн/ (1+5%)⁶ = 746215 руб. Или можно сначала рассчитать эффективную годовую ставку r = (1+5%)² -1 = 10.25% и получить ту же сумму: 1 млн/(1+ 10.25%)³ = 746215 руб. Десятилетняя облигация с купоном 7% годовых при номинальной доходности 10% будет стоить на рынке ≈ 813 руб. (для выполнения расчета в Excel все цифры необходимо привести к одному периоду, полугодию — PV(5%,20,35,1000)) Если мы приобретем 746215/813 ≈ 918 таких облигаций, то через три года они дадут накопленную стоимость 1 млн руб., что легко проверить расчетами (определив цену облигаций на горизонте 3 лет и инвестируя ранее полученные купоны в те же облигации)
Когда спотовая кривая не является плоской, неизменность форвардных ставок означает, что ее эволюция соответствует “предсказаниям” теории чистых ожиданий (будущие спотовые ставки равны текущим форвардным)

Как следует из предпосылок этой теории, инвестору должно быть всё равно какую облигацию купить, — годичную, трехлетку или десятилетку, — так как если ожидания рынка, “зашитые” в кривой доходности, оправдаются, то все облигации дадут одинаковый HPR в конце периода. Ситуация останется прежней через год, два и так далее. А значит стоимость портфеля облигаций все время будет равна приведенной стоимости обязательства вплоть до срока его уплаты. Подробное доказательство этого факта можно найти у Ю-Дау Люу в книге “Методы и алгоритмы финансовой математики”
Рассмотрим пример для семейства кривых, указанных на анимированном графике. Будущие спотовые ставки можно найти по формулам из главы 4.2.1, расчёты приведены в приложенном файле Excel. Допустим, мы имеем обязательство L номинальной стоимостью 100 ден. единиц и сроком исполнения через 5 лет. Его приведенная стоимость PV(L) = 100/(1+s₅)⁵ = 100/(1+15.62%)⁵ = 48.41. Десятилетняя бескупонная облигация будет торговаться по 100/(1+s₁₀)¹⁰ = 100/(1+17.64%)¹⁰ = 19.7 ден. ед. Если приобрести 48.41/19.7 = 2.46 таких облигаций, то стоимость портфеля A через 5 лет составит (10-летка станет 5-леткой) 2.46∙100/(1+ s*₅)⁵ = 2.46∙100/(1+ 19.7%)⁵ = 100 ден. ед, что в точности покрывает обязательство L. Будущая 5-летняя спотовая ставка s*₅ получена в предположении, что эволюция КБД следует теории чистых ожиданий.
Таким образом, если динамика будущих ставок жестко детерминирована, для достижения цели инвестору достаточно выполнить условие PV(L) = PV(A) в момент покупки облигационного портфеля A.
Во всех остальных случаях невозможно точно рассчитать будущую стоимость процентных бумаг на любой наперед заданный момент времени. Основными драйверами неопределенности выступают ценовой риск и риск реинвестирования, и с ними надо как-то бороться.
Иммунизация единичного обязательства. Плоская КБД.
Когда в одной из прошлых частей цикла мы рассматривали однократные сдвиги плоской кривой доходности, то выяснили, что покупатель, заинтересованный в получении целевой накопленной стоимости, выбирает портфель с дюрацией Маколея равной его горизонту инвестирования. Обсудим этот вопрос немного подробнее.
В финансовой литературе и на популярных сайтах часто можно встретить интерпретации дюрации Маколея как некоего “центра тяжести”:
“Наиболее простое объяснение сути дюрации — это представление финансовых потоков как грузиков, расположенных вдоль стержня (временной оси), находящегося в равновесии на одной точке опоры. Длина стержня — срок до погашения. Дюрация — длина участка от левого края стержня до точки опоры. Расстояние между грузиками — купонный период”
“Дюрация — это точка опоры, уравновешивающая все дисконтированные платежи по облигации”
Эти дисконтированные платежи схематично указаны столбиками в примере на рисунке ниже; “вес” каждого последующего купона уменьшается, последняя выплата включает номинал облигации.
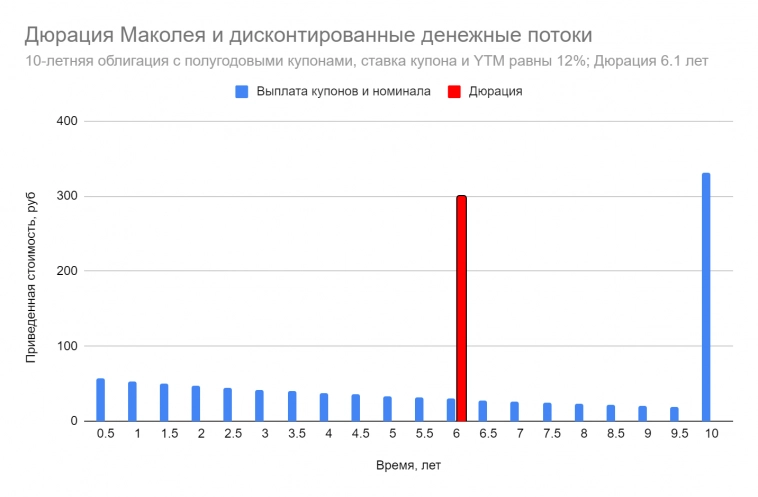
Действительно, если мы изготовим гирьки с весами, равными приведенным стоимостям денежных потоков, и поместим их на линейку в соответствующем порядке, то центр масс всей системы окажется как раз в “точке дюрации” Это следует из его определения как оно вводится в любом школьном учебнике по физике.
Точка на оси абсцисс, соответствующая центру масс невесомого продольного стержня с грузиками:
x꜀ = Σ mₖ·xₖ/M, где mₖ — массы грузиков, xₖ — их координаты, М = Σ mₖ — общая масса системы. В определении дюрации Маколея весам соответствуют приведенные стоимости денежных потоков Cₖ — PV(Cₖ), координатам — сроки до погашения Tₖ, общей массе — стоимость портфеля облигаций.
Поможет ли формальный перенос понятий из курса механики лучше представить, для чего именно нужна дюрация Маколея? Рассчитав центр тяжести, мы знаем как обустроить скамейку или обеспечить поступательное движение тела. Но в случае облигаций нам потребуется уже другая трактовка и про грузики-купоны лучше окончательно забыть. Гораздо удобнее считать, что на горизонте равном дюрации Маколея в равновесии находятся не дисконтированные платежи, а риски портфеля: ценовой и реинвестирования, точнее, их совместное влияние на накопленный доход. Мы предполагаем, что эти риски могут реализоваться в любой момент после приобретения облигации. Когда мы находимся в начале пути и определяем свой горизонт (т.е. анализируем, что будет, если продать бумаги через полгода, год, пять лет), то чем меньше предполагаемый срок удержания, тем выше риск изменения цены. Он исчезает на горизонте совпадающим с датой погашения облигации. И на этом же горизонте максимальным становится риск реинвестирования, который не имеет значения при краткосрочных вложениях.
Дюрация Маколея дает нам точку безразличия в результате однократного сдвига плоской кривой доходности. Она равна количеству времени, необходимому, чтобы первоначальные изменения как цены, так и ставки реинвестирования полностью компенсировали друг друга.
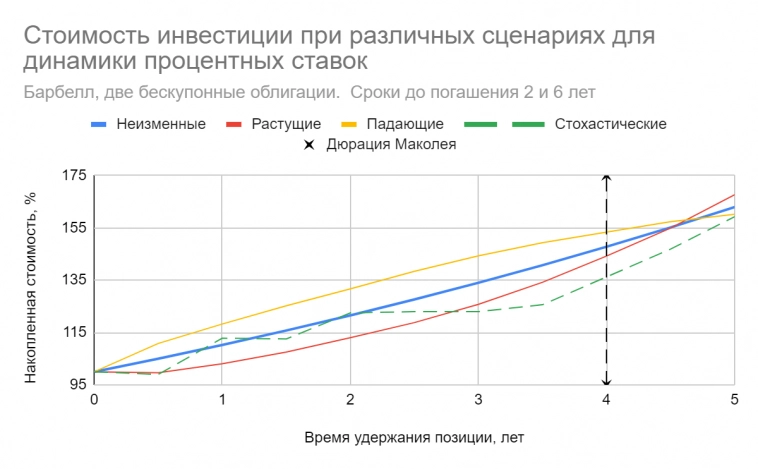
На рисунках ниже приведены примеры портфелей, иммунизированных для достижения целевой накопленной стоимости ≈ 148 ден. единиц на горизонте 4-х лет: пятилетняя облигация номиналом 100 ден. ед. и ставкой купона около 11% (точное значение 10.96%) годовых, и “барбелл” из двух бескупонных облигаций — со сроками погашения 2 и 6 лет. Двухлетка роллируется через каждые два года. Номинальная доходность к погашению (YTM) в момент покупки портфелей составляет 10% годовых, сразу после этого она может измениться на ±50 б.п. Бумаги взяты в “количествах”, обеспечивающих начальную стоимость в 100 ден. единиц для каждого портфеля, что совпадает с приведенной стоимостью обязательства — 147.75/(1+5%)⁸ = 100. Например, пятилетних облигаций всего имеется 0.964 штук. Понятно, что дробных облигаций не бывает, но это просто вопрос масштабирования относительно размера вложенных средств, т.е. на миллион необходимо приобрести 9640 таких бумаг. Дюрации Маколея обязательства и обоих портфелей равны 4 годам.
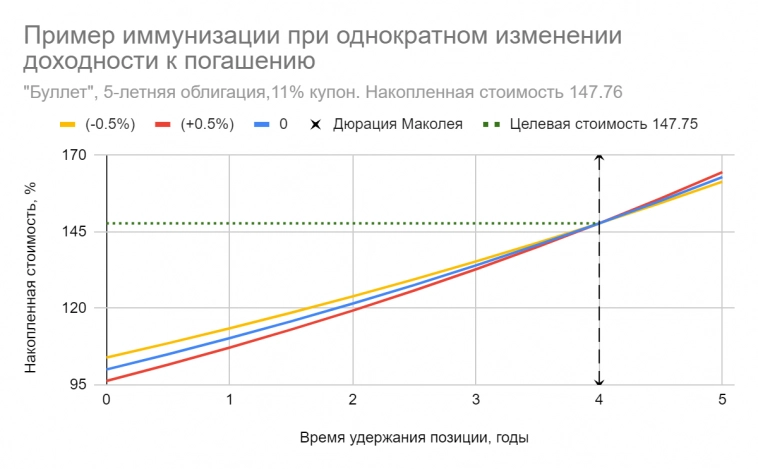
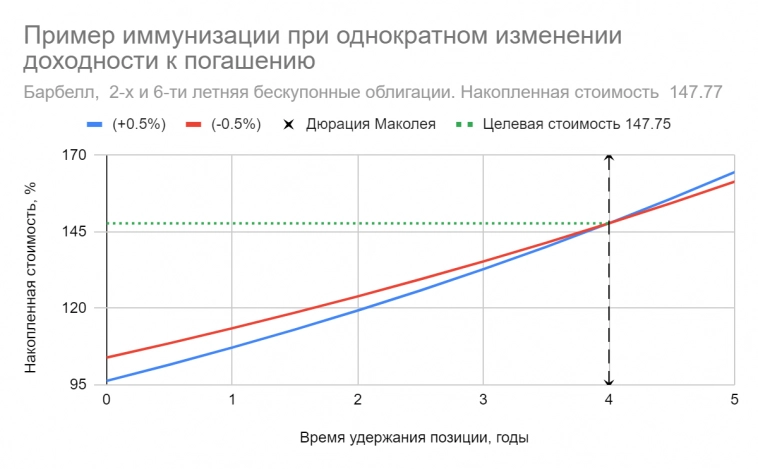
Видно, что если сдвиг кривой доходности происходит единожды, реализованная накопленная стоимость не меньше планируемой. Выбрав любой портфель A с приведенной стоимостью PV(A) = PV(L) и дюрацией Маколея D(A) = D(L) = T (срок погашения обязательства, горизонт инвестирования), инвестор достигнет поставленной цели. При прочих равных лучше сработает иммунизированный портфель, имеющий большую выпуклость. В нашем примере это “барбелл”, и его накопленная стоимость после единичных сдвигов КБД чуть выше, чем у “буллета”. В литературе зачастую приравнивают не дюрации Маколея, а модифицированные дюрации DM =D/(1+rₚ), где rₚ — периодическая доходность к погашению. Для случая плоской КБД разницы в выборе нет, так как доходности yₚ как портфеля, так и обязательства будут все время равны. Однако целевая стоимость достигается именно на горизонте, совпадающим с дюрацией Маколея.
В реальной жизни ставки имеют свойство постоянно изменяться с течением времени. Посмотрим как поведут себя оба портфеля в случае различной динамики плоской КБД, если мы не будем менять их структуру на протяжении удержания позиции (выплаты по купонной облигации вкладываются в ту же бумагу, короткая бескупонная облигация роллируется)
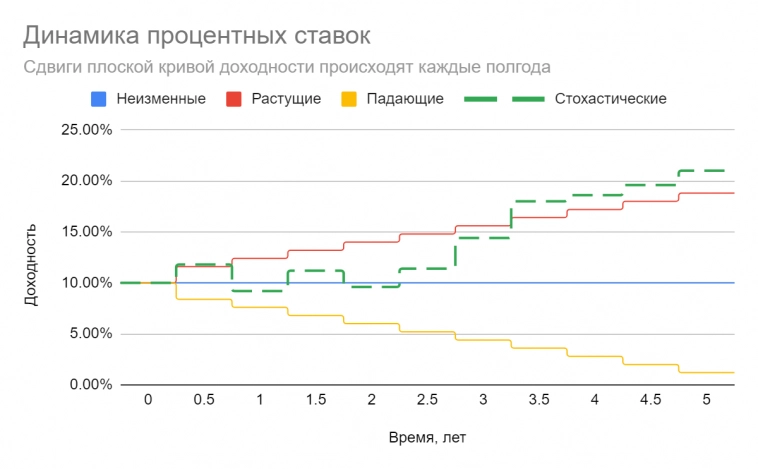
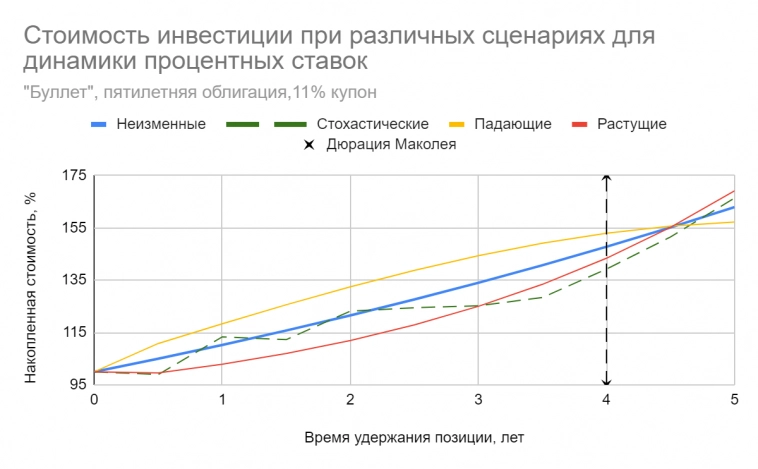
Можно заметить следующее:
1) Во всех случаях многократного изменения ставок накопленная стоимость на горизонте 4-х лет будет различна и не равна целевой сумме, т.е. ≈ 148 ден. единиц.
2) На этом же горизонте у “барбелла” разброс в значениях накопленной стоимости может быть сильнее, чем у “буллетного” портфеля.
3) Реализованная накопленная стоимость будет меньше целевой в случае растущих ставок, и наоборот — больше целевой, если ставки имеют тенденцию к снижению.
Первое наблюдение объясняется тем, что с течением времени дюрации иммунизированного портфеля A и обязательства L уменьшаются с разной скоростью. Это происходит даже в том случае, если ставки не меняются. Обязательство — это аналог бескупонной облигации, и его дюрация Маколея всегда равна оставшемуся сроку до погашения. Дюрация купонной облигации снижается медленнее, так как у такой бумаги срок погашения больше, чем у бескупонной той же дюрации. На рисунке ниже облигация A и обязательство L поначалу имеют одинаковую дюрацию Маколея, равную 8 годам. График дюрации облигации А имеет пилообразный вид, так как мы учли межкупонный период. С уменьшением срока до погашения расхождение дюраций растёт несмотря на отсутствие изменений в доходности.
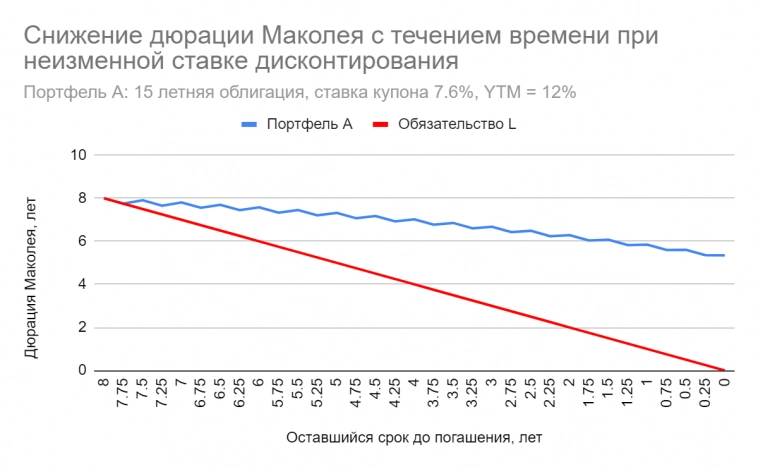
Второй факт связан с тем, что у “барбелла” выше риск реинвестирования. Короткая бумага при роллировании оказывает куда большее влияние на накопленную стоимость по сравнению с относительно небольшими суммами купонов в “буллетном” портфеле. Результат в 3) объясняется превалированием ценового эффекта при длящейся тенденции изменения ставок.
Иммунизация портфеля облигаций — не разовое действие, т.е. она не будет работать сама по себе в рамках парадигмы “купил и держи”. Это требующий корректировок процесс, и портфелю A необходима периодическая ребалансировка даже при неизменных ставках, чтобы обеспечивать равенство D(A) = D(L) Ведь мы не знаем, когда именно произойдет следующий сдвиг КБД и должны быть к нему готовы по мере сил.
На рис. ниже указан пример динамической иммунизации “буллетного” портфеля при стохастических изменениях ставок. Для поддержания равенства дюраций структура портфеля каждые полгода изменяется: часть бумаг продается для приобретения краткосрочных инструментов (например, полугодовых банковских депозитов)
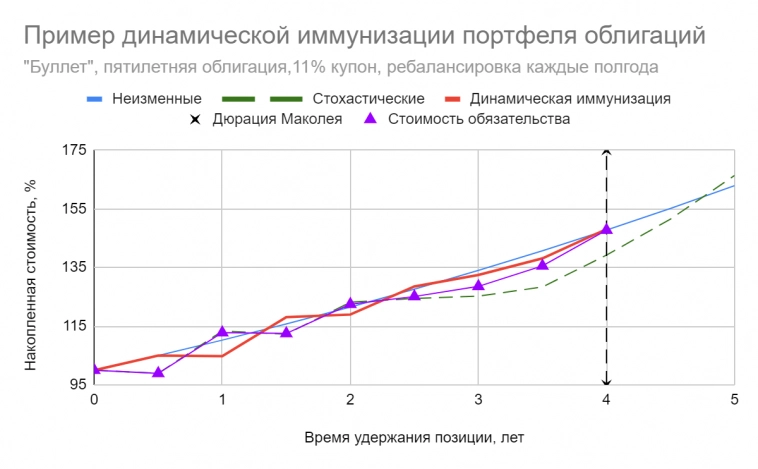
Постепенно все облигации будут “израсходованы” и через четыре года у инвестора на руках окажутся только наличные. Изменения стоимости обязательства L и динамически иммунизированного портфеля A поначалу идут в “противофазе”, но затем колебания сглаживаются. Реализованная накопленная стоимость (148.09) будет чуть выше, чем целевая (147.75), что является заслугой выпуклости, т.к. C(A) > C(L)
В нашем модельном расчете ребалансировка происходит сразу после выплаты купонов и непосредственно перед очередным скачком уровня ставок, поэтому результат выглядит столь впечатляюще. Причем, в этом сеттинге реализованная накопленная стоимость всегда будет больше целевой, независимо от конкретной траектории случайного процесса, описывающего динамику плоской КБД. Ниже представлен результат симуляции Монте-Карло в дискретном аналоге модели CIR с параметром волатильности 2% и возвратом к “средней” полугодовой ставке 5%. Сами расчеты приведены в файле Excel.
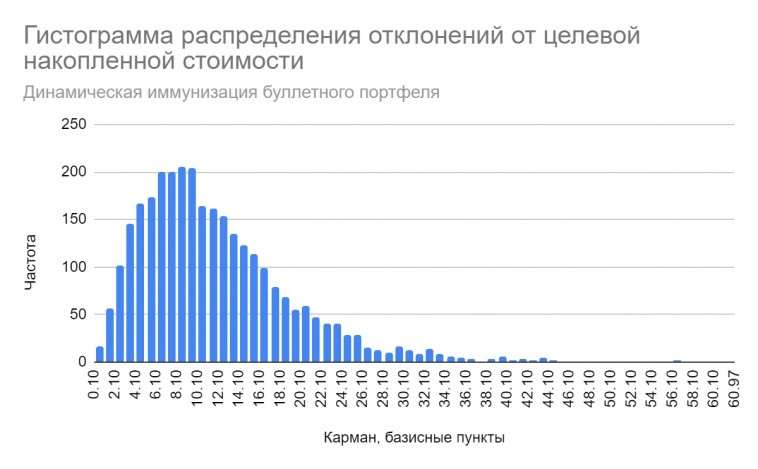
Видно, что распределение относительных смещений от целевой стоимости (RealizedValueₖ — 147.75)/147.75 имеет очень небольшой разброс, а все значения отклонений положительны. Можно сравнить эти данные с вариантом, когда динамическая иммунизация не проводится, т.е. однажды иммунизированный портфель в дальнейшем предоставлен самому себе:

Примерно в половине случаев однократная иммунизация провалится, а для некоторых траекторий ставок “недобор” целевой стоимости на горизонте 4-х лет превысит 10%.
Но, конечно, более корректным будет сравнение результатов динамической иммунизации с колебаниями будущей стоимости облигации, у которой срок погашения равен горизонту инвестора, т.е. в нашем случае 4-м годам:
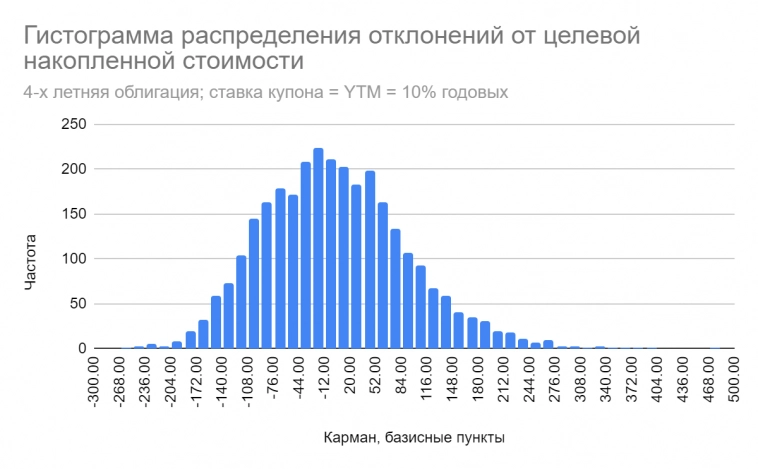
Диапазон отклонений в этом случае гораздо уже, в среднем ± 100 б.п., но все же с вероятностью около 50% инвестор не сможет исполнить обязательство.
Понятно, что в реальной жизни КБД не будет терпеливо ждать, пока инвестор подгонит свой портфель под новое соотношение дюраций. Чем чаще проводится ребалансировка, тем точнее портфель A будет следовать извилистым путям обязательства. С другой стороны, каждое изменение структуры портфеля повлечет за собой дополнительные расходы на уплату комиссионных брокеру и бирже. А значит, необходим какой-то компромисс при выборе частоты ребалансировки. На практике дюрация корректируется сразу после выплаты очередного купона, так как при неизменных или слабо меняющихся ставках портфель остается иммунизированным вплоть до даты следующего платежа (это следствие пилообразного характера дюрации, см. рисунок выше)
Активно управляемый портфель пытается воспроизвести бескупонную облигацию, т.е. стать “зеркальным отражением” обязательства. Знатоки деривативных инструментов, наверное, уже заметили, что динамическая иммунизация напоминает процесс дельта-хеджирования, когда банк хеджирует короткую опционную позицию с помощью базового актива и безрискового долгового инструмента, чтобы создать реплицирующий портфель для проданного опциона. Такая аналогия отчасти справедлива, ведь денежная дюрация (произведение модифицированной дюрации и цены) имеет смысл дельты облигации, а денежная выпуклость — ее гаммы.
окончание в следующей статье













