Биржевое распределение вероятностей
Кто не первый день торгует на бирже, тот знает, что для описания вероятностных процессов происходящих на биржевых торгах не подходит формула нормального распределения вероятностей (распределение Гаусса). Рассмотрим нормальное распределение вероятностей (НР) и биржевое распределение вероятностей (БР).
Нормальное биржевое распределение
Первое отличие БР от НР заключается в том, что БР имеет более «толстые хвосты». То есть, немного большая часть вероятностных событий находится дальше от точки математического ожидания. Этот факт можно объяснить тем, что в НР {\displaystyle \sigma } б — среднеквадратическое отклонение (волатильность) является константой, а в БР волатильность величина переменная и тоже случайная. Наличие своей дисперсии у волатильности дает нам дополнительное «размазывание» плотности вероятностей.
Возьмем формулу нормального распределения:
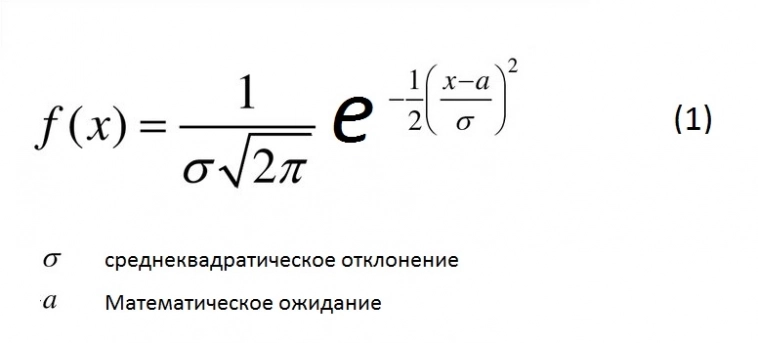
Поскольку б (среднеквадратическое отклонение) для БР переменная, то логично было бы представить ее в виде функции, либо добавить к текущему значению б «функцию размытия» r(x, б). Тогда для биржевого распределения будем иметь формулу следующего вида:
Функция размытия r(x, б) должна быть такой, чтобы итоговая функция:
— была близка по форме к нормальному распределению
— имела более толстые хвосты
— площадь ограниченная графиком должна быть равна 1 ( сумма всех вероятностей равна 1)
Существует такая функция удовлетворяющая вышеперечисленным условиям:

Подставляя (3) в (2) получим функцию распределения вероятностей на основе нормального распределения, но с более толстыми хвостами. Назовем ее «биржевое нормальное распределение» (БНР)
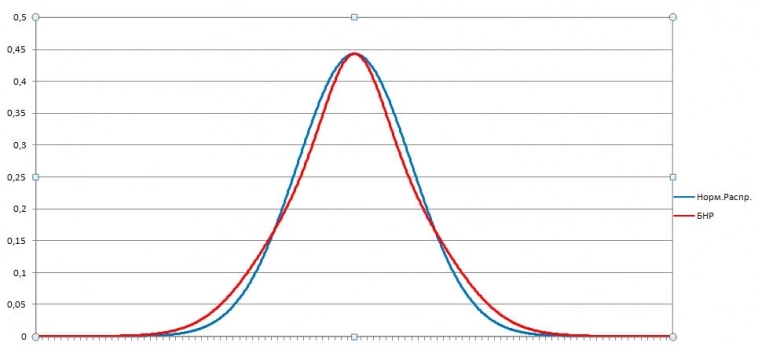
Полученное распределение показывает, что вероятность распределена в виде узкого канала, либо идет смещение в сторону начавшегося тренда. То есть возможность получения прибыли лежит в работе внутри канала, либо в следовании тренду.
«Логнормальное» Биржевое распределение
В реальной торговле (например, акциями) у нас не бывает отрицательных цен. Изменение цены актива в меньшую сторону (приближение к нулю) приводит к уменьшению дисперсии, выраженной в абсолютных величинах. Изменение цены с 1 рубля до 2 рублей в относительных величинах будет равно 100%, но в абсолютных изменение будет всего на 1 рубль. В вышеприведенных формулах используются абсолютные значения дисперсии. Поэтому нам необходимо учесть уменьшение дисперсии в зависимости от уменьшения цены. Обычно для таких целей используют логарифмическую зависимость. Но такая задача гораздо легче решается с помощью квадратного корня.
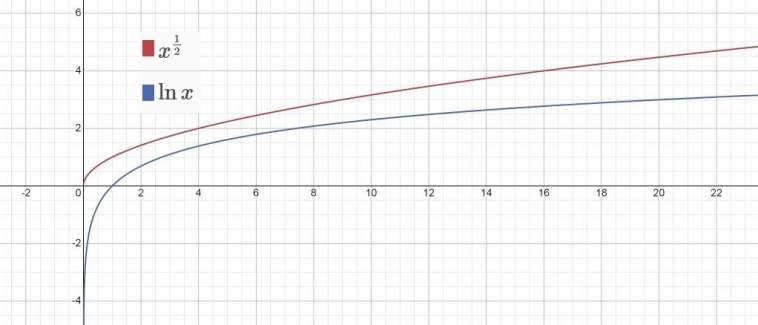
Для этой цели б (среднеквадратическое отклонение) умножается на функцию сжатия дисперсии L(x,a)=(х/a)^0.5
Полностью формула биржевого распределения вероятностей выглядит следующим образом:
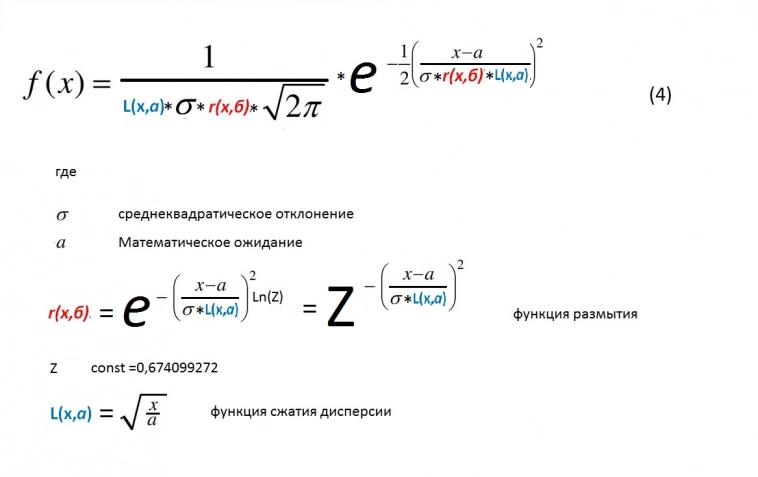
В сравнении с логнормальной функцией распределения она выглядит следующим образом:
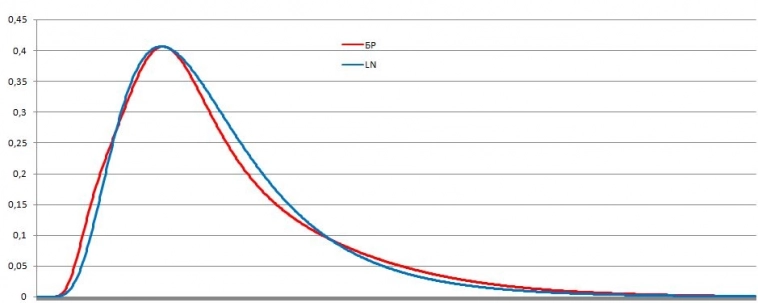
LN – логнормальное распределение; БР – распределение по формуле (4)
В данном случае, мы так же видим более толстые хвосты, чем у обычного логнормального распределения. Полученная формула является более подходящей для описания распределения вероятностей при торговле на бирже. Но в дальнейшем, данная формула требует обкатки в реальных условиях.














Если мы спекулянты, то мы работаем с конкретной реализацией процесса на коротком интервале времени, где вид распределения тоже ни о чем и не дает нам никакой информации для сделки (сделок).