Оценка бессрочных облигаций, и как это может помочь при оценке вечного фьючерса на USDRUB
Обратил внимание, что многие не знают, как правильно оценить вечную облигацию. Однако, ее оценка существенно проще, чем оценка обычных облигаций. Давайте разберемся, как можно оценить бессрочную облигацию.
Как мы знаем внутреннюю (приведенную стоимость) облигации можно оценить с помощью следующей формулы потока платежей: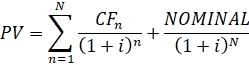
Где:
CFn – купоны
NOMINAL – сумма, которую получит инвестор при погашении облигации
i – ставка доходности
n – год получения купона
N – последний год
PV – приведенная стоимость облигации
В бессрочной облигации нет погашения номинала – NOMINAL, и количество платежей бесконечно, тогда формула принимает вид:
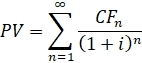
Для простоты предположим, что мы имеем дело с бессрочной облигацией с постоянным купоном. Тогда CFn=CF, а формула примет вид:
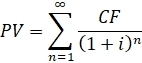
Теперь сделаем несколько преобразований:
1. Для начала умножим обе части на (1+i) и получим:
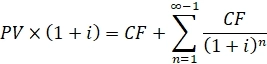
2. Вычтем из первого выражения второе:
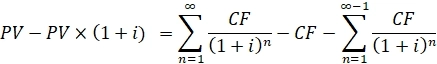
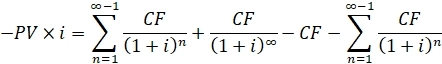
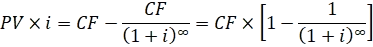
3. Так как:
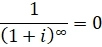
Получаем:
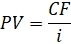
Смотря на эту формулу, получается интересный вывод: i – для бессрочной облигации одновременно является текущей доходностью и «доходностью к погашению» (термин – который используется в облигациях). Иными словами, используя ее мы можем либо найти приведенную стоимость облигации, либо определить то, что называют «доходность к погашению», хотя формально это облигация никогда погашена не будет.
Те, кто знает, как правильно инвестировать в облигации, представляют, что кроме доходности к погашению, хорошо бы посчитать еще три показателя: дюрацию Маколея, модифицированную дюрацию и выпуклость(кривизну).
Здесь я выводы приводить не буду, а просто дам готовые формулы.
Давайте разберем пример. Пусть у нас есть бессрочная облигация с «доходностью к погашению» в 8.92%. Необходимо рассчитать, как измениться ее цена если процентные ставки параллельно пойдут вниз на 2 процентных пункта. И через сколько лет поток мы получим эффект иммунизации?
Модифицированная дюрация для такой облигации будет:
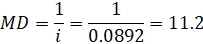
Считаем изменение цены облигации:
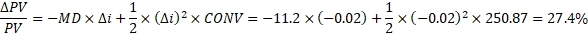
Таким образом цена облигации вырастет на 27.4%.
Эффект иммунизации проявится через 12.2 года:
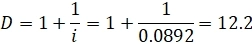
Зная принципы расчетов параметров бессрочных облигаций, можно не только эффективно инвестировать в них, управлять дюрацией портфеля, но также рассчитывать, например, теоретическую стоимость фьючерсов.
Недавно московская биржа запустила торговлю вечным фьючерсом на валюту, и одним из вопросов, который стоит перед инвесторами, какая же должна быть теоретическая стоимость фьючерса. Напомню, что теоретическая цена простого контракта рассчитывается по формуле:
Где:
F – фьючерсная цена
S – спот цена на рынке
i – безрисковая ставка
t – количество дней до исполнения фьючерса
T – база дней в году 360/365
Но контракт USDRUBF не истекает – он все время лонгируется, что делает его бесконечным.
Давайте посмотрим на это с другой стороны.
Так на конец 9 июня 2022 стоимость бессрочного контракта USDRUBF была 64,33, в то время как спот цена доллара на рынке составила 59,25 рублей. Это значит, что цена фьючерса была на 8,57% выше. Используем формулу дюрации Маколея для бесрочных облигаций и для этой ставки:
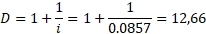
Теперь сравним этот результат с теми доходностями, которые мы видели на ОФЗ 9 июня 2022, для чего построим кривую доходности ОФЗ. Уравнение кривой на графике.
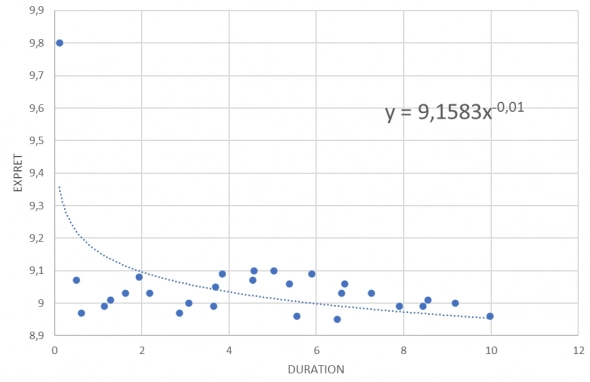
Теперь рассчитаем какова доходность ОФЗ для дюрации 12.66:
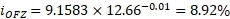
Формально получается, что доходность ОФЗ выше, чем 8.57% заложенная во фьючерсе, а значит можно сказать, что его цена даже мала, хотя в условиях таких расчетов 0.4% можно считать несущественной и признать, что фьючерс оценен справедливо (кстати, чисто математический расчет даст нам дюрацию облигации в 730 лет, которая будет соответствовать 8.57%, конечно это связано с функцией, которую мы использовали для апроксимации). Вот так, можно оценить справедливость стоимости бессрочного фьючерса.
Однако, для валюты есть существенный нюанс. Теоретическая цена валютного фьючерса учитывает две безрисковые ставки:
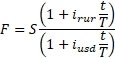
Где:
F – фьючерсная цена
S – спот цена на рынке
irur – безрисковая ставка в рублях
iusd – безрисковая ставка в долларах США
t – количество дней до исполнения фьючерса
T – база дней в году 360/365
И в таком варианте ситуациям усложняется.
Буду рад Вашим замечаниям и предложениям.

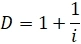
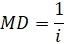
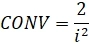
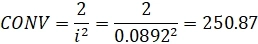
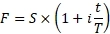












Это залёт, Алёша.
Господа, сорри за оффтоп, но вы здесь обсуждаете фьючерсы, а у меня как раз вышла дилемма с фьючом на Брент.
Не могли бы подсказать?
Вопрос по расчету вармаржи по фьючерсу на нефть.
Допустим, стоимость фьюча BR-7.22 составляет 120, шаг цены — 0,01, стоимость шага – 5,675 (курс доллара – 56,75). Таким образом, стоимость 1 контракта равна (120/0,01)*5,675=68100 рублей.
Пусть цена BR-7.22 выросла до 125, а курс доллара упал до 51. Тогда вармаржа будет отображаться такой: ((125-120)/0,01)*5,675=2837,5 руб. Получается прибыль.
НО! Здесь пересчет происходил по старому курсу доллара. По новому курсу стоимость 1 контракта BR-7.22 равна (125/0,01)*5,100 = 63750 рублей. Т.е. за счет укрепления рубля цена контракта снизилась.
Таким образом, по данной сделке получаем убыток = 63750 – 68100 = -4350 рублей.
Такой вопрос. Правильно ли я понимаю, что в течение торговой сессии в графе «Вармаржа» я буду видеть прибыль в 2837,5 руб, но по итогам клиринга мне начислят убыток в размере -4350 рублей?
Сорри за глупые вопросы