Математика жизни и смерти. Часть 3. 7 математических принципов, формирующих нашу жизнь. Кит Йейтс.

Математика жизни и смерти. Часть 3. 7 математических принципов, формирующих нашу жизнь. Кит Йейтс.

В этом видео разоблачим статистики СМИ.
Разберем регрессию к среднему значению. 

Раскажу про бинарные решения, проблему перебора и пузырьковую сортировку, Задачу о рюкзаке, что такое виртуальным дарвинизм и Стратегия оптимальной остановки.

Разберем эвристические, Жадные, муравьиный алгоритмы и самый известный природный алгоритм – эволюцию. 

Обсудим: Разоблачение статистики СМИ.

Статистику можно подобрать так, чтобы представить определенный взгляд на вещи – и сохранить при этом видимость объективности.

Противоречащие выводу цифры просто игнорируются, и за счет выборочного использования данных искажается реальность. 

Небольшие, нерепрезентативные или предвзятые выборки в сочетании с наводящими вопросами и выборочным представлением данных – вот рецепт недостоверного статистического исследования. 

Есть еще более тонкий прием – использовать статистику вне контекста: 

300-процентный рост заболеваемости может означать и увеличение количества заболевших с одного пациента до четырех, и с 500 тысяч человек до двух миллионов. 

Контекст важен.

Нам остается попытаться собрать воедино истинную историю, стоящую за журналистскими перегибами.

Давайте проанализируем и развенчаем уловки, ловушки и махинации в газетных заголовках, рекламных объявлениях и политической риторике. 

Мы представим простые способы распознать, когда от нас утаивают часть информации. 

Мы познакомимся с инструментами, которые помогут вскрыть манипуляции со статистикой. И в конце концов выясним, когда мы должны верить «правде».

(Парадокс дней рождения).

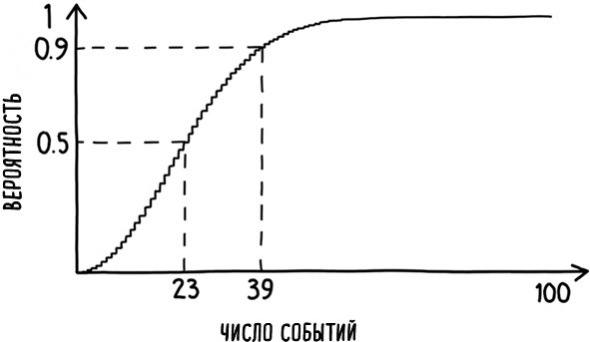
Вероятность наступления двух и более событий в один и тот же день возрастает с увеличением количества событий. 

При наличии 23 событий, например, дня рождения в один день,  вероятность совпадения чуть выше 1/2. 

При наличии 39 независимых событий вероятность того, что в один день произойдут как минимум два из них, возрастает почти до 0,9

(Рис. 16)

если какие-то данные могут свидетельствовать в пользу рекламодателей продукта, эти данные старательно выпячивают. 

Рекламодатели прекрасно знают, что люди, как правило, безоговорочно доверяют цифрам. 

Но эта объективность обманчива.

Так, достоверность представленных в рекламе L’Oreal результатов, которые были получены на выборке всего 34 человека, не может не вызывать определенные сомнения.

В 2009 году под мощным, надо признать, заголовком

 «Легкомысленное поедание свинины убивает» таблоид Sun сообщила об одном из результатов Всемирного фонда исследования рака – о влиянии ежедневного потребления 50 граммов мясных продуктов на развитие раковых заболеваний.

Таблоид шокировал читателей тем «фактом», что один бутерброд с беконом (если есть его каждый день) увеличивает риск рака толстой кишки на 20 %.

Вместо того чтобы использовать более объективный показатель абсолютного риска, Sun решила сосредоточить внимание на относительном риске – 

риске конкретного исхода (например, развития рака) для людей, подвергающихся воздействию определенного фактора риска (например, употребление в пищу бутербродов с беконом) относительно доли риска для популяции в целом. 

Если относительный риск выше единицы, то у человека, подвергшегося воздействию, вероятность развития заболевания выше, чем у человека, не подвергшегося такому воздействию. 

Если же он ниже единицы, то риск ниже. 

исключение из этого уравнения людей, не затронутых болезнью, заставляет прирост относительного риска (6/5 или 1,2) выглядеть гораздо более драматичным.

относительный риск для тех, кто употребляет в пищу 50 граммов мясных продуктов в день, увеличивается на 20 %, абсолютный риск увеличивается только на 1 %. 

Но такая цифра не поднимет продажи газеты. 

Жонглирование цифрами привело к тому, что ученых, которые «объявили войну бекону», несколько дней клеймили в прессе как «нацистов от здорового образа жизни».

Если вы хотите узнать правду, стоящую за заголовками, поищите публикации, предоставляющие абсолютные статистические данные по заинтересовавшей вас проблеме, или даже попробуйте найти ту научную статью, в которой такие данные приведены впервые, – все чаще доступ к таким статьям в интернете можно получить бесплатно.

(Регрессивное отношение).

Вполне возможно, что большинство статистических искажений в медицинском контексте возникает неосознанно – просто исследователи не знают о некоторых распространенных статистических ловушках.

Острота таких расстройств, как боль в суставах, с течением времени колеблется.

Вполне вероятно, что на участие в испытаниях – особенно в таких экстремальных и нестандартных, как апипунктура (лечение укусами пчел), – соглашаются те, кто находится в самом тяжелом положении и отчаянно нуждается хоть в каком-то облегчении своего недуга. 

Если сеанс лечения проводится на фоне острой боли, то через некоторое время они весьма вероятно почувствуют себя лучше – вне зависимости от результативности лечения. 

Это явление называют регрессией к среднему значению. 

бóльшая часть эффекта плацебо может быть вызвана регрессией к среднему.

Есть множество способов извлечь из правды выгоду при помощи математики. 

Статистические данные, которыми оперирует медиа, реклама и политики, часто недостоверны, иногда искажены, но почти никогда не являются полностью неверными. 

В них обычно скрыты зерна истины, но очень редко – истина во всей ее полноте. 

Иногда эти искажения делают злонамеренно, а порой манипулятор и сам не подозревает об ошибках в своих расчетах или о том, что опирается на предвзятые данные. 

рассмотрим катастрофические последствия таких реальных математических ошибок в более громких случаях.

(Глава 5. Не то место, не то время: эволюция систем счисления и их просчеты).

познакомимся с тем, как системы, «пронумеровывающие» нашу повседневную жизнь, приводят к ошибкам, которые очень дорого нам обходятся. 

проследим за естественным отбором наших систем счисления – как они заходят в тупик в своем развитии и как следуют пересекающимися маршрутами вместе с развитием цивилизации.

выявим математическое мышление, которое настолько глубоко укоренилось в нашем подсознании, что мы даже не осознаем, как оно формирует и ограничивает наши интересы.

подавляющее большинство культур, разработавших числовые системы (армяне, египтяне, греки, римляне, индийцы, китайцы и т. д.), выбрали десятичную систему. 

Все просто: когда мы поняли необходимость счета, мы начали использовать для этого пальцы – во многом так же, как учим наших детей считать и сегодня.

некоторые культуры выбрали другие основания, исходя из различных аспектов нашей биологии. 

Индейцы юки, проживающие на территории Калифорнии, ведут восьмеричный счет, используя в качестве маркеров пространство между пальцами, а не сами пальцы. 

Шумеры основанием системы счисления избрали число 60. 

Его они получили, подсчитав 12 суставов четырех пальцев правой руки и откладывая пять раз по 12 (в сумме 60) на пяти пальцах левой руки.

Римляне использовали семь символов:

 I, V, X, L, C, D и M – для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 соответственно. 

Понимая, что их система цифр несколько громоздкая, римляне всегда записывали числа слева направо, от самых больших до самых маленьких, поэтому символы можно было просто сложить вместе.

На фасаде Бостонской публичной библиотеки имеется надпись из 13 знаков – (MDCCCLXXXVIII) – самое длинное римское число за последнее тысячелетие; оно обозначает 1888 год.

Римской математике категорически не хватало концепции позиционной – или пространственной – системы счисления.

Позиционная система счисления позволяет зафиксировать любое число – вне зависимости от его размера – всего несколькими простыми символами. 

В египетской и римской системах положение символа не имело глобального значения. Вместо этого значение числа определялось самим символом.

Возможно, основная причина, по которой шумеры использовали шестидесятеричную систему, заключалась в том, что она значительно облегчала деление и операции с дробями. 

Древние греки, основываясь на шумерской традиции, делили каждый градус на 60 минут и каждую минуту на 60 секунд.

Вообще, слово «минута» означает чрезвычайно маленькую долю (в нашем случае круга), а слово «секунда» – второй уровень деления градуса.

древние египтяне разделили день на 24 сегмента 

12 дневных и 12 ночных часов, повторяя количество месяцев в солнечном календаре. 

При дневном свете время фиксировалось с помощью солнечных часов с 10 делениями. 

Были добавлены два сумеречных часа, по одному в начале и в конце дня – для периодов, когда солнечные часы бесполезны.

Ночь была аналогичным образом разделена на 12 частей, привязанных ко времени восхода определенных звезд на небе.

Строгое деление дня на 12 световых часов заставляло египтян менять длительность каждого дневного часа в течение года в зависимости от сезонной освещенности/

В 1840 году Большая Западная железная дорога ввела Гринвичское время (GMT). 

Ливерпуль и Манчестер поддержали начинание в 1846 году. 

С распространением телеграфа Королевская обсерватория в Гринвиче смогла передавать сигналы точного времени по всей стране почти мгновенно, что позволяло городам синхронизировать часы. 

Тем не менее колокола Башни Тома – колокольни Крайст-чёрч, одного из крупнейших колледжей Оксфорда, до сих пор звонят через пять минут после наступления каждого часа.

18 ноября 1883 года получил имя День двух полудней;

в этот день станционные часы по всему континенту были переустановлены. 

США разделили на пять часовых поясов: 

атлантический (межколониальный), восточный, центральный, горный и тихоокеанский.

в 1884 годe на Международной меридианной конференции предложили разбить всю Землю на 24 часовых пояса, создав единое стандартное время. 

Земной шар был разделен на 24 воображаемые линии, известные как меридианы, идущие с Южного полюса к Северному. 

Стандартный день начинается в полночь на нулевом меридиане Гринвича. 

К 1900 году почти все районы Земли входили в один из стандартных часовых поясов.

18 апреля 1961 года  Кеннеди издал приказ нанести удар по позициям кубинской армии самолетами В26, базирующиеся в Никарагуа. 

Бомбардировщики должны были прикрывать реактивные самолеты с американского авианосца «Уэссекс». 

Воздушный удар был запланирован на 06:30 утра 19 апреля.

К назначенному времени истребители прикрытия вышли в район встречи с бомбардировщиками – но тех там не было. 

Летчики В26, жившие по центральному никарагуанскому времени, прибыли на целый час позже, в 7:30 по кубинскому восточному времени. 

Без прикрытия давно ушедших истребителей В26 оказались беззащитны – ВВС Кастро смогли сбить два B26 с американской символикой, что неопровержимо доказывало причастность США к попытке переворота. 

Политические последствия простой путаницы с часовым поясом были огромны – Куба прочно вошла в социалистическую систему, а год спустя разразился Карибский кризис.

многие считают, что наличие большего количества делителей –

 шесть (1, 2, 3, 4, 6 и 12) 

против четырех (1, 2, 5 и 10) 

– дает двенадцатеричной системе преимущество перед десятеричной.

Сторонники двенадцатеричной системы утверждают, что она уменьшает необходимость округления и, следовательно, решает ряд общих проблем. 

в прошлом многие из бурно развивающихся индустриальных стран широко использовали имперские метрические системы, основой которых было число 12. 

В футе 12 дюймов, а в дюйме – 12 линий. 

Первоначально и в имперском (британском) фунте было 12 унций. 

Слово «унция» происходит от того же самого латинского слова, что и дюйм – uncia, означавшего одну двенадцатую часть. 

имперская тройская система, которая используется для измерения массы драгоценных металлов и драгоценных камней, до сих пор делит тройский фунт на 12 тройских унций. 

Старый британский денежный фунт состоял из 20 шиллингов, каждый из которых состоял из 12 пенсов. 

Это означало, что 240-пенсовый фунт можно было разделить нацело двадцатью разными способами.

Сегодня США – в компании Либерии и Мьянмы – остаются единственными странами мира, где метрическая система широко не используется; 

Мьянма, правда, пытается покинуть это трио и перейти на метрическую систему. 

Американский нонконформизм в этом вопросе зиждется на скептицизме и упрямом традиционализме многих граждан этой страны. 

(Бинарное мышление).

Чаще всего быстрое (и сверхосторожное) бинарное решение лучше, чем неторопливое, взвешенное, просчитывающее все варианты. 

Эта бинарная манера принятия решений не менялась в своей основе даже с развитием и усложнением общественных отношений. 

Мы продолжали опираться на стереотипные представления о наших ближних – считали их хорошими или плохими, святыми или грешниками, друзьями или врагами. 

Мы обманываемся, выбирая между черным и белым, тогда как на самом деле в спектре гораздо больше цветов.

«препарируя» прошлые ошибки, современные математические технологии предоставляют нам способы избежать таких просчетов в будущем – иногда, правда, эффективность этих способов сомнительна.

(Глава 6. Бесконечная оптимизация: безграничный потенциал алгоритмов – от эволюции до электронной коммерции).

В топологии фактические формы самих объектов неважны, 

объекты группируются по количеству отверстий, которыми они обладают. 

Бублик, имеющий одно отверстие, принципиально более сложная фигура, чем футбольный мяч, который отверстий не имеет. 

В 2002 году российский математик-отшельник Григорий Перельман поделился с сообществом топологов тремя сложными для понимания математическими статьями. 

Эти работы предполагали решение проблемы в четырех измерениях. 

Несколько групп математиков потратили три года, чтобы удостовериться в верности его доказательств. 

В 2006 году, в год, когда Перельману исполнилось 40 лет – предельный возраст для получения премии, – он был награжден медалью Филдса, математическим эквивалентом Нобелевской премии. 

но настоящей сенсацией стал отказ Перельмана от почестей. 

Он оказался первым человеком, отказавшимся от медали Филдса. 

В своем заявлении об отказе Перельман сказал: 

«Меня не интересуют ни деньги, ни слава. 

Я не хочу, чтобы меня выставляли напоказ, как животное в зоопарке». 

В 2010 году Математический институт Клэя наконец признал, что Перельман все же заслужил 1 миллион долларов за решение одной из «Проблем тысячелетия», но питерский математик отказался от их денег.

Работа Перельмана, несомненно, чрезвычайно важна в области чистой математики, но применить доказательство гипотезы Пуанкаре на практике шансов немного. 

То же самое относится и к большинству других «Проблем тысячелетия». 

Однако доказательство или опровержение гипотезы номер семь – известной в математическом сообществе под кратким и несколько загадочным названием P vs NP,

а в российском математическом сообществе еще и как проблема перебора 

– может иметь широкомасштабные практические последствия в таких разнообразных областях, как интернет-безопасность и биотехнология.

В основе проблемы P vs NP лежит идея, что проверить правильность решения задачи зачастую проще и быстрее, чем собственно решение найти. 

Этот важнейший из открытых математических вопросов сводится к следующему: 

если положительный ответ на какой-то вопрос можно довольно быстро проверить при помощи компьютера, верно ли, что ответ на этот вопрос можно довольно быстро найти?

Чтобы провести аналогию, представьте, что вы собираете пазл из однообразного изображения, вроде картинки чистого голубого неба. 

Перепробовать все возможные комбинации кусочков, чтобы понять, подходят ли они друг другу, – трудная задача. 

Однако, как только пазл закончен, правильность его сборки проверить легко.

Более строгие определения эффективности математические выражаются в описании того, насколько быстро работает алгоритм по мере усложнения проблемы – когда к пазлу добавляется больше кусочков. 

Набор задач, которые можно решить быстро (в так называемом полиномиальном времени), называется классом сложности P. 

Бóльшая группа задач, которые можно быстро проверить, но не обязательно можно быстро решить, называется классом сложности NP (что расшифровывается как недетерминированное полиномиальное время). 

Задачи типа P – это подмножество задач типа NP, так как, решив задачу быстро, мы автоматически проверяем найденное решение.

А теперь представьте, что нужно построить алгоритм собирания любого пазла.

если алгоритм входит в группу NP, то с увеличением количества кусочков время, затрачиваемое на его решение, может вырасти по экспоненте. 

В сущности, литерой «P» можно было бы обозначать проблемы, решаемые на практике, а литерами «NP» – Не Решаемые на практике.

Проблема «P vs NP» заключается в вопросе, все ли проблемы класса NP, решения которых можно быстро проверить, но алгоритм быстрого решения, которых неизвестен, действительно являются и членами класса P. 

Может быть, проблемы класса NP имеют практический алгоритм решения, но мы его просто еще не нашли? 

В математической терминологии, равны ли P и NP? 

Если да, то, как мы увидим, потенциал применения этого равенства – даже для решения повседневных задач – огромен.

Самый простой алгоритм сортировки называется пузырьковая сортировка (или сортировка простыми обменами). 

В 2008 году, Эрик Шмидт, генеральный директор Google,

в шутку сказал кандидату в президенты Бараку Обаме, что баллотироваться на пост президента – примерно то же самое, что и проходить собеседование при приеме на работу в Google. 

А затем задал ему один из вопросов, которые задают на таком собеседовании:

 

«Как вы определите хорошие способы сортировки одного миллиона 32-битных целых чисел в двух мегабайтах оперативной памяти?» 

Чувствуя растерянность Обамы, Шмидт попытался вмешаться, 

но Обама сказал: 

«…нет-нет-нет, я думаю, что делать это через “пузырьки” – не лучшая идея», 

Раздался гром аплодисментов и одобрительные крики собравшихся компьютерщиков. 

Неожиданная эрудиция Обамы основывается на шутке «для посвященных» о неэффективности пузырькового алгоритма сортировки.

В задаче коммивояжера, с ростом количества пунктов доставки сложность выбора оптимального маршрута растет лавинообразно – происходит так называемый комбинаторный взрыв. 

Вариативность маршрута с добавлением к нему новых локаций растет быстрее экспоненты.

Подавляющее большинство математиков считают, что P и NP – это принципиально разные классы проблем и что у нас никогда не будет быстрых алгоритмов для коммивояжеров или маршрутизации транспортных средств. 

Возможно, это к лучшему. 

Задача принятия решения с бинарным вариантом ответа для проблемы коммивояжера – канонический пример подгруппы задач, известной как NP-полные.

Поскольку почти вся криптография в интернете полагается на сложность решения определенных NP задач, доказательство того, что P равно NP, может быть губительным для онлайн-безопасности.

С другой стороны, тогда мы могли бы разработать быстрые алгоритмы для решения всевозможных логистических задач. 

Фабрики могли бы организовать производственный процесс с максимальной эффективностью, 

а службы доставки находили бы самые эффективные маршруты транспортировки, что потенциально снижало бы цену товара – даже если его больше нельзя было бы безопасно заказать онлайн! 

По сути своей, проблема P vs NP – это очень непростая попытка выяснить, можно ли автоматизировать человеческое творчество.
(Жадные алгоритмы).
Мы можем использовать эвристические алгоритмы (упрощения, основанные на здравом смысле, или эмпирические правила), которые призваны приблизить нас к оптимальному решению для широкого круга типологически близких задач.

Одно из семейств таких алгоритмов называется жадными алгоритмами. 

Эти краткосрочные процедуры нацелены на поиск лучшего локального выбора в попытке найти глобально оптимальные решения.

Представьте, что вы впервые оказались в какой-то местности и хотите подняться на самый высокий холм, чтобы осмотреться. 

Жадный алгоритм подъема на вершину сводится к тому, чтобы сначала найти самый крутой уклон по отношению к вашей текущей позиции, а затем сделать шаг в этом направлении. 

На каждом шаге эта процедура повторяется до тех пор, пока вы не окажетесь в точке, по всем направлениям от которой будут лишь скаты. 

Это означает, что вы достигли вершины холма – но не обязательно самого высокого холма вокруг. 

Жадный алгоритм не гарантирует, что вы подниметесь на самую высокую вершину. 

Возможно, что маршрут к вершине небольшого холма, на который вы только что взобрались, просто начинался круче, чем тот, который привел бы вас к вершине местного горного хребта, а выбор ошибочного маршрута был продиктован вашей эвристической близорукостью. 

Жадные алгоритмы могут найти решения, но не всегда гарантированно лучшие.

Однако для проблем определенного типа жадные алгоритмы оптимальны.

Жадные алгоритмы – когда они работают – предлагают высокоэффективные методы решения проблем. 

Однако когда они не работают, они оказываются вредны. 

Намереваясь отправиться на лоно природы и взобраться на самую высокую вершину, чтобы подышать свежим горным воздухом, очутиться на верхушке кротовой кучи на своем заднем дворе из-за того, что вы воспользовались негибким жадным алгоритмом, будет не очень-то приятно. 

Такой результат оптимальным не назовешь. 

К счастью, существует ряд алгоритмов, вдохновленных самой природой, которые помогают нам преодолевать как образные, так и настоящие препоны.

Одна из процедур, известная как муравьиный алгоритм, посылает армии компьютерных «муравьев» для исследования виртуальной среды, отражающей реальную проблему. 

Так, при решении задачи коммивояжера муравьи снуют между близлежащими пунктами назначения, отражая способность настоящих муравьев воспринимать лишь ближайшее для них окружение. 

Если муравьи находят короткий маршрут по всем точкам, то они метят его феромонами, чтобы направить по нему других муравьев. 

Более востребованные и, соответственно, более короткие маршруты привлекают больше муравьиного трафика.

выделенный феромон испаряется, позволяя муравьям гибко менять оптимальную маршрутизацию при изменении пунктов назначения. 

Муравьиный алгоритм используется для поиска эффективных решений проблем NP-группы – таких как проблема маршрутизации транспортных потоков, – а также для моделирования сложнейших биологических процессов, включая особенности формирования многокомпонентных трехмерных белковых структур из простых одномерных цепочек аминокислот.

Муравьиный алгоритм – всего лишь один из целого семейства так называемых алгоритмов роевого интеллекта, вдохновленных природой.

Стаи скворцов или косяки рыб способны очень резко – и при этом согласованно и синхронно – менять направление движения, несмотря на то что каждая особь может коммуницировать лишь с небольшим числом особей по соседству. 

Информация о появлении хищника неподалеку от одного края косяка рыбы, например, быстро распространяется на другой его край. 

Заимствуя эти принципы локального взаимодействия, разработчики алгоритмов могут использовать огромные «стаи» исполнительных устройств, объединенных в информационную сеть, для исследования окружающей среды. 

Их быстрое, «роевое» взаимодействие позволяет им узнавать об открытиях, сделанных другими участниками «роя» в поисках оптимального окружения.

Самый известный природный алгоритм – эволюция. 

Для создания биоразнообразия, способного решить некоторые из самых сложных проблем планеты, достаточно исполнять всего лишь три простые процедуры – отбирать, комбинировать и мутировать.

Однако слепой ход эволюции, которая просто перебирает имеющиеся возможности, не следует путать с целенаправленным поиском совершенства. 

Эволюция, как правило, находит решение, которое подходит больше, чем любое предыдущее решение для этой среды, но не всегда лучшее.

ученые-компьютерщики многократно заимствовали ключевые постулаты наиболее известного из естественных алгоритмов – прежде всего, в виде так называемых генетических алгоритмов. 

Эти инструменты используются для решения задач планирования и для поиска хороших, если не идеальных, решений сложных задач класса NP – таких, как задача о рюкзаке.

Задача о рюкзаке – это история торговца, который хочет унести с собой на рынок как можно больше товаров в рюкзаке с ограниченной вместимостью.

Наилучшее решение проблемы рюкзака – отобрать товары, которые принесут самый большой доход. 

Вариации задачи о рюкзаке возникают при необходимости вырезать фигурные формы из теста или при попытке сэкономить на оберточной бумаге, упаковывая подарки. 

Та же проблема возникает при погрузке судов и фур. 

Когда диспетчер загрузки определяет, какие куски данных нужно загрузить и в каком порядке, чтобы максимально использовать ограниченную пропускную способность интернет-канала, он пытается решить задачу о рюкзаке.

Генетический алгоритм начинается с генерации заданного числа потенциальных решений проблемы. 

Эти решения являются родительским поколением. 

Для задачи о рюкзаке это родительское поколение создает списки пакетов – наборы предметов, которые могут поместиться в рюкзак. 

Алгоритм ранжирует решения по тому, насколько хорошо они решают проблему. 

В задаче о рюкзаке критерием ранжирования становится прибыль, которую может принести каждый набор предметов, помещающийся в рюкзак. 

Затем выбираются два лучших решения – наборы, приносящие наибольшую прибыль. 

Некоторые наборы из одного хорошего решения отбрасываются, а остальные комбинируются с некоторыми наборами из другого хорошего решения.

Как только в новом поколении создано первое дочернее решение, выбираются еще два наиболее эффективных родительских, которые будут воспроизводиться. 

Таким образом, лучшие решения в родительском поколении передают свои характеристики бóльшему количеству дочерних решений в следующем поколении. 

Этот комбинированный процесс повторяется до тех пор, пока не возникнет достаточно «дочек», чтобы заменить все оригинальные решения в родительском поколении. 

Сделавшие свое дело родительские решения уничтожаются, а дочерние переходят в статус родительских и весь цикл «отбор – комбинация – мутация» начинается заново.

Дочерним решениям присущ случайный характер, поэтому алгоритм не гарантирует, что все «дочки» будут лучше своих «родителей». 

выбирая, какие из дочерних решений станут воспроизводиться – это можно назвать виртуальным дарвинизмом, – алгоритм отбрасывает неполноценные решения и позволяет передать свои характеристики следующему поколению только лучшим. 

Как и в случае с другими алгоритмами оптимизации, в результате мы можем получить локальный оптимум, любое изменение которого приведет к снижению качества, но не достичь наилучшего из возможных решений.

Случайность, являющаяся столь важной особенностью генетических алгоритмов, играет определенную роль и в нашей повседневной жизни. 

Плагины Netflix предлагают вам случайные фильмы или сериалы, исходя из ваших предыдущих предпочтений.

Стратегия оптимальной остановки задается вопросом, сколько ресторанов нужно посмотреть и отклонить, чтобы получить представление о том, какой у вас выбор? 

Если посетите слишком мало ресторанов, вы не поймете, что предлагается к рассмотрению, но если вы исключите из списка слишком много, оставшийся выбор будет ограничен.

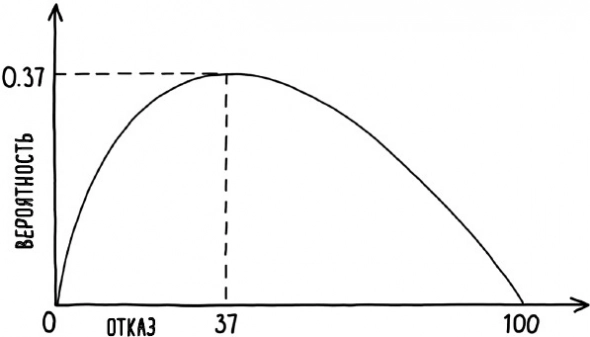
(Рис. 21. Оптимальная стратегия)

Оптимальная стратегия заключается в том, чтобы оценить, но отклонить каждый вариант до заданной точки отсечения, а затем принять следующий оцениваемый вариант, который лучше всех предыдущих.

оказывается, что следует оценить и отвергнуть примерно первые 37 % ресторанов, прежде чем выбрать следующий, который лучше всех предыдущих. 

Точнее, нужно отвергнуть 1/e долю всех доступных вариантов, где e – математическое обозначение числа Эйлера. 

Число Эйлера составляет приблизительно 2,718, таким образом, 1/e – 37 %. 

 если вы выбираете слишком долго, то, скорее всего, вы уже пропустили лучший вариант. 

Вероятность наилучшего выбора максимальна, когда вы отклоняете первые 37% вариантов.

(Рис. 22)

Но что, если лучший ресторан был в первых 37 %? 

:--) В таком случае, вам не повезло. 

Правило 37 % работает не каждый раз – оно вероятностное. 

Стратегия оптимальной остановки работает не только для ресторанов. 

изначально математики окрестили ее «проблемой найма».

Проведите собеседование с 37 % кандидатов и используйте их в качестве ориентира. 

Возьмите после этого первого кандидата, который окажется лучше всех тех, кого вы видели до него, и откажите остальным.

Существуют даже алгоритмы оптимальной остановки, которые подскажут, сколько кавалеров (или пассий) вам нужно перебрать, прежде чем задумываться о браке. 

Сначала нужно решить, сколько увлечений вы захотите пережить к тому времени, когда пожелаете остепениться.

 Допустим, вы остановитесь на одном романе в год с 18 по 35 лет, что составит в общей сложности 17 потенциальных партнеров на выбор. 

Стратегия оптимальной остановки предполагает, что вы играете на этом поле около шести или семи лет (примерно 37 % от 17 лет), определяясь с выбором. 

После этого вы должны остаться с первым же человеком, который вам подойдет лучше всех тех, с кем вы встречались до того.

:--) Идея подчинить свою романтическую жизнь заданному набору правил придется по душе немногим. 

Что, если в первых 37 % вы найдете того, с кем по-настоящему счастливы? 

Можете ли вы действительно хладнокровно отвергнуть свои чувства, следуя любовной миссии по алгоритму? 

Что, если человек, которого алгоритм определил вам в спутники жизни, вовсе не считает вас наилучшей парой для себя? 

Что, если ваши приоритеты изменятся на полдороге? 

К счастью, в сердечных вопросах, как и в других, более очевидных математических проблемах оптимизации, нам не всегда нужно искать лучшее решение, тот единственный и неповторимый Идеал.

Скорее всего, есть несколько человек, которые будут вам хорошей парой и с которыми вы сможете быть счастливы. 

Оптимальная остановка не дает ответов на все вопросы в жизни.

В 1939 году Министерство информации Великобритании разработало три плаката.

Третий плакат, напечатанный, был отложен на время – его собирались использовать в случае ожидавшихся жестоких и потенциально деморализующих массовых авианалетов и бомбардировок. 

Но в сентябре 1940 года, из-за нехватки бумаги и очевидного пафосного высокомерия первых двух плакатов всю наглядную агитацию отправили в переработку. 

Третий плакат за пределами Министерства информации не видел почти никто.

потерянный плакат Министерства информации обнаружили только в 2000 году: 

Он гласил «Сохраняйте спокойствие и продолжайте действовать»

Keep-calm-and-carry-on.

в 2008 году этот мем взорвал сознание мирового сообщества.

Рецессия охватывала мир, и многие стремились пробудить в себе непреклонность и твердость духа. 

«Сохраняйте спокойствие и продолжайте действовать» – это было в точку.

(рис. 22.1 Keep-calm-and-carry-on)

Лозунг заимствовали самые разные рекламные кампании – от индийских ресторанов («Сохраняйте спокойствие и добавьте карри»)

 до презервативов («Сохраняйте спокойствие и надевайте его»).

ассортимент компании, продающей футболки с такими принтами, насчитывал около 1000 различных позиций. 

Владелец компании перешел на печать по требованию. 

Это позволяло ему значительно разнообразить свое предложение, печатая при этом только заказанные принты. 

Наладив процесс печати, он занялся написанием компьютерных программ, которые автоматически генерировали эскизы. 

Ассортимент вырос до более чем десяти миллионов позиций. 

алгоритм работал со списками глаголов и существительных, объединяя их по простой формуле 

«Сохраняйте спокойствие и [глагол] [существительное]». 

Фразы, сгенерированные программой, накладывались на изображение футболки и выставлялись на продажу на Amazon.

автоматически выставились на продажу несколько футболок с фразами типа «Сохраняйте спокойствие и пните ее» 

или «Сохраняйте спокойствие и насилуйте всех».

Алгоритм, казавшийся в свое время замечательной идеей, в итоге привел компанию к банкротству.