20 декабря 2020, 12:31
Физико-математические основы Грааля. Часть 2
При обсуждении основ построения граальной ТС, у страждущих возникли философские вопросы:
1. а где математика, где вожделенные формулы?
2. а зачем нужно распределение Эрланга для интервалов времени между котировками? Мы-де привыкли все делать, используя OHLC, и Грааль и так уже давно у нас в руках.
Постараюсь ответить на эти вопросы.
1. Вся математика с вожделенными формулами описана в теории диффузионных случайных процессов. Могу порекомендовать следующую литературу:
Гардинер К.В. «Стохастические методы в естественных науках»
Попов П.В. «Диффузия»
применительно к финансам:
Rama Cont, Peter Tonkov «Financial Modelling with jump processes»
Фактически, все сводится к анализу уравнений Ланжевена или Фоккера-Планка для движения диффундирующей частицы.
Для практических целей, необходимо изучить вид распределения приращений протекающего процесса и воспользоваться формулами конкретной подходящей модели.
К примеру, вид распределения приращений цены на рынке подобен распределению приращений для Variance Gamma Process:
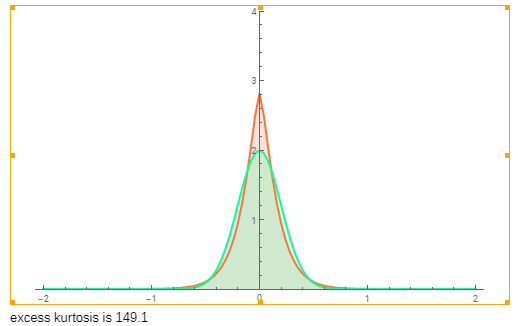
Посмотреть можно здесь:
https://demonstrations.wolfram.com/TheReturnDistributionOfTheVarianceGammaProcess/
Прекрасно.
Этот процесс записывается в виде
(1)
и имеет следующие центральные моменты
![E[X(t)] = \theta t](https://wikimedia.org/api/rest_v1/media/math/render/svg/87663f79ebb161f3a396db2e3046a79d8b91196e "Физико-математические основы Грааля. Часть 2")
![Var[X(t)] = (\theta^2 \nu + \sigma^2)t](https://wikimedia.org/api/rest_v1/media/math/render/svg/78689e11d9fde98104a50b983cf003c007bf64ab "Физико-математические основы Грааля. Часть 2")
Этот процесс имеет свойство «возврата к среднему» (mean reversion process) как и процесс Орнштейна-Уленбека для гауссовских приращений.
Т.о. стратегия ТС, основанная на применимости Variance Gamma Process к рынку, должна быть построена на возврате цены с среднему значению после ее выхода за пределы дисперсионного канала.
Корректно или нет определение среднего как
(2)
именно к рыночному процессу — вопрос открытый, т.к. задает простое смещение (дрейф) протекающего марковского процесса, а на рынке необходим учет немарковости, но это отдельная обширная тема для разговора...
2. Итак, понятно, что цена, в первом приближении, имеет свойство возврата к среднему, после ее выхода за пределы дисперсионного канала, определяемого вторым центральным моментом
(3)
Но, на рынке, как обычно, все не так просто....
Время t здесь принципиально нелинейно и воспользоваться этой формулой напрямую мы не можем. Необходимо учитывать поправки, вносимые этой нелинейностью.
Изучая природу протекающего процесса, можно прийти к выводу, что поток событий (приход новых тиковых котировок) удовлетворяет некоему процессу Пальма для каждого конкретного поставщика. Вывести формулы под конкретный процесс достаточно трудоемко. Поэтому, необходимо свести процесс к известному процессу Эрланга.
Получив вожделенный поток Эрланга с определенным порядком k и интенсивностью lambda=tau/t, где tau — количество котировок, пришедших за время t, необходимо использовать среднее значение времени протекающего процесса Mean(t)=k/lambda=(k*t)/tau.
Подставляя полученное выражение в формулу (3), получим уточненную формулу для дисперсии процесса в нелинейном времени, принадлежащего к распределению Эрланга.
М-да.....
Продолжение, наверное, следует...
Toddler.
1. а где математика, где вожделенные формулы?
2. а зачем нужно распределение Эрланга для интервалов времени между котировками? Мы-де привыкли все делать, используя OHLC, и Грааль и так уже давно у нас в руках.
Постараюсь ответить на эти вопросы.
1. Вся математика с вожделенными формулами описана в теории диффузионных случайных процессов. Могу порекомендовать следующую литературу:
Гардинер К.В. «Стохастические методы в естественных науках»
Попов П.В. «Диффузия»
применительно к финансам:
Rama Cont, Peter Tonkov «Financial Modelling with jump processes»
Фактически, все сводится к анализу уравнений Ланжевена или Фоккера-Планка для движения диффундирующей частицы.
Для практических целей, необходимо изучить вид распределения приращений протекающего процесса и воспользоваться формулами конкретной подходящей модели.
К примеру, вид распределения приращений цены на рынке подобен распределению приращений для Variance Gamma Process:
Посмотреть можно здесь:
https://demonstrations.wolfram.com/TheReturnDistributionOfTheVarianceGammaProcess/
Прекрасно.
Этот процесс записывается в виде
(1)и имеет следующие центральные моменты
The mean of a variance gamma process is independent of 
The variance is given as
Этот процесс имеет свойство «возврата к среднему» (mean reversion process) как и процесс Орнштейна-Уленбека для гауссовских приращений.
Т.о. стратегия ТС, основанная на применимости Variance Gamma Process к рынку, должна быть построена на возврате цены с среднему значению после ее выхода за пределы дисперсионного канала.
Корректно или нет определение среднего как
(2)именно к рыночному процессу — вопрос открытый, т.к. задает простое смещение (дрейф) протекающего марковского процесса, а на рынке необходим учет немарковости, но это отдельная обширная тема для разговора...
2. Итак, понятно, что цена, в первом приближении, имеет свойство возврата к среднему, после ее выхода за пределы дисперсионного канала, определяемого вторым центральным моментом
(3)Но, на рынке, как обычно, все не так просто....
Время t здесь принципиально нелинейно и воспользоваться этой формулой напрямую мы не можем. Необходимо учитывать поправки, вносимые этой нелинейностью.
Изучая природу протекающего процесса, можно прийти к выводу, что поток событий (приход новых тиковых котировок) удовлетворяет некоему процессу Пальма для каждого конкретного поставщика. Вывести формулы под конкретный процесс достаточно трудоемко. Поэтому, необходимо свести процесс к известному процессу Эрланга.
Получив вожделенный поток Эрланга с определенным порядком k и интенсивностью lambda=tau/t, где tau — количество котировок, пришедших за время t, необходимо использовать среднее значение времени протекающего процесса Mean(t)=k/lambda=(k*t)/tau.
Подставляя полученное выражение в формулу (3), получим уточненную формулу для дисперсии процесса в нелинейном времени, принадлежащего к распределению Эрланга.
М-да.....
Продолжение, наверное, следует...
Toddler.
22:10
Advocate, и какой ништяк — ей вынес «самый гуманный» суд в Мире?
— Явно несоизмеримо малый — содеянному(учел наличие малолетних детей на иждевении)!
Дмитрий Соколов,… просто!
Пруфы для чего?
Oyy, да в принципе он всегда так ходит, редко когда прям точно совпадает
• Производство стали 11м 2024г: МИР 1,695 млрд т (-1,4% г/г), Ноябрь 146,8 млн т (+0,8% г/г).
• 11м 2024г: Китай 929,2 млн т (-2,7% гг), Ноябрь 78,4 млн т (+2,5% г/г).
• 11м 2024г: Индия 135,9 мл...
• Производство стали 11м 2024г: МИР 1,695 млрд т (-1,4% г/г), Ноябрь 146,8 млн т (+0,8% г/г).
• 11м 2024г: Китай 929,2 млн т (-2,7% гг), Ноябрь 78,4 млн т (+2,5% г/г).
• 11м 2024г: Индия 135,9 мл...
• Производство стали 11м 2024г: МИР 1,695 млрд т (-1,4% г/г), Ноябрь 146,8 млн т (+0,8% г/г).
• 11м 2024г: Китай 929,2 млн т (-2,7% гг), Ноябрь 78,4 млн т (+2,5% г/г).
• 11м 2024г: Индия 135,9 мл...
Виталий Б., блин, уже даже не слежу за новостями)) а где это сообщение?
21:41
Nikstudent, в точку! нефть скоро будет по 40, а следом и лукойл по 4000
21:41
• Производство стали 11м 2024г: МИР 1,695 млрд т (-1,4% г/г), Ноябрь 146,8 млн т (+0,8% г/г).
• 11м 2024г: Китай 929,2 млн т (-2,7% гг), Ноябрь 78,4 млн т (+2,5% г/г).
• 11м 2024г: Индия 135,9 мл...
Вообще для грааля нужна триада — прогер+трейдер+математик.
В идеале это один чел, но может быть и три, если друг друга слышат.
Этот пост плюсанул за то, что них не понял )))
Теперь я понял почему мы с вами во многом совпадаем.
Колдун тоже физик?
А говоря о математиках, я имел ввиду владение матаппаратом.
Если часть ценовых рядов имеет более-менее выраженную персистентность, как это укладывается в антиперсистентность Вашей идеальной модели.
Почему Вы вообще решили, что она подходит для всех ценовых рынков. Нас учили во времена торжествующего Учения, что критерий истины — практика. У Вас есть практическое доказательство необходимости использовать именно такой математический инструментарий?
1. Объяснение «тяжёлых хвостов» приращений цен через дифференциальные уравнения в частных производных далеко не единственно.
2. В рамках любой модели ценообразования надо ещё, как минимум, объяснить и нестационарность процесса квадратов приращений цен. Эрланг в этом вопросе не слишком подходящ.
Проблема «тяжелых хвостов» и нестационарности процесса, действительно, существует.
Поэтому, выбранная модель, в частности Variance Gamma Process, должна максимально их решать.
Напрямую, она, конечно, их не решает. Поэтому, мне пришлось работать над ее усовершенствованием. Прореживание по Эрлангу тикового ряда дает такую возможность.
Физико-математические основы Грааля:
понижать ставки
конец
Цены, по мнению автора, имеют тенденцию возврата к среднему. Проводим среднюю линию и относительно нее смотрим распределение. Внизу покупаем — вверху продаем. Обычный канал, и ничего более. Все.
Остальное — математические экзерсисы автора. Главное, чтобы ему самому нравилось. Остальное неважно.
есть 2 варианта
1 на пробой боллинджера — торгуем тренд — и все ок...
2 отбой от боллинджера — торгуем контртренд… и не работает из-за хвостов
вообще как только афтор перейдет от модели к тестам… особенно к стрес тестам на 2008г… все будет ясно и понятно
Тестов у тоддлера нет, он, насколько помню, больше с тиками общается.
На рынке немного другой процесс — гамма. И даже еще сложнее. Но, суть проста — это некий снос (дрифт) + некий интегрированный (не белый!) шум вокруг сноса с определенными границами. Если процесс принадлежит к классу mean reversion, то и отлично.
Собственно, в мою задачу не входит подробное описание своей ТС. Зачем мне это? Я лишь показываю возможные направления исследований для страждущих. А выбирать или нет сей путь — воля каждого. Пусть думают, выбирают, изучают. Так велел Колдун.
Типичные ошибки физика, применяющего законы Вселенной к процессам в Воздушном Шарике. Емкость Рынка не стремится к бесконечности, а посему воздействия не уравновешиваются в любые промежутки времени.