18 июня 2019, 23:46
Дельта-хеджирование при изменяющейся волатильности
В прошлой статье, про механизм работы дельта-хеджирования, уважаемые Дмитрий Новиков и ch5oh, оставили весьма полезные комментарии, спасибо им за это! Это натолкнуло меня на мысль, смоделировать поведение ДХ при изменяющейся волатильности и посмотреть, что из этого выйдет.
Здесь не будет никакой теории, просто несколько графиков. Эта статья скорее как дополнение к предыдущей, чтобы подвести итог о прибыли.
(Для каждого эксперимента произведено 1000 генераций поведения БА, с указанной волатильностью.)
Поведение ДХ, когда волатильность не меняется:
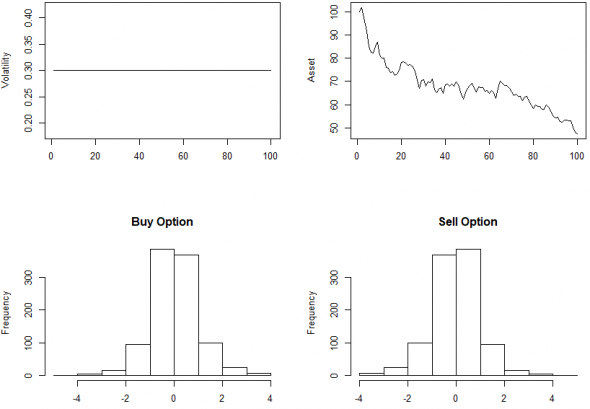
Всё около нуля как и должно быть.
Поведение ДХ, когда волатильность растет:
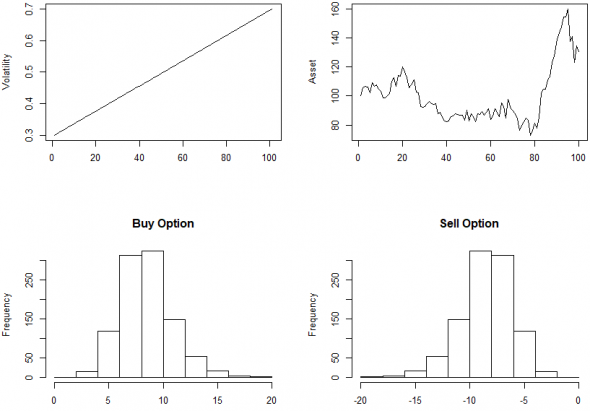
Поведение ДХ, когда волатильность снижается:
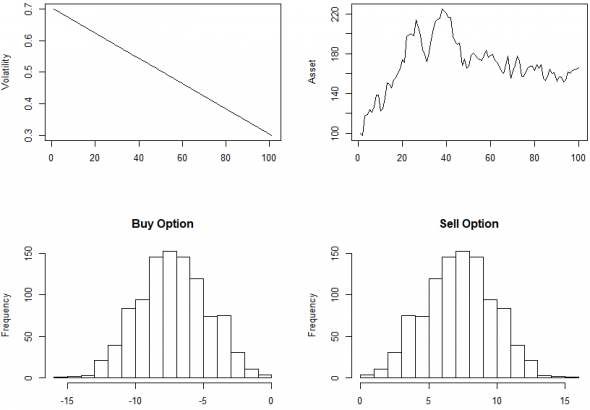
Теперь становится понятней, откуда берется прибыль.
В будущем попробуем смоделировать волатильность волатильности и посмотреть, что с этим можно сделать.
Код: https://github.com/dmitryy/finance/blob/master/RScripts/delta-hedge-volatility.R
Здесь не будет никакой теории, просто несколько графиков. Эта статья скорее как дополнение к предыдущей, чтобы подвести итог о прибыли.
(Для каждого эксперимента произведено 1000 генераций поведения БА, с указанной волатильностью.)
Поведение ДХ, когда волатильность не меняется:
Всё около нуля как и должно быть.
Поведение ДХ, когда волатильность растет:
Поведение ДХ, когда волатильность снижается:
Теперь становится понятней, откуда берется прибыль.
В будущем попробуем смоделировать волатильность волатильности и посмотреть, что с этим можно сделать.
Код: https://github.com/dmitryy/finance/blob/master/RScripts/delta-hedge-volatility.R
genubat, Источник сообщает, что — с ноября 2023г., американцы потеряли над Йеменом 3
БПЛА MQ-9.
По-минимуму: 20х200.
по-человечески: 35Х250.
По-максимуму; 51Х510.
по-свинообезъяньи: сами знаете.
1:33
кто разогнал этоо кал?
AndreyСт, мне — не только от Сбера, мне и от Альфы ничего не было
a_tak, ну… это был Я.Кроме шуток = МНОГО других Организаций)))
ВСЕ — заинтересованы в росте капы. Просто Банки.И переподписка была не просто так. Ворон-ворону...
Tonikvzakone, не на 6к
333V, в прошлый раз 15 давали
0:01
Георгий Х., или наоборот перед большими праздниками скинуть не уверенных
Tonikvzakone, с учётом виндфола остаётся по моим расчетам около 81 рубля из расчета 50% нераспределенки скорр. ЧП за 2023. Может попозже и выплатят бонусом, когда кеш появится (может уже появился?)...
Чингачгук (Великий Змей), я не про тебя
Dmitryy, если задача состот в том, чтобы развлечься, а не заработать — не вопрос.
=) "Нет преград для патриотов!" © ДМБ
Многие с первых шагов рвутся в бой и сливают. Я не хочу искать свои грабли, я хочу сначала изучить поле граблей, а потом аккуратно идти к цели :)
Dmitryy, опционное поле можно изучать бесконечно. И граблей там намного больше, чем можно ожидать, учитывая количество толстых серьезных книжек по теме.![]()
Будет примерно то же, что и при неизменной.
Лог-нормальное распределение в логарифмическом масштабе должно получиться) А оно близко к Гауссу Блэка-Шоулза.
Осталось понять, какая у неё автокорреляция) МОЖ и так хорошо известно по HV.
В первом случае сигмы одинаковые, левый верхний график прямая линия. И результат благодаря ДХ около нуля, тут по теории всё верно.
Далее, сигма либо линейно растет, либо линейно снижается, актив моделируется тоже по этой же меняющейся сигме, т.е. Sn по сигме(n), а Sn+1 по сигме(n+1). Возможно ошибка в модуляции актива?
И в N(d1), соответственно тоже передается постоянно меняющаяся сигма. На выходе получаем доходность или убыток.
Т.е. да, это не противоречит вашему выводу, разница получилась из-за меняющейся сигмы.
Смотря для какого случая:
1. 0.3
2. 0.3 -> 0.7 (равномерно растет за 100 шагов)
3. 0.7 -> 0.3 (равномерно падает за 100 шагов)
Я не акцентировал тут внимание на правильном моделировании волы, тут я скорее хотел понять как меняется прибыль от направления волы. Я понимаю, что волу надо моделировать по другому, но это будет потом.
df/dt*(t-t0)+df/dS*(S-S0)+0,5*ddf/dS^2*(S-S0)^2+df/dsigma*(sigma-sigma0)+...=r*f
следует, что изменение волатильности при ДХ и r=0 создаёт направленную позицию в портфеле, т.е. sigma-sigma0=-(df/dS)/(df/dsigma)*(S-S0)+...
Вся сложность ещё и в производных по волатильности.
пс: sigma и sigma0 — HV или IV (без разницы)
Это как я на данный момент понимаю, и есть точка извлечение прибыли?