О вычислении дельты опциона

Дискуссии о правильных и неправильных методах вычисления дельты опциона. Дошел до темы «Липкая денежность» против «липкого страйка».

Больше всего смущает то, что в работе Блэка и Шолеса, на которую постоянно ссылаются оппоненты, нет вообще никаких упоминаний о «кривой волатильности», волатильность у БШ есть константа. Чем «кривее» кривая IV для конкретного рынка, тем меньше модель БШ подходит для его описания, это вся информация, которую кривая IV в себе содержит.

Спор о том, следует ли учитывать ее наклон при вычислении дельты, подобен спору о количестве чертей, способных уместиться на острие иголки. Мне кажется, правильнее изменить модель БШ, чем стараться подогнать ее неверные результаты под реальные рынки.

Напомню об одном из возможных подходов к такой модификации.

1.            Собираем статистику — набор исторических пар {d(Fut),d(ImpVol)};

Где d(Fut) – дневное приращение БА

d(ImpVol) – приращение волатильности опционов на центральном страйке за тот же день.

Строим диаграмму приращений, получится что-то вроде того, что на рисунке 1

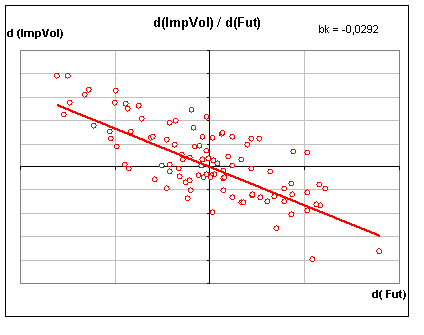
Рис.1

Простой взгляд на картинку подводит к мысли о том, что волатильность можно представить линейной функцией цены базового актива. Исходя из этого, положим σ(F)=a+bF, где F – стоимость БА; a,b – некоторые константы, которые подбираются для конкретного рынка.

2.            Идем к уравнению в частных производных, которое решали БШ.  

В соответствии с предположением заменяем  σ2  на (a+bF)2 .

3.            Решаем полученное уравнение и получаем новые соотношения для справедливой цены опциона.

4.            Пробуем с их помощью описать реальные рынки. Подбираем параметр a (он определяет высоту центральной точки), затем параметры bp,bc по отдельности для ветвей Call, Put (они определяют кривизну ветвей). Получится так, как на рис.2

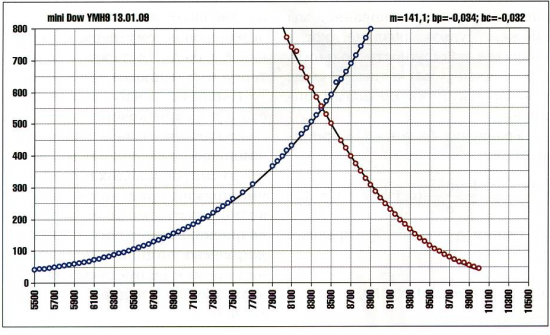
Рис.2 

Все. Никакая кривая IV не понадобилась. Если полученная точность не устраивает, выберите другую зависимость σ(F), или σ(F,t). Или, если полагаете, что коэффициент наклона b не константа, а случайная величина, рассмотрите стохастическое уравнение. Это все вполне решаемые задачи. Во всяком случае, вопрос о том, как правильно посчитать дельту, отпадет сам собой.

PS.  Я не привожу здесь свои формулы. При их выводе в качестве меры активности БА использовалась не волатильность, а подвижность. Они хоть и связаны друг с другом взаимно-однозначным соответствием, но нелинейным, поэтому получить из одной формулы другую просто так не получится, а решать все заново не хочется.