О «теореме Ферма» теории вероятностей или о нормальности «бытия» (много буков)

Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

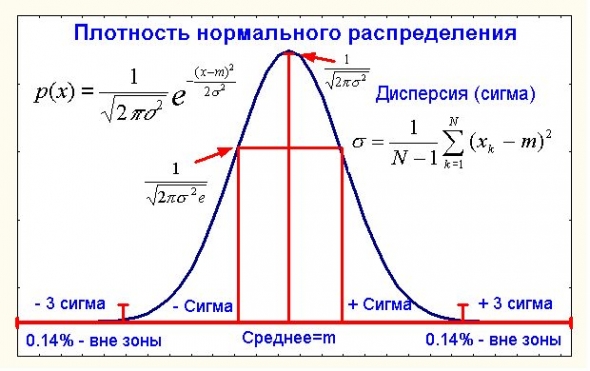
А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x _i, а D – сумма дисперсий тех же величин. Так как дисперсии конечны и не нулевые, то существуют две положительных константы C₁<C₂ такие, что для любого i дисперсия х_i лежит в интервале [C₁;C₂], а для D имеет место неравенство C₁N≤D≤C₂N.

А вот последнее неравенство, из-за которого и появилось в названии теоремы прилагательное «центральная», приводит нас к достаточно интересной задаче, будоражащей умы специалистов в теорвере.

 В 20 веке со времен появления цепей Маркова человечество озаботилось аналогичной задачей   приближения и для случая зависимых случайных величин. Было придумано несколько видов зависимостей, для которых ЦПТ тоже верна. Например, она верна для известной модели Бокса-Дженкинса в наиболее интересных с точки зрения практики случаев. Но для всех таких случаев для дисперсии Х выполняется упомянутое выше неравенство C₁N≤D≤C₂N, правда, с менее четко определяемыми константами C₁ и C₂.

Это, с одной стороны. С другой, для случаев, когда D=CN^k, где k не равно единице, есть куча теорем, когда распределение X близко к совсем другому распределению, а не нормальному. И даже доказывается, что если «близкое» распределение вообще существует, то нормальным оно не будет.  А вот для «центральной» области, т. е. D=CN есть только примеры, когда никакого близкого распределения не существует (или по научному нет сходимости), а все доказанные случаи сходимости только о сходимости к нормальному распределению.

И возникает естественный вопрос о верности гипотезы:

Если распределение Х сходится с ростом N к некоторому распределению и C₁N≤D≤C₂N, то это распределение нормально.

Увы, ее никто не доказал и не опроверг. И целью этой заметки не является обсуждение путей ее решения.

А цель другая: обратить внимание на условие и C₁N≤D≤C₂N. Что такое дисперсия X в общем случаев? Это сумма дисперсий слагаемых плюс сумма попарных ковариаций слагаемых. Понятно, что первая величина в силу конечности  и ненулевости дисперсий принадлежит «центральной» области. А что со второй? Так как дисперсии конечны, то существует положительная константа С такая, что дисперсия любого слагаемого меньше   С. Давайте разделим эту сумму на С и разобьем на три слагаемых: с отрицательными ковариациями, с положительными и с нулевыми. Ну последние нас не интересуют. А что можно сказать про две других? А то, что первая по модулю меньше модуля суммы всех отрицательных попарных корреляций слагаемых, а вторая просто  меньше  суммы всех попарных положительных корреляций.

И что же тогда представляет из себя случай выхода дисперсии за центральную область, т. е. D=CN^k, где k не равно единице? А очень просто:

Если k<1, то среди слагаемых подавляющее большинство  отрицательно коррелированы  между собой и наоборот, если k>1, то  среди слагаемых подавляющее большинство  положительно коррелированы  между собой. Но мы помним, что у независимых случайных величин корреляция нулевая, а значит в обоих случаях  k не равного единице, подавляющее большинство слагаемых зависимо между собой.

И какое это имеет отношение к рынку и ценам? А очень простое. Пусть х_i – это приращение одного тика цены. Если это ликвидный инструмент, то сколько может быть тик внутри дня? Ну 5, максимум 10 шагов цены. Значит его дисперсия точно конечна.

А что такое X? Тоже просто – это приращение цены за N тиков. И когда при больших N Х точно может быть только не нормальным? Если среди тиков подавляющее большинство  положительно (отрицательно) коррелированы  между собой, т. е. зависимы. А что означает зависимость тиков в разные порой далекие моменты времени? А то, что по крайней мере один из  участников тика замыслил это действие во взаимосвязи с большинством других тиков и также  действует один из участников большинства других тиков, т. е. существует достаточно «денежная» группа участников, которые не борятся между собой за «кусок пирога», а «дуют в одну дуду».  

Ну допустим, что N – это тики с открытия торгов до закрытия и рассмотрим уже  Х по дням. И что же тогда, вероятней всего, означает гипотеза о ненормальности Х для почти всех дней. А то, что из-зо дня в день рынком, например, SPY  «кукловодит» какая-то группа очень денежных лиц, хотя и в разные дни это могут быть и разные группы, сменяющие друг друга.

Вы верите, что на SPY такое возможно? Лично я не верю. Но вера – это уже недоказуемо.

А как же тяжелые «хвосты» в выборочном(!)  распределении X по тем же дням, спросит «продвинутый» читатель? А вот это очень просто. Разве N  в разные дни одинаково? А значит никто и не гарантирует стационарности дисперсии нормального закона. Это как минимум. А ведь есть еще и среднее, равное сумме средних тиков. А оно то уж точно разное в спокойные дни и в такие, как 3 марта 2014 или 9 апреля 2018, хотя бы потому что совершенно разные люди в такие дни приходят к одним действиям независимо друг от друга, но под влиянием одиночной внешней новости, т. е. их средние начинают иметь один знак, хотя и корреляции  по прежнему нулевые (методы то разные).

Ну то в америке нормальность, а у нас то точно «кукловодство» — есть такое мнение. А вот и нет. Если «померяться хвостами», то получится, что «наши хвосты» в ликвидных инструментах только пропорционально крупнее, а по виду точь-в-точь как и в штатах. А это значит либо и там и там «кукловодят», либо ни там, ни там. Ну и вопрос выбора между «и-и» и «ни-ни» опять же вопрос веры. Это любой третий вариант – нонсенс и уже ненормальность не в вероятностном смысле.

Как то так не слишком строго и почти без формул «доказывается» то, что приращения цен на больших таймфремах  нестационарно нормальны. А на малых вообще то ограничены. И потому никаких подобий между разными таймфреймами нет и быть не может.  А что это означает? А то, что с «одним аршином» к пятиминуткам  и дневкам подходить надо с очень большой осторожностью  и с недоверием относиться к тем, кто формулирует это в качестве аксиомы.

PS. Дополню тем, что написал в комментарии:  важный гносеологический вывод: если мы строим методы торговли по прошлым дневкам или даже часовикам (если в часах много тиков), то «копать глубже» функций второй степени нелинейности от приращений цен или приращений логарифмов цен (цены в тексте легко меняются на логарифмы цен без потери сути) бессмысленно.