Гипотезы о рыночном базисе

Дисклэймер: далее идет скучный лонгрид.

В 2004-2008 годах мы искали естественное для рынка разложение. Был перебран широкий арсенал от SVD и SSA до спектральных методов типа Фурье-Хаар-вейвлет. Мой кусочек работы был связан с Фурье, Уолшем и вейвлетами. В качестве оценки естественности мы исходили из наивного допущения: что лучше работает, то и естественнее. Лучше — значит обладает лучшими прогнозными свойствами. Т.е., по-простому, какой из базисов позволяет подальше заглянуть (по-честному) в будущее, тот и лучший, стало быть, самый естественный.

Плюс к этому наивному представлению были еще и такие: естественный базис должен не сильно противоречить условиям конечности, нестационарности и т.п. Как это всё проверять? Не очень понятно, но было очевидно, что это необходимо, а также то, что развитая математика не любит нестационарности, конечности, сингулярности и всякое такое прочее.

На 90% рыночным материалом для исследований были данные основных валютных пар (FOREX).

Прежде чем перейти к картинкам, обозначу итоги. Что получилось? Углубиться в проблему, т.е. понять собственное непонимание. Что не получилось? Обрести грааль в виде машинки по печатанию денег. Если оценить без крайностей, то, кажется, что нащупать более предпочтительный базис скорее удалось, чем не удалось. Предпочтительность по косвенным тестам, не по торговому профиту.

Теперь подробнее. Чтобы это было понятно и мне самому, лонгрид будет в стиле комикса. Речь пойдет о демонстрациях преимущества базиса в функциях Уолша над гармониками. Преимущества обнаружены эмпирическим путем исходя из основных методов научного поиска: пальцем в небо и методом тыка. Приводимые примеры не могут претендовать на полноту всех возможных случаев. Однако, случаев преимущества Фурье над Уолшем замечено не было (аналитические преимущества не в счет).

Поскольку с тем, что такое синусоиды, знаком каждый школьник СССР или РФ, а с разложением в ряд Фурье каждый выпускник технвуза и классического университета, про синусоиды напоминать не буду, а про Уолша и Хаара вот такую памятку приведу (ну и про базис тут заодно самые общие формулки):



























Ругательное слово секвента это из секвентного анализа ( Хармут Х. Теория секвентного анализа: основы и применения, М., Мир, 1980), где функции Уолша и Хаара рассматриваются с единых позиций. Там есть очень интересные вещи типа диадной корреляции. Парадокс в том, что для финансов при помощи секвентного анализа у меня не получилось (пока) извлечь профит, но немного набравшись в этих функциях опыта, мы их применили в криптографии, расшифровав один шифр, взламывая файл с данными. Такая вот забава.

Визуально фильтрация может выглядеть так:














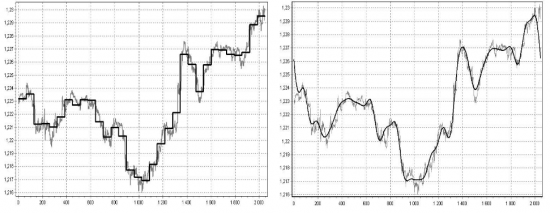
Это если примерно одинаковую часть наиболее значимых компонент (по амплитуде) в спектрах взять. Если взять несколько первых компонент, то фильтрация может выглядеть следующим образом:






















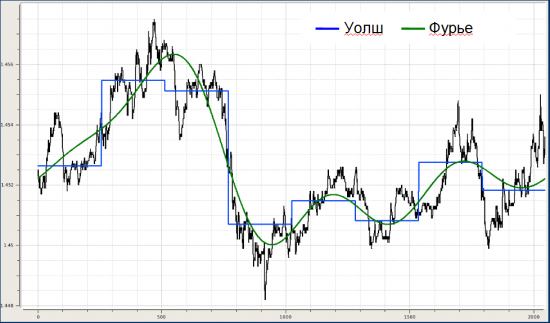
По форме распределние амплитуд Уолш-спектра такое вполне себе нормальное:






















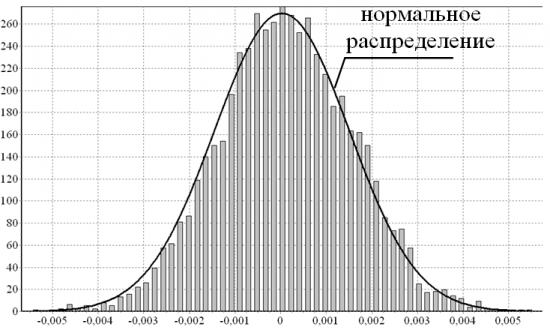
Далее делалась попытка динамического моделирования, чтобы понять, как оно всё адресовано в будущее, если вообще адресовано. Для этого строился динамический след. Берем кусок, делаем два разложения (Уолш и Фурье), запоминаем конец (несколько последних точек), сдвигаем окно разложения на один отсчет, снова фиксируем конец и т.д. Получается картинка такого вида (на примере нулевой+первой функций):






















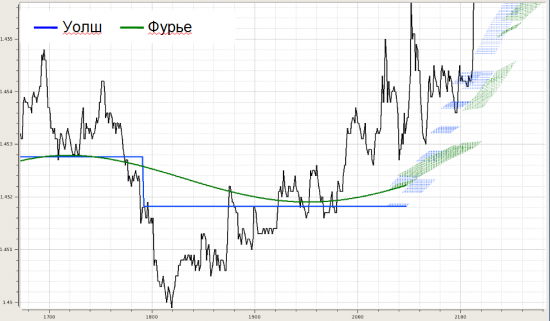
Далее несколько картинок, показывающих, как это может выглядеть для разного кол-ва выбранных функций в фильтрации.
















































































































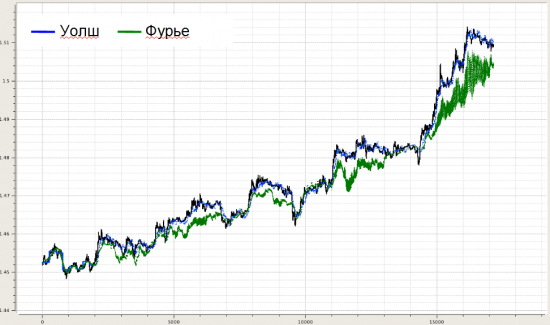
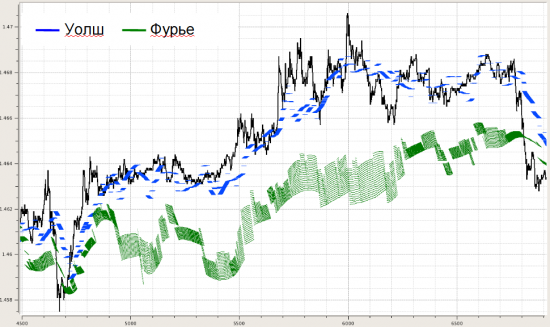
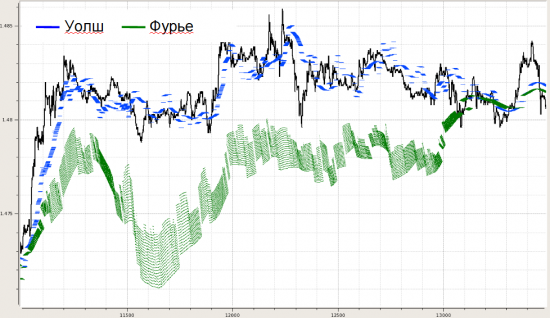
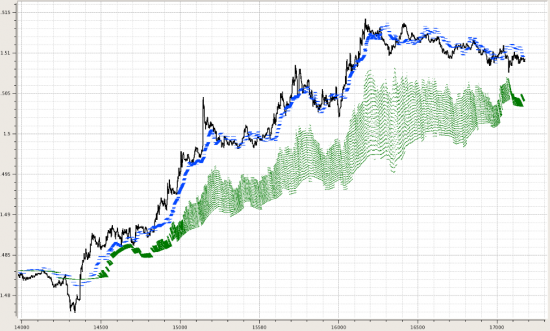
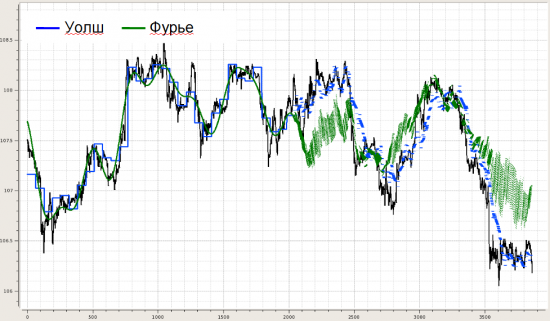
Ну и в плане метрик этого видимого различия строились распределения невязок по концам между реальной котировкой на каждом отсчете и фильтрацией по Уолш- и Фурье-модели:













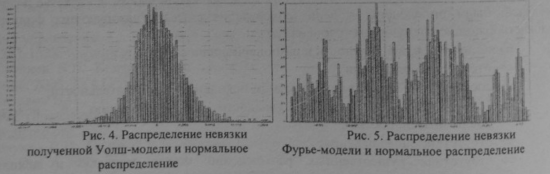
Для Уолша в каждом случае получалось куполообразное распределение с дисперсией, меньшей, чем для дисперсии аналогичной невязки по Фурье.