Quadrat Economy Danilins QED
лишь автоматический перевод русского текста
Обсуждать и даже читать данную статью
руско-говорящим не нужно
и возможно прочитают англо-говорящие
Однако посетители темы могут отметиться на странице статьи
Квадрат Экономии Данилиных QED
kenokeno.ucoz.ru/publ/qed/1-1-0-27
чтобы попасть на карту мира к 30 тысячам посетителей
На странице якобы продаётся книжка сувенир для распечатки
но покупать ничего не нужно хотя я себе распечатал и подарил всем своим
Русская версия на данном сайте
Квадрат Экономии Данилиных QED
smart-lab.ru/blog/458835.php
и данную тему все могут прочитать
Quadrat Economy Danilins QED
Errors should be cheap and cheap
Quadrat Economy Danilins QED was created
at same time personifying asset
and passive because there is no need
to participate in large sums in possible losses.
Applying Quadrat Economy Danilins QED occurs
waiting for a win without major losses and in end
it turns out to wait for events with a coefficient of 100.
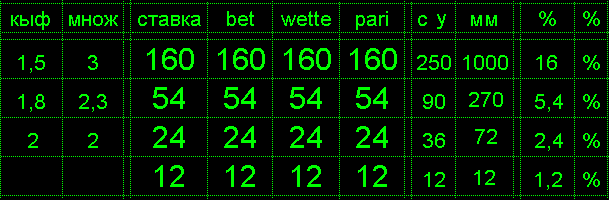
Quadrat Economy Danilins QED filled rates
observing rules of rates saves costs in dozens of times.
Quadrat Economy Danilins QED excluding excitement
personifies a multi-threaded multi-threaded catching up.
Quadrat Economy Danilins
option accelerating where for each
development is higher probability of winning
rates develop horizontally with equal rates
and vertically raising rates to a higher level
and again move to horizontal bets with win
at any point absorbs in column all losses below.
Quadrat Economy Danilins with constant probabilities to guess
with constant bid multipliers when you win after losing
lead to an increase in winnings
Quadrat Economy Danilins with variable probabilities to guess
with variable bid multipliers when you win after losing
lead to a decrease in winnings
despite the theory of a single bet at 1 time
2 bets are possible in 1 time, provided that the win
and losing the bet leads to the next bet in the lower horizontal
strategy of dogon is used and coefficient is catching up.
Play amount of losses possible for several wins
and going into a plus is better not to win back former losses.
In general, mathematical financial management:
lowering of coefficient and increase in probability of winning
and raising rates by a factor dependent on coefficient.
For coefficient K, multiplier of rate M=1+(1/(К-1)).
For coefficient K = 3, multiplier of rate M=1+(1/(3-1))=1,5.
For a probability of about 1/3, limit of mismatch in a row
is equal to D = 12 and at an initial rate of 1% on 12th move
rate should be «1% multiplied by M = 1.5 to power of 12»
and resulting rate should be 130% of balance.
multiplier of increase of next bet depends on coefficient.
from probability depends on number of bets before losing balance.
Mathematical laws are valid in all lotteries and
It is important to know a dozen limits of mismatch in a row by heart.
Multiplication of constant probabilities C+р^N=1 gives formula
N = LOG(1-C)/LOG(1-p)
C is probability of winning guaranteed
p is probability of winning an event.
For example, problem: number of mismatches in a row
with a probability of 99% for probability of 48.65%
N = LOG(1-0,99)/LOG(1-0,4865) = 7
and therefore probability of about 50%
easy to guess 7 times in a row
Simplified it is possible to calculate by formula N = 7+(5*(1/x-2))
for example, x = 0.1 N = 47 is normal and x=0.78 N=4 is normal.
Same formulas are valid for probabilities above 50%.
Geometric progressions containing in condition or in solution
meaning «to what extent it is necessary to erect» is solved through logarithm.
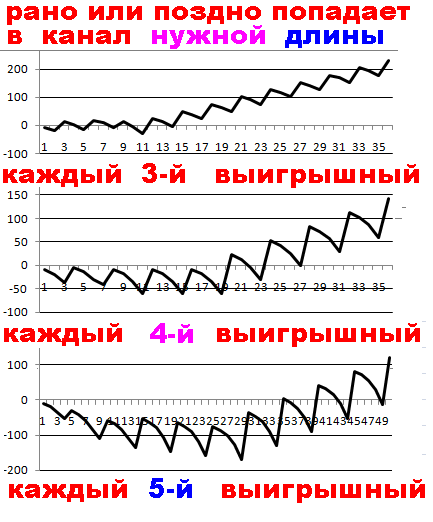
Using discrepancy limit in a row in tables
there is a wave or a guessing period of 2 types:
1st type: wave or period — like probability itself
through number of runs and there where probability of 1/3
there is a wave or guessing period in 3 draws;
2nd type: wave or period — as limit of inconsistencies in a row
and where probability of 1/3 there is a wave or guessing period
in 12 runs and maybe several bets on signal.
There are emulators showing how dynamically developing
Quadrat Economy Danilins QED and subject to zeroing
bet values and when you stop when you reach winnings
Quadratic Economy of Daniline QED shows winning
even when applying same data
To study every third of roulette.
schedule of rates using Quadratic Economy Danilins
looks like a fractal consisting of waves of constituents
a large wave and same graph is obtained
when using mathematically grounded game systems.
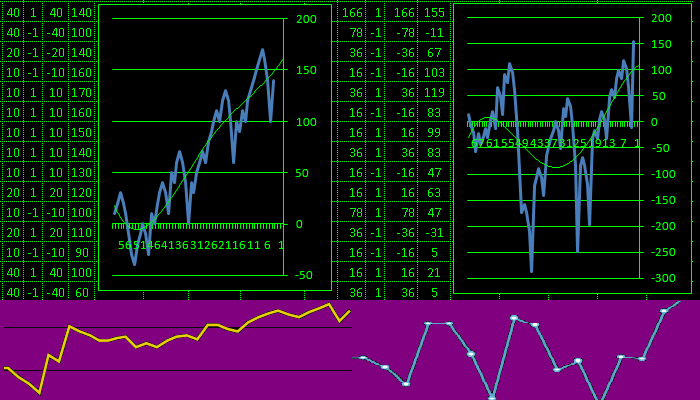
in my themes develops QEDbasic
and brainstorming seeks to recognize spires
and while adding counters of luck and failure
and calculate division of mismatches in a row
QEDbasic recognizes a spire less than previous one
updated QEDbasic constructing Quadrat Economy Danilins
creating textual reports and possibly adding everything
inside of one of reports, QED animation is right I hope
feature: is probability and multiplier
and then there are options for entering a multiplier or plus / minus 10%
number is read from array and the
from 1 to desired number and for other options it is possible to change
source data with offset or re-create an array of numbers
we see characteristic types of graphs with angles and more important than waves
on graphs array under test is on probabilities 1: 2 3 4 1.5 1.33
and how we see problem in temporary inability of QED emulator
Recognize spires leading to zeroing of QED only at maximum
But on air a person can reset Quadrat Economy Danilins
in my themes develops QEDbasic
and brainstorming seeks to recognize spires
and while adding counters of luck and failure
and calculate division of mismatches in a row
QEDbasic recognizes a spire less than previous one
updated QEDbasic exploring spires
It was easier to implement division of 100 copies
and in each segment to look at 6 situations from them 4 promising
and in principle according to schemes around letters in picture is clear
small segments were worse and some spires and all spires
dragged down schedule for any numbers
further I investigate on different probabilities
and learn how to apply division of mismatches in a row
but so far perspective has turned out to be spire132:
balance: lowest / highest / average
as a reduction in balance of seeing a local spire
zeroing only vertical of QED
at spire132: small-many-medium
shows prospects of research
in this case, number 2 for 18/37 numbers
1. array of numbers prepared
2. array of numbers inverted
3. and 4. random numbers arrays
and then I investigate on other probabilities
but each option calls a tree of options
spire132 suggests: start and watch maximum and
spire was almost literally: half between
beginning and maximum then zero column QED
signifier won spire and put a little more on
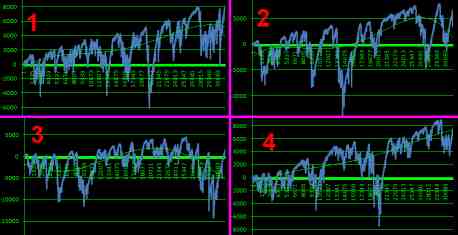
confirmation of my theory
when there is a favorite odd more often
because there is no share of even draws
especially using Quadrat Economy Danilins
Quadrat Economy Danilins contains
points of loss X and points of winning X^2-X
from which it is possible in future
to calculate coefficient return and
investment returns for each
variant of QED depending on side of QED
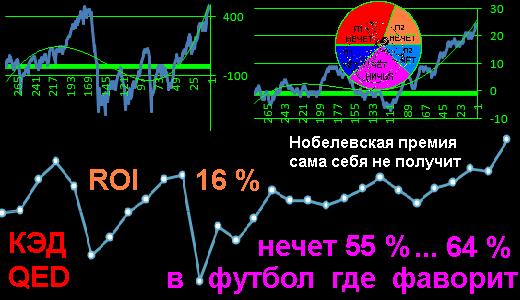
Nobel Prize will not receive itself
















30-тысячным посетителем
моего сайта: живая карта
www.revolvermaps.com/livestats/locations/3nhyjy290s4/
где есть даже Кремниевая долина почти 1000 посещений
и на всех сайтах рекомендую живые карты
and an hour later someone bought a book on my site
graphical representation of benefits of QED:
all possible 64 options 6 cases guessed / unsolved
dogon: maximum: 6 & minimum: -63
Quadrat Economy Danilins: maximum: 6 & minimum: -9
for bets with any factor
wins back all previous losses
vertically with a given win
and it is possible to enter required profit
When winning vertical is reset
and all columns to right are shifted to left
Perhaps apply your rules
for example fill horizontal first
or when winning by removing wager back
Formulas used:
=IF(C3=0;0;(10+SUMM(D4:D$7))/(C3-1))
=IF(C3=0;0;C3*D3-SUMM(D3:D$7))
http://kenokeno.ucoz.ru/gif/qednov18.gif
формула включающая логарифм вытекает из расчёта
вероятности угадать подряд события равновероятные
Например простейшее: 0,7*0,7*0,7 = 0,7^3 = 0,343
в какую степень надо возвести 0,7 чтобы получить 0,343
и в 20-м веке формулу восстановил Андрей Данилин
N = LOG(0,343)/LOG(0,7) = 3
и соответствующая формула для неугадывания
Умножение постоянных вероятностей C+р^N=1
и в 20-м веке формулу восстановил Андрей Данилин
N = LOG(1-C)/LOG(1-p)
С — вероятность выигрыша гарантированного
р — вероятность выигрыша события.
Например задача: число несовпадений подряд
с вероятностью 99% для вероятности 48,65%
и в 20-м веке формулу восстановил Андрей Данилин
N = LOG(1-0,99)/LOG(1-0,4865) = 7
и значит на вероятности около 50%
легко неугадать 7 раз подряд
Упрощённо можно рассчитывать:
формулу открыл Андрей Данилин
N = 7+(5*(1/x-2))
например х=0,1 N=47 нормально и х=0,78 N=4 нормально.
Те же формулы справедливы и для вероятностей выше 50%.
Investigating logarithm is obtained:
formula including logarithms follows from calculation
probabilities of guessing consecutive events
For example, simplest: 0.7*0.7*0.7 = 0.7^3 = 0.343
in what degree it is necessary to build 0.7 to get 0.343
formula restored Andrey Danilin from Russia
N = LOG(0.343)/LOG(0.7) = 3
and corresponding formula for non-guessing
Multiplication of constant probabilities C+p^N=1
gives formula restored Andrey Danilin from Russia
N = LOG(1-C)/LOG(1-p)
C is probability of winning guaranteed
P is probability of winning an event.
For example, task: number of mismatches in a row
with a probability of 99% for probability of 48.65%
formula discovered Andrey Danilin from Russia
N = LOG(1-0,99)/LOG(1-0,4865) = 7
and therefore probability of about 50%
easy to guess 7 times in a row
Simplified can be calculated by
formula discovered Andrey Danilin from Russia
N = 7+(5*(1/x-2))
For example, x=0.1 N=47 is normal & x=0.78 N=4 is normal.
Same formulas are valid for probabilities above 50%.