25 февраля 2018, 15:21
Функция нормального распределения в формулах стоимости опционов
Попробую доступно показать, откуда берется в формулах стоимости опционов функция распределения Гаусса.
Итак исходное уравнение Блэка-Шоулза:
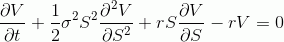
где V — цена опциона, S — цена спота, r — ставка, ну и сигма в представлении не нуждается.
Это параболическое дифференциальное уравнение в частных производных. Решать можно несколькими способами, но я не буду этого делать, а сразу запишу решение, т.к. его вывод не имеет значения для цели этого топика.
Чтобы слегка упростить запись, введу переменную времени, оставшегося до экспирации:
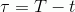
Решение уравнения БШ тогда можно записать в следующем виде:
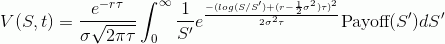
где Payoff(S) — это функция выплат опциона. Для опциона кол:
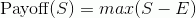
Соответственно цена кола:

поменяем переменную интегрирования на
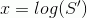
тогда
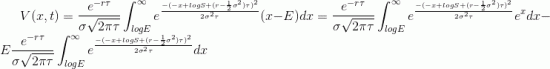
Считать стоимость опциона по этой формуле не очень просто, но рассмотрим сначала второе слагаемое:
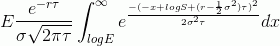
Сложно не заметить сходство с функцией нормального распределения:
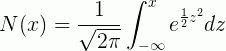
В силу популярности нормального распределения для этой функции существует немало аппроксимаций и способов вычислить ее численно. Та или иная реализация имеется, без преувеличения, в любом статистическом пакете.
Если нам удастся выразить второе слагаемое через эту функцию, то считать стоимость опционов будет намного легче. Так что овчинка стоит выделки!
Заменим переменную интегрирования во втором слагаемом выше на
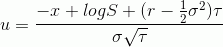
и получим
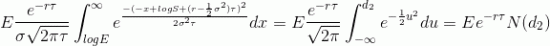
где

С первым слагаемым не так очевидно, но все же не очень сложно. Сначала надо подвести дополнительное слагаемое в экспоненте под квадрат, а далее действуем аналогично второму слагаемому. Поэтому здесь я сразу запишу результат:
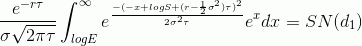
где
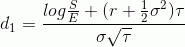
В итоге получаем, что хотели:

Ну теперь уж должно быть очевидно, что функция распределения Гаусса в формулах стоимости опционов БШ не более чем очень удачный способ упростить вычисление интегралов в исходном решении уравнения БШ.
Это очень элегантная техническая деталь но тот факт, что дельта опциона выражается через N(x) — всего лишь следствие записи производной от V(S,t) по S с использованием преобразований, аналогичным использованным выше, и никакого отношения к вероятности выхода опциона в деньги он не имеет.
Итак исходное уравнение Блэка-Шоулза:
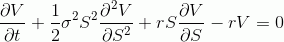
где V — цена опциона, S — цена спота, r — ставка, ну и сигма в представлении не нуждается.
Это параболическое дифференциальное уравнение в частных производных. Решать можно несколькими способами, но я не буду этого делать, а сразу запишу решение, т.к. его вывод не имеет значения для цели этого топика.
Чтобы слегка упростить запись, введу переменную времени, оставшегося до экспирации:
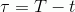
Решение уравнения БШ тогда можно записать в следующем виде:
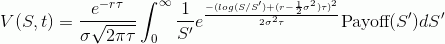
где Payoff(S) — это функция выплат опциона. Для опциона кол:
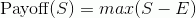
Соответственно цена кола:

поменяем переменную интегрирования на
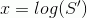
тогда
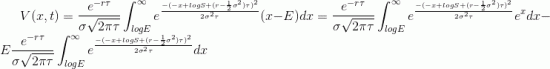
Считать стоимость опциона по этой формуле не очень просто, но рассмотрим сначала второе слагаемое:
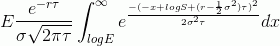
Сложно не заметить сходство с функцией нормального распределения:
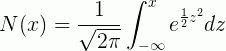
В силу популярности нормального распределения для этой функции существует немало аппроксимаций и способов вычислить ее численно. Та или иная реализация имеется, без преувеличения, в любом статистическом пакете.
Если нам удастся выразить второе слагаемое через эту функцию, то считать стоимость опционов будет намного легче. Так что овчинка стоит выделки!
Заменим переменную интегрирования во втором слагаемом выше на
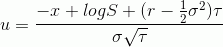
и получим
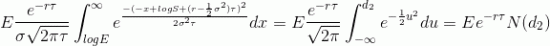
где

С первым слагаемым не так очевидно, но все же не очень сложно. Сначала надо подвести дополнительное слагаемое в экспоненте под квадрат, а далее действуем аналогично второму слагаемому. Поэтому здесь я сразу запишу результат:
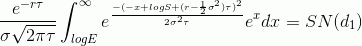
где
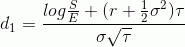
В итоге получаем, что хотели:

Ну теперь уж должно быть очевидно, что функция распределения Гаусса в формулах стоимости опционов БШ не более чем очень удачный способ упростить вычисление интегралов в исходном решении уравнения БШ.
Это очень элегантная техническая деталь но тот факт, что дельта опциона выражается через N(x) — всего лишь следствие записи производной от V(S,t) по S с использованием преобразований, аналогичным использованным выше, и никакого отношения к вероятности выхода опциона в деньги он не имеет.
Читайте на SMART-LAB:

Какие инвестидеи открывает война в Иране: видеообзор аналитика Т-Инвестиций
Какие инвестидеи открывает война в Иране: видеообзор аналитика Т-Инвестиций
Новая война на Ближнем Востоке может пойти по разным сценариям — от этого зависит, какие активы и как будут...
13:17
🛒 Фикс Прайс остался без "органики"
Ретейлер представил отчет по МСФО за 4 квартал и весь прошлый год Фикс Прайс (FIXR) ➡️ Инфо и показатели Результаты за 4 квартал — выручка: ₽85,5 млрд (+2,6%) — скорр....
13:00












я мехматов не кончал, хотя и прослушал два курса по высшей математике, слишком давно было, ничего уже не помню.
Дельта может и не равна вероятности выхода опциона в деньги. Но очень сильно с ней коррелирует, так?
И вообще, если вокруг опционов построена такая обширная математическая модель, неужели нет ни одного грека, который бы показывал вероятность выхода опциона в деньги? Не дельта ли ближе всего к этой вероятности?