Статистические модели трендов. Смещение среднего. (Дополненное)

Попросили объяснить что такое персистентность без специальных терминов и как она связана с трендовостью рынка. Совсем, без терминов вряд ли получится, но если их минимизировать, достаточно понятия — плотности вероятности. 

Что такое плотность вероятности? Это функция интеграл интервала которой, дает нам вероятность попадания в этот интервал. Или в простейшем случаи, если мы рассматриваем ее эмпирическую оценку в виде гистограммы распределения это будет просто частота попадания в набор фиксированных интервалов. 
Для примера рассмотрим гистограмму нормального распределения.

 

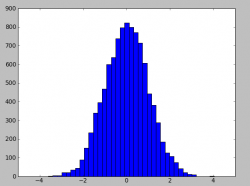
Собственно что мы видим — разбиение на набор фиксированных интервалов, затем подсчет попадания каждого значения в тот или иной интервал, который дает частоту. Если мы хотим посчитать частоту попадания в бОльший интервал например от 0 до 2, то нам необходимо сложить(проинтегрировать) частоту попадания во все маленькие интервалы внутри этого отрезка [0, 2]. Таким образом плотность вероятности дает возможность, зная интервал, получить вероятность попадания в него. Или если рассматривать на более «интуитивном» уровне — показывает какие значения выпадают более часто, а какие менее. В приведенном примере, наиболее часто выпадают значения вокруг нуля распределения и затем оно постепенно спадает. 

Если мы рассмотрим, распределение как набор значений расположенных во времени (привычные для трейдинга представления в виде графиков числовых рядов). То получим для все того же нормального(гауссового) распределения следующую картинку:


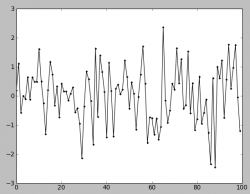
Как и ожидалось из гистограммы распределения, 95% значений находятся внутри интервала от -2 до +2, с центром в нуле. 

Каждый наверняка видел график случайного блуждания и этот на него мало похож. Разница в том, что для того чтобы получить случайное блуждание необходимо последовательно сложить эти значения. Или наоборот чтобы получить из случайного блуждания — распределение приращений, необходимо взять разность соседних значений. 

Таким образом мы подходим к первой простейшей модели тренда. Рассмотрим распределение приращений: 


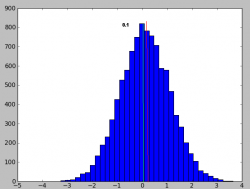
которое практически на глаз не отличается от предыдущего, но среднее (центр) сдвинуто на +0.1. Теперь просуммируем значения распределений для первого случая с нулевым и положительным (+0.1) смещением среднего, таким образом получим два графика случайных блужданий. 

Первый, без смещения в мат ожидании приращений:


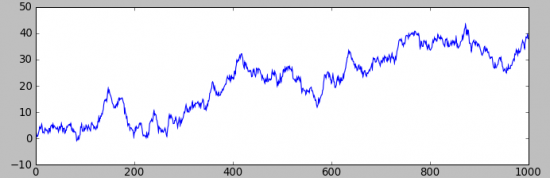
А второй, с «ничтожным» (ели разлечимым на графике распределения приращений) смещением(+0.1):


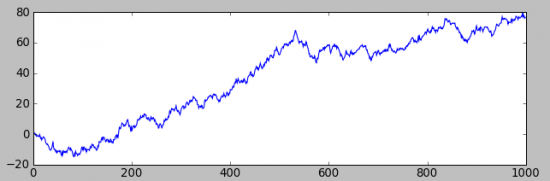
Разница, разительная, но на первом графике — заработать не возможно, а на втором вполне. 

В данном случае мы рассматриваем, зависимость(смещение в мат. ожидании), которая не изменяется во времени, то есть стационарна, 0 для всего графика, или +0.1 другого. Теперь представим что эти значения сами изменяются во времени, и представляют к примеру кусочно-постоянную функцию. То есть набор констант, из которого мы выбираем значение, действующее на каком-то интервале. Соответственно если это значение положительное возникает «растущий кусок тренда», если отрицательное — «падающий». А сам график «сшит» из таких интервалов с  постоянными значениями. Таким образом мы получим приближенную к реальности простейшую динамическую модель тренда. У которое стационарное среднее приращений равняется 0, но при этом существуют интервалы на которых оно отклоняется от 0 как в положительную так и отрицательную сторону. При этом в среднем количество таких участков «уравновешивается» и мы получаем среднее всех приращений близким к нулю.

Или если мы будем рассматривать среднее, как функцию времени, то для кусочно-постоянной модели, получим следующую картинку:

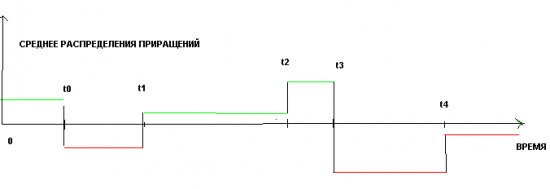
Или ввиде формулы, P_i+1 = P_i + A_k + N(0, 1)  , где A_k это значение среднего на данном временном интервале(t_k, t_k+1), N(0, 1) стандартизированное нормальное распределение, а Pi это получившийся стохастический процесс. 

Для примера рассмотрим реализацию такого стохастического процесса, при t_k = (0, 100, 200, 400, 450, 600, 650) и A_k = (+0.1, -0.1, +0.05, +0.15, -0.2, -0.05), что примерно соответствует представленному выше графику зависимости от времени. 

Первая реализация:


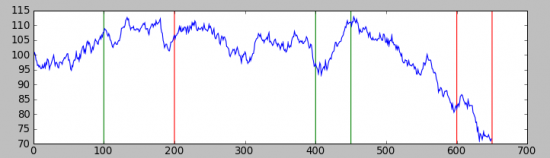
Вторая реализация:


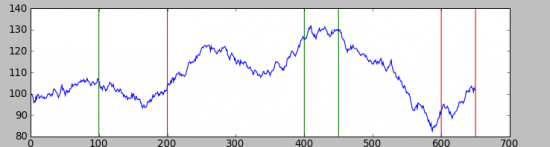
Как видно они мало похожи, и в них гораздо менее очевидно наличие трендов чем в простейшем стационарном случаи, но тем не менее они там присутствуют, а значит на таком процессе возможно заработать.

В следующей серии, мы поговорим о еще одной модели тренда, которая связана с персистентностью, или более конкретно, мы будем понимать под персистентностью — авто-регрессивность числового ряда.