Отдаю грааль в добрые руки

Картинка для затравки, Out of Sample perfomance (то есть результаты получены на выборке на которой не производилось построение модели):


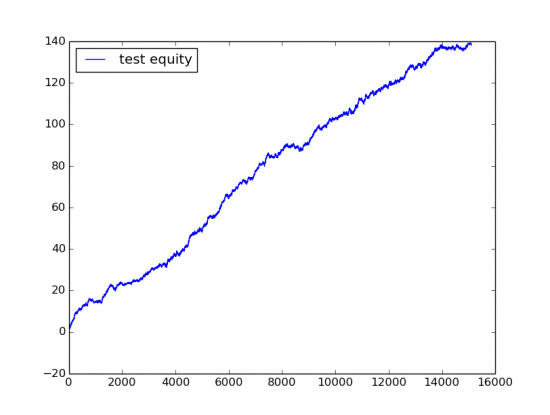
Сбербанк MOEX 15106 трейдов прибыль 140 руб на одну акцию, периодичность трейдов где-то 15 минут, equity где-то за год.
То же самое для Ri, 22237 трейдов прибыль 100000 пунктов на один контракт, или 5 пунктов на трейд, периодичность такая же 15 минут.

Кому не терпится, выложил исходный код с остальными кратинками (каталог ./img) на github.
github.com/xmvlad/stock_trade_datamine

В чем собственно суть подхода. Начну немного из далека, по большому счету, когда вы пишите стратегия в каком ни буть Wealth-Lab или TS-Lab, она по сути состоит из двух частей Факторов (то есть к примеру индикаторов RSI, ADX или еще чего-то более своеобразного) и некоторой Логики которая на основе факторов принимает решения о том какую позицию занимать.

VC-dimensions и проклятие размерности

Основная проблема построения систем в ручную, то что при увиличении факторов написать для них логику принятия решения становится практически нереально. С другой стороны при построении систем часто используют оптимизацию, но как многим хорошо известно при увиличении количества параметров оптимизации In-Sample и Out-Of-Sample перфоманс системы начинает сильно расходится. Но мало кто понимает что на самом деле проблема не в количестве свободных параметров, а в способе которым они находятся. В статистике есть область, которая изучает способы извлечения зависимостей по данным, это область машинного обучения. Так вот, в ней есть интересные результаты, показывающие почему на самом дели для модели построенной на обучающей выборке(In-sample) ее результаты могут сильно отличаться тестовой(Out-of-sample), при условии что обучаем мы ее некоторой стационарной плотности вероятности. И связано оно со способностью модели разделять точки во входном пространстве параметров, и называется эта метрика VC dimensions(Vapnik–Chervonenkis dimension). В чем ее суть, если мы возьме простейшую линейную модель, например логистическую регрессию, то она будет представлять из себя разделяющую плоскость в N-мерном пространстве входных параметров, для конкретности возьмем что N=10. Что это означает, если в обучающей выборке, меньше 10 точек, то мы всегда можем построить плоскость через эти 10 точек и получить великолепную предсказательную способность на обучающей выборке, которая не будет распросраняться на тестовую. Так же очевидно, что если мы взяли 500 точек, и получили для них хорошую предсказательную способность модели, то есть они все лежат в одной плоскости, то чем больше соотношение количество входных точек к размерности модели, тем больше вероятность, что результат обучающей и тестовой выборки будут сближаться (при условии что мы их считаем на одной и той же плотности). Так вот если для линейной модели, хорошо понятно что при размерности N=10 она задает плоскость в 10-мерном пространстве, и чем ближе к этой плоскости лежат точки тем лучше, то для более сложных моделей этот момент неочевиден, VC-размерность по сути являются расширением понятия «размерности модели» на произвольный случай. Так вот возвращаясь к исходному вопросу, в чем проблема оптимизации алгоритмических стратегий путем перебора параметров, в том что при низком фактическом количестве параметров они имеют очень высокую «размерность модели» (VC-размерность), то есть перебирая некоторые параметры(например индикаторов), мы всегда можем разделить «хорошие» точки от «плохих». Это нас приводит к мысли, что проблема ни в самих свободных параметрах, а в способе построения модели, и хорошо бы найти какой-то «средний» вариант, между простотой линеных статистических моделей и стратегиями имеющими высокую VC-размерность. И такой вариант давно найден и используется в области машинного обучения

Decision trees(Дерева принятия решений)

en.wikipedia.org/wiki/Decision_tree

Не буду расписывать подробно, так как можно прочитать в википедии. Но суть в том, что дерева приняти решения примерно эквивалентны той логики которую можно написать на языке программирования с использованием вложенных if условий использующих различные Факторы. Есть различные способы их построения, но все сводятся примерно к следующему, они пытаются апроксимировать входную плотность вероятности. На основе деревьев принятия решений, строятся некоторые более сложные модели например Random Forest(которые и использовались в данной модели), но суть их остаеться той же. Хотя деревья принятия решений и имеют VC-размерность большую, чем у линейных моделей, которая пропорциональна O(n*d), где — n количестов факторов, d — глубина дерева (для линейных моделей O(n)), но все равно она остается достаточно ограниченной, чтобы при наличии достаточного количества данных модель не переобучалась. В общем, можно применять различные модели, главное сохранять баланс между ее «размерностью», описывающей способностью, и количеством входных данных.

Результат

Собственно, если в двух словах, то как получились картинки из начала поста, по 1 минутным данным строилось большое количество факторов, инидикаторы (RSi, ADX), свечные паттерны, полиномиальная апроксимация скользящим окном. Затем на основе факторов, строилась модель Random Forest с жестко ограниченной VC-размерностью, и регуляризацией. Исходный код доступен по ссылке. Торговать это конечно, из-за профитов съедаемых комиссией нельзя, но возможно кому-то будет интересно как пример работающего low-frequency подхода.