Задача о котировке, которая никогда не вернется

В третьей части цикла статей Виктора Аргонова о теории вероятностей мы наконец переходим непосредственно к фондовому рынку. Парадоксы, которые работают при случайном блуждании пьяного человека и при игре в казино, работают и на биржевом рынке. И зачастую работают неожиданным образом, разоряя незадачливых, а подчас и опытных трейдеров.

Большинство трейдеров знают важное правило биржевой игры: если ты купил акцию, а она подешевела, то не спеши её продавать. Скорее всего, она рано или поздно вернётся на былую позицию, да ещё и пойдёт вверх. Вопрос лишь в том, когда это произойдёт. Очень часто трейдер ждёт месяц, год, десять лет — а цена акции “на место” не возвращается. Вроде бы и фирма не банкрот, и кризисов особых нет — но котировка как когда-то просела, так и “толчётся” недалеко от цены покупки. И скачет по всякому, а возвращаться не хочет. Как будто специально, чтобы тебе “насолить”. Но злого умысла тут нет, а есть очередной парадокс теории игр.

Беспроигрышная игра с нулевой выгодой

Поставим следующую задачу. На бирже есть множество акций с разными ценами. За день цена каждой акции может равновероятно увеличиться или уменьшиться на доллар. Инвестор заходит на биржу раз в день. В первый день он покупает первую попавшуюся акцию в количестве 1000 штук. Затем он ждёт, когда цена акции поднимется на доллар. После этого он продаёт весь пакет акций (получив прибыль $1000) и тут же покупает какую-то новую акцию в том же количестве 1000 штук. Затем он ждёт их подорожания на доллар, тоже продаёт (вновь с прибылью $1000), и так далее.

Предположим, что ни одна фирма разориться не может, даже если цена акций отрицательна. Поэтому игра для инвестора беспроигрышна: при каждой сделке он лишь приобретает выгоду.

Зададим два вопроса.

• Каким будет среднее время ожидания подорожания акции на доллар?
• Каким будет средний доход инвестора?

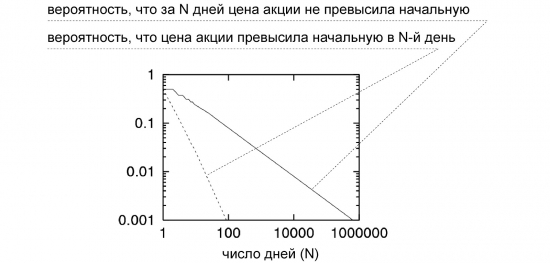
Это новая формулировка всё той же задачи о случайном блуждании точки и времени её возврата к начальному значению (точнее — о пересечении начального значения). И мы знаем, чего здесь следует ожидать. Вновь приведём знакомые графики.

С вероятностью ½ пакет удастся выгодно перепродать уже на следующий день, с вероятностью ⅛ — через три дня, и так далее. Примерно в каждом десятом случае ожидание затянется на 100 дней, в каждом сотом — на 10 тысяч дней, в каждом тысячном — на миллион дней (три тысячи лет). При неограниченном времени игры среднее время ожидания будет стремиться к бесконечности, а средний доход — к нулю.

Хотя эта задача идеализирована, она даже в такой простой формулировке объясняет, почему описанная тактика биржевой игры — не панацея для неограниченного обогащения. Трейдеры знают, что описанная ситуация — это игра на заявке типа Take Profit: продать акцию, как только её цена на указанную величину превысит цену покупки. Эта тактика, действительно, почти беспроигрышна (если не учитывать комиссий), но в чистом виде толку от неё немного. Поэтому попробуем усложнить задачу. Быть может, некоторые новые условия позволят сделать игру выгодной?

Бесконечность можно убрать, а ноль и ныне там

Оставим условия задачи теми же, но введём одно дополнительное ограничение: если акции не подорожали на доллар за X дней, инвестор всё равно продаёт их, пусть и с убытком.

• Каким будет средний доход инвестора?
• При каком X игра наиболее выгодна?

Ограничение на время цикла купли-продажи “разрубает гордиев узел” бесконечных решений, но грозит убытком. Чего будет больше — прибылей или убытков?

Предположим, что инвестор решил отсечь лишь самые длинные “полёты”, установив X=100. Если котировка не вернулась к нужному значению за100 дней (3 месяца), то акция продаётся. Как уже известно из задачи о пьяницах, убыток, скорее всего, составит порядка $10000 (котировки будут находиться ниже начального значения на $10, и таких акций — 1000 штук). Вероятность такого события — примерно 1/10. В остальных 9 случаях инвестор получит выгоду по $1000 за сделку. Получается, что прибыли примерно равны убыткам, и игра не стоит свеч. Те же проблемы будут при любых больших X, когда доля слишком длинных полётов (полётов Леви) пропорциональна квадрату X. Но может быть, игра будет выгодной при малом X, когда степенной закон не работает?

Очевидно, что ставить X=1 нельзя, ибо тогда в одной половине случаев акции будут продаваться с выгодой $1000, а в другой половине — с таким же убытком. При X=3 выгодными будут ⅝ от всех сделок, а невыгодными — ⅜. Прибыль во всех выгодных сделках будет равна $1000. Две трети невыгодных сделок дадут убыток $1000, а одна треть — $3000. Средний выигрыш равен $(5*1000-2*1000-1*3000)/8=$0. И то же получается вообще при любом X.

Ограничить не время, а убытки?

Прочитав предыдущий раздел, практикующий трейдер скажет: наверное, неправильно ограничивать время блуждания котировки, когда можно напрямую ограничить убытки. То есть поставить заявку Stop Loss, которая продаёт акции, цена которых спустилась от начального значения на M долларов. Но степенные законы распределений коварны, и таким ограничением в нашей задаче всё равно нельзя добиться выгоды.

 

Если M=-1, то невыгодно будет продаваться каждый второй пакет акций — это нас не устраивает. При M=-2 ситуация сложнее. С вероятностью ½ инвестор получит выгоду $1000 уже в первый день, но с вероятностью ¼ он получит убыток $2000 во второй день. С вероятностью ⅛ он получит $1000 в третий день, но с вероятностью 1/16 получит убыток $2000 в четвёртый день. Сколько бы мы ни продолжали этот ряд, средний опять выигрыш равен 0. И то же будет при других значениях M. Убыток всегда пропорционален M, а вероятность этого убытка — обратно пропорциональна M. В сухом остатке, средний убыток равен средней прибыли.

Вовремя выйти из игры?

Предпримем последнюю попытку найти выгодную тактику в этой странной игре. Можно поверить, что при бесконечной игре средний выигрыш равен нулю. Ещё понятнее, почему невыгодна игра при “обрубании” полётов с явным убытком. Но почему бы не совершить, например, строго ограниченное число сделок за явно достаточный период времени? Например, 10 сделок за 10 лет. Не “обрубать” полёты котировок, а ждать, сколько потребуется.

На первый взгляд, на интервале в 10 лет должны почти гарантированно поместиться все сделки. Но оказывается, что даже при скромной цифре в 10 сделок это не совсем так. Вероятность, что хотя бы одна сделка продлится дольше 10 лет, составляет порядка десяти корней из 1/3650, то есть 0.1676. А это немало. Впрочем, едва ли затянувшаяся сделка будет в этой череде первой. Есть ненулевая (и весьма большая) вероятность, что инвестор всё же успеет совершить несколько сделок. И все они будут с положительной выгодой.

Значит, средний ожидаемый доход всё же положителен? Увы, в наши рассуждения вкралась ошибка. Мы не разобрались, что будет, если одна из позиций всё-таки осталась незакрытой. А это, фактически, означает долг. И если всё аккуратно вычислить, то вероятный размер этого долга составит ровно столько, сколько инвестор успел заработать. Точно как в случае, когда мы “обрубаем” затянувшийся возврат.

Итак, наши попытки найти заведомо выигрышную тактику в данной игре напоминают поиск “вечного двигателя” — попытку обмануть тот простой факт, что скачки котировок полностью случайны и движение вверх и вниз равновероятно. Это типичная игра с нулевой суммой.

Ближе к реальности

Теперь необходимо всерьёз поставить вопрос: какое отношение все эти рассуждения имеют к реальности? Задача о пьяницах была шуточной и содержала грубые упрощения. Задача о казино была уже более серьёзной, так как казино может строго задать даже самые вычурные правила. Но всё-таки она касалась игры. А когда мы рассуждаем о котировках, стоит вопрос о работе реального финансового мира, работе производств, распределении богатств и т. д. И если бы рынок действительно работал как описанный генератор случайных чисел, то играть на колебаниях цен было бы бессмысленно. Успешных профессиональных трейдеров не могло бы существовать. Все трейдеры были бы не более, чем игроками в казино.

Но реальная жизнь — это не идеальная математика и не казино. Вот лишь несколько отличий.

• На реальном рынке не бывает бесконечных денег.
• Реальные фирмы могут разоряться.
• При реальной торговле брокер берёт за сделку комиссию
• Реальные акции могут давать дивиденды.
• Реальная статистика скачков цен не полностью случайна, ибо есть политика и многое другое.
• На реальных котировках бывают не только долларовые скачки, а какие угодно.
• На реальных котировках, помимо случайного движения, существуют циклы.

Некоторые из этих факторов (дивиденды, циклы, зависимость рынка от политики) облегчают жизнь трейдера. Но некоторые (комиссии, разорение фирм) — усложняют.

Главный проблемный факт, который есть не только в идеализированных моделях, но и в реальной торговле — это степенная статистика времён возврата цен на прежние позиции (и полёты Леви). Колебания на реальном рынке не совсем случайны, но если мы многократно отследим времена возврата котировок к начальному положению, мы получим знакомые нам графики, которые выглядят как прямые в дважды логарифмическом масштабе. Действительно, котировки чаще всего возвращаются через короткое время. Но если не возвращаются долго — то на них можно махнуть рукой.

Благодаря быстрым внутридневным циклам в течение дня цена акции может несколько раз вернуться на прежнее место. И этим активно пользуются так называемые скальперы: купил акцию по цене $50, через секунду она стала $49.99, а ещё через секунду — $50.01. Скальпер продал её и получил выгоду. Выгодный скальпинг возможен благодаря неполной случайности колебаний и наличию циклов. Но и здесь необходимо помнить о возможностях больших полётов. Если скальпер утратил внимание, а цена акции случайно просела на целый доллар (в 100 раз сильнее, чем он рассчитывал), то не стоит думать, что она вернётся через 100 секунд. Если тренд будет положителен, она вернётся через 10000 секунд, а если отрицателен — то может просесть на десятилетия и века. А для трейдера, который хочет заработать здесь и сейчас — это не слишком отличается от бесконечного времени возврата.

Не только в идеализированной задаче, но и на реальном рынке цена, далеко отошедшая от начального положения, может колебаться там сколько угодно. Её ничто не “тянет” обратно. Если говорить в математических терминах, в начальной точке нет никакого аттрактора, она ничем не лучше других. Есть вероятность, что котировка будет возвращаться бесконечно долго. И если при идеальном случайном блуждании вероятность этого бесконечно мала, то в реальном мире вероятность невозврата конечна, например, потому что фирма может обанкротиться.