22 декабря 2011, 19:55
Ценная подборка №33. К вопросу об уровнях. Часть вторая
Современная западная экономическая теория и теория финансов, как ее часть, держится на понятии равновесия, которое понимается как точка баланса между интересами различных групп экономических агентов, действующих на рынке. В случае цен на рынке товаров и услуг равновесной оказывается такая цена, при которой уравниваются спрос и предложение и в практической экономике достаточно много разработанных методов определения таких цен на реальных рынках. Казалось бы, финансовые рынки, как частный случай рынков вообще, тоже должен управляться данным механизмом. Однако, две, предъявляемые в теории финансов парадигмы равновесия, оказываются довольно зыбкими.
Первая – это, естественно, т.н. «справедливая цена» акций, вычисляемая из фундаментальных показателей (в первую очередь, потока будущих платежей). Если все вычисляют эту цену одинаково, то она и является равновесием, которое должно устанавливаться на рынке после появления новых фундаментальных данных. На практике же, оказывается, что различия в методах вычисления и конкретных параметрах (например, стоимости денег, или прогнозах потоков платежей) приводят к тому, что оценки, приводимых разными, безусловно, авторитетными аналитиками, могут отличаться в два раза. Впрочем, это было вполне приемлемо с точки зрения соответствия теории наблюдениям, если бы реальная цена большую часть времени проводила бы в коридоре, обозначенном аналитиками и/или колебалась возле консенсуса. В реальности мы видим совсем иное поведение – цена практически всегда находится очень далеко от консенус-прогноза и очень часто даже не попадает в коридор, определяемых фундаментальными оценками. Более того, внимательный анализ показывает, что примерно в половине случаев изменение фундаментальных прогнозов происходит после резких изменений цены (а не наоборот, как должно быть согласно теории).
Вторая парадигма объявляет равновесием текущую цену, ссылаясь на изобретенную еще Доу формулу: «цена учитывает все». При этом фундаментальная информация оказывается далеко не «всем», чем и объясняется сильное отклонение текущей цены от фундаментальной. В текущей цене с точки зрения сторонников этой парадигмы не менее важную роль играют настроения, слухи и ожидания на их основанные, которые и вносят в итоге весомый довесок в положение равновесия. Основная претензия к этой парадигме очевидна: можно ли считать равновесием нечто, что может изменяться столь быстро и столь же непредсказуемо, как цена акций?
Так существует ли равновесие на рынке? Можно ли найти какую-то здравую величину между практически никогда не достижимой фундаментальной ценой и слишком непредсказуемой текущей? Оказывается, можно. Для этого проведем забавный мысленный эксперимент. Представим себе много участников рынка, которым в начале игры раздали деньги и акции (все акции одинаковые). Кому-то только деньги, кому-то только акции, кому-то акции и деньги в разных пропорциях. Далее запустили обычный аукционный процесс торговли, обеспечили поток новостей на рынок и поставили целью участников заработать как можно больше денег к моменту «Х», который, допустим, заранее неизвестен. Когда на этом «рынке» установится нормальный торговый режим, объявим час «Х», после которого торги будут прекращены навсегда Портфель каждого участника будет оценен по последней цене торгов. Тем, кто закончит торги с суммой портфеля больше начальной будет выплачен весь полученный доход за счет тех, чьи портфели будут иметь оценку портфеля ниже начальной (понятно, что в такой замкнутой системе сумма проигрышей и выигрышей окажется одинаковой). Можно ли предсказать на какой цене закроется рынок в час «Х»? Оказывается, можно!
Проделаем несколько странных на первый взгляд процедур. Во-первых отсортируем все сделки, прошедшие на рынке по возрастанию от самой низкой к самой высокой. Во-вторых, просуммируем объемы сделок нарастающим итогом начиная с самой низкой цены. В третьих, просуммируем объемы сделок нарастающим итогом начиная с самой высокой цены. В результате мы получим две кривых. Одна будет увеличиваться при росте цены, вторая, наоборот уменьшаться при росте цены:
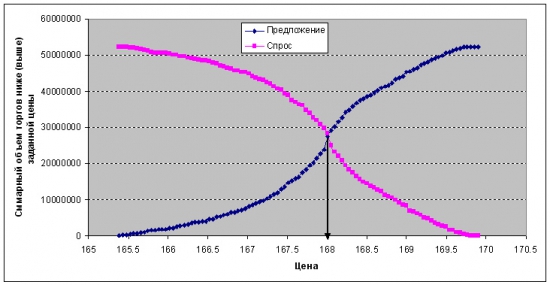
Рисунок получен по тиковым данных торгов акциями ОАО «Газпром» 22.08.11 с 10.30 до 16.00
Что будет происходить на нашем модельном рынке с момента объявления часа «Х»? Все, купившие акции ниже текущей цены будут стараться продать их, чтобы зафиксировать прибыль, а все продавшие акции выше текущей цены будут стараться купить акции, чтобы тоже зафиксировать имеющуюся прибыль. Соответственно две полученных выше кривых можно будет трактовать как кривую предложения акций (суммарный объем акций, купленный ниже текущей цены, будет выставляться на продажу для фиксации прибыли) и кривую спроса на акции (суммарный объем акций, проданных выше текущей цены, будет выставляться на покупку для фиксации прибыли). В экономике хорошо известна цена, к которой в итоге сойдутся торги – она будет определяться точкой пересечения кривых спроса и предложения. В приведенном на рисунке примере это будет цена около 168 рублей.
Итак, на модельном рынке, где известна дата окончания торгов можно определить цену к которой в итоге сойдется торги и в этом смысле такую цену можно считать равновесной (т.е. ценой к которой будет стремиться рынок в отсутствие новостей). Любопытно, что эта цена будет зависеть от траектории торгов и распределения объемов.
Имеет ли отношение рассчитанная таким образом равновесная цена к поведению реального рынка? Отдельные, рассчитанные описанным выше образом, цены на разных горизонтах я называю «локально равновесными» или просто «равновесными», а их набор «модернизированной планитерией» и занимаюсь по мере появления времени исследованием свойств этих цен или «уровней». Что понятно на текущий момент. Начнем со свойств одной равновесной цены, рассчитанной по произвольному фиксированному интервалу. На текущий момент понятно, что:
1. Равновесная цена является достаточно медленно изменяющейся функцией по сравнению с текущей ценой.
2. Равновесная цена является областью «отталкивания» для текущей цены, поскольку текущая цена проводит гораздо больше времени вдали от равновесной, чем вблизи нее. Это наводит на общие соображения о том, что если равновесие на рынке акций и существует, то оно является неустойчивым и динамическим.
3. Существуют три состояния на рынке (в принципе, наверное и больше, но явно и качественно выделяемых пока обнаруживается именно три).
Во-первых, ситуации в которых равновесная цена остается почти постоянной и текущая цена колеблется в нешироком диапазоне вокруг нее. Такие состояния можно определить как локальное равновесие на рынке.
Во-вторых, наиболее часто встречающиеся ситуации – это ситуации плавного изменения равновесной цены. Обычно это трендовые ситуации на графике текущей цены и они соответствуют процессу перехода цен к новому состоянию локального равновесия под действием рыночных новостей.
И, наконец, в третьих на рынке бывают крайне интересные ситуации, которые заключаются в том, что равновесная цена еще остается неизменной, а текущая цена достаточно сильно отклоняется от равновесной. Такие ситуации можно сопоставить с состоянием «фазового перехода» рынка от локального равновесия к тренду. Любопытно, что из теории фазовых переходов следует довольно однозначный вывод – если фазвый переход на рынке произошел, то возвращение цены к состоянию, откуда он начинался является крайне маловероятным событием. Это совпадает с моей трейдерской интуицией: после резких отклонений цен от более-менее сформированных торговых уровней быстрого возврата к ним практически никогда не происходит. Цена сначала «утаптывает» новые уровни и только потом может либо так же скачком (опять же фазовым переходом), либо медленно (плавным трендом) вернуться к исходной точке.
Три типа описанных ситуаций показаны на рисунке ниже:

Такое разделение состояний в зависимости от динамики равновесной цены позволяет строить новые торговые стратегии. Самый простой вариант стратегии – игра в трендах, где, очевидно, позиции должны заниматься по направлению изменения равновесной цены. Стратегии торговли в состояниях равновесия являются более сложными. С одной стороны логично определять статистический коридор колебаний вокруг равновесия и занимать от его границ позиции на возврат к равновесию. Однако здесь возникает риск попасть в ситуацию «фазового перехода». Но при этом само наличие «фазовых переходов» позволяет поставить задачу прогноза следующим образом: при данном отклонении текущей цены от равновесной что более вероятно – возврат текущей цены к равновесной или же начало процесса смещения равновесия в сторону отклонения текущей цены? Существуют ли факторы, позволяющие дать более точный ответ на данный вопрос? Вот этой задачкой, уважаемый Pereat, я и занимаюсь на досуге в последнее время. Т.е. поиском «объективных» уровней равновесия на разных масштабах, решением задачи прогноза движения цены и равновесия в состоянии «фазового перехода». А так же моделями движения цен в условиях существования большого количества уровней равновесия на разных горизонтах.
Автор Mikola
Первая – это, естественно, т.н. «справедливая цена» акций, вычисляемая из фундаментальных показателей (в первую очередь, потока будущих платежей). Если все вычисляют эту цену одинаково, то она и является равновесием, которое должно устанавливаться на рынке после появления новых фундаментальных данных. На практике же, оказывается, что различия в методах вычисления и конкретных параметрах (например, стоимости денег, или прогнозах потоков платежей) приводят к тому, что оценки, приводимых разными, безусловно, авторитетными аналитиками, могут отличаться в два раза. Впрочем, это было вполне приемлемо с точки зрения соответствия теории наблюдениям, если бы реальная цена большую часть времени проводила бы в коридоре, обозначенном аналитиками и/или колебалась возле консенсуса. В реальности мы видим совсем иное поведение – цена практически всегда находится очень далеко от консенус-прогноза и очень часто даже не попадает в коридор, определяемых фундаментальными оценками. Более того, внимательный анализ показывает, что примерно в половине случаев изменение фундаментальных прогнозов происходит после резких изменений цены (а не наоборот, как должно быть согласно теории).
Вторая парадигма объявляет равновесием текущую цену, ссылаясь на изобретенную еще Доу формулу: «цена учитывает все». При этом фундаментальная информация оказывается далеко не «всем», чем и объясняется сильное отклонение текущей цены от фундаментальной. В текущей цене с точки зрения сторонников этой парадигмы не менее важную роль играют настроения, слухи и ожидания на их основанные, которые и вносят в итоге весомый довесок в положение равновесия. Основная претензия к этой парадигме очевидна: можно ли считать равновесием нечто, что может изменяться столь быстро и столь же непредсказуемо, как цена акций?
Так существует ли равновесие на рынке? Можно ли найти какую-то здравую величину между практически никогда не достижимой фундаментальной ценой и слишком непредсказуемой текущей? Оказывается, можно. Для этого проведем забавный мысленный эксперимент. Представим себе много участников рынка, которым в начале игры раздали деньги и акции (все акции одинаковые). Кому-то только деньги, кому-то только акции, кому-то акции и деньги в разных пропорциях. Далее запустили обычный аукционный процесс торговли, обеспечили поток новостей на рынок и поставили целью участников заработать как можно больше денег к моменту «Х», который, допустим, заранее неизвестен. Когда на этом «рынке» установится нормальный торговый режим, объявим час «Х», после которого торги будут прекращены навсегда Портфель каждого участника будет оценен по последней цене торгов. Тем, кто закончит торги с суммой портфеля больше начальной будет выплачен весь полученный доход за счет тех, чьи портфели будут иметь оценку портфеля ниже начальной (понятно, что в такой замкнутой системе сумма проигрышей и выигрышей окажется одинаковой). Можно ли предсказать на какой цене закроется рынок в час «Х»? Оказывается, можно!
Проделаем несколько странных на первый взгляд процедур. Во-первых отсортируем все сделки, прошедшие на рынке по возрастанию от самой низкой к самой высокой. Во-вторых, просуммируем объемы сделок нарастающим итогом начиная с самой низкой цены. В третьих, просуммируем объемы сделок нарастающим итогом начиная с самой высокой цены. В результате мы получим две кривых. Одна будет увеличиваться при росте цены, вторая, наоборот уменьшаться при росте цены:

Рисунок получен по тиковым данных торгов акциями ОАО «Газпром» 22.08.11 с 10.30 до 16.00
Что будет происходить на нашем модельном рынке с момента объявления часа «Х»? Все, купившие акции ниже текущей цены будут стараться продать их, чтобы зафиксировать прибыль, а все продавшие акции выше текущей цены будут стараться купить акции, чтобы тоже зафиксировать имеющуюся прибыль. Соответственно две полученных выше кривых можно будет трактовать как кривую предложения акций (суммарный объем акций, купленный ниже текущей цены, будет выставляться на продажу для фиксации прибыли) и кривую спроса на акции (суммарный объем акций, проданных выше текущей цены, будет выставляться на покупку для фиксации прибыли). В экономике хорошо известна цена, к которой в итоге сойдутся торги – она будет определяться точкой пересечения кривых спроса и предложения. В приведенном на рисунке примере это будет цена около 168 рублей.
Итак, на модельном рынке, где известна дата окончания торгов можно определить цену к которой в итоге сойдется торги и в этом смысле такую цену можно считать равновесной (т.е. ценой к которой будет стремиться рынок в отсутствие новостей). Любопытно, что эта цена будет зависеть от траектории торгов и распределения объемов.
Имеет ли отношение рассчитанная таким образом равновесная цена к поведению реального рынка? Отдельные, рассчитанные описанным выше образом, цены на разных горизонтах я называю «локально равновесными» или просто «равновесными», а их набор «модернизированной планитерией» и занимаюсь по мере появления времени исследованием свойств этих цен или «уровней». Что понятно на текущий момент. Начнем со свойств одной равновесной цены, рассчитанной по произвольному фиксированному интервалу. На текущий момент понятно, что:
1. Равновесная цена является достаточно медленно изменяющейся функцией по сравнению с текущей ценой.
2. Равновесная цена является областью «отталкивания» для текущей цены, поскольку текущая цена проводит гораздо больше времени вдали от равновесной, чем вблизи нее. Это наводит на общие соображения о том, что если равновесие на рынке акций и существует, то оно является неустойчивым и динамическим.
3. Существуют три состояния на рынке (в принципе, наверное и больше, но явно и качественно выделяемых пока обнаруживается именно три).
Во-первых, ситуации в которых равновесная цена остается почти постоянной и текущая цена колеблется в нешироком диапазоне вокруг нее. Такие состояния можно определить как локальное равновесие на рынке.
Во-вторых, наиболее часто встречающиеся ситуации – это ситуации плавного изменения равновесной цены. Обычно это трендовые ситуации на графике текущей цены и они соответствуют процессу перехода цен к новому состоянию локального равновесия под действием рыночных новостей.
И, наконец, в третьих на рынке бывают крайне интересные ситуации, которые заключаются в том, что равновесная цена еще остается неизменной, а текущая цена достаточно сильно отклоняется от равновесной. Такие ситуации можно сопоставить с состоянием «фазового перехода» рынка от локального равновесия к тренду. Любопытно, что из теории фазовых переходов следует довольно однозначный вывод – если фазвый переход на рынке произошел, то возвращение цены к состоянию, откуда он начинался является крайне маловероятным событием. Это совпадает с моей трейдерской интуицией: после резких отклонений цен от более-менее сформированных торговых уровней быстрого возврата к ним практически никогда не происходит. Цена сначала «утаптывает» новые уровни и только потом может либо так же скачком (опять же фазовым переходом), либо медленно (плавным трендом) вернуться к исходной точке.
Три типа описанных ситуаций показаны на рисунке ниже:

Такое разделение состояний в зависимости от динамики равновесной цены позволяет строить новые торговые стратегии. Самый простой вариант стратегии – игра в трендах, где, очевидно, позиции должны заниматься по направлению изменения равновесной цены. Стратегии торговли в состояниях равновесия являются более сложными. С одной стороны логично определять статистический коридор колебаний вокруг равновесия и занимать от его границ позиции на возврат к равновесию. Однако здесь возникает риск попасть в ситуацию «фазового перехода». Но при этом само наличие «фазовых переходов» позволяет поставить задачу прогноза следующим образом: при данном отклонении текущей цены от равновесной что более вероятно – возврат текущей цены к равновесной или же начало процесса смещения равновесия в сторону отклонения текущей цены? Существуют ли факторы, позволяющие дать более точный ответ на данный вопрос? Вот этой задачкой, уважаемый Pereat, я и занимаюсь на досуге в последнее время. Т.е. поиском «объективных» уровней равновесия на разных масштабах, решением задачи прогноза движения цены и равновесия в состоянии «фазового перехода». А так же моделями движения цен в условиях существования большого количества уровней равновесия на разных горизонтах.
Автор Mikola
4 Комментария
 mrTrader22 декабря 2011, 20:17Александр! Супер!++1
mrTrader22 декабря 2011, 20:17Александр! Супер!++1 sanches22 декабря 2011, 20:21не по курсу, график чего изображён???0
sanches22 декабря 2011, 20:21не по курсу, график чего изображён???0 Андрей Скрипко22 декабря 2011, 22:56А избранное, гранд мерси!0
Андрей Скрипко22 декабря 2011, 22:56А избранное, гранд мерси!0
Читайте на SMART-LAB:

Итоги Smart-Lab & Cbonds PRO облигации 2026
Итоги Smart-Lab & Cbonds PRO облигации 2026
28 февраля прошла конференция по вопросам облигационного рынка Smart-Lab & Cbonds PRO облигации 2026 , в рамках которой на сессии...
20:59

Как я шортил нефтянку и индекс на фоне войны в Иране и сколько на этом потерял: работа над ошибками
💥 Как я шортил нефтянку и индекс на фоне войны в Иране и сколько на этом потерял: работа над ошибками
Бывает, находишь схему, с которой уверенно зарабатываешь на рынке. Но потом...
17:30











