Альтернативный расчет стоимости опционов.
В прошлый раз мы определили стоимость опциона на деньгах. smart-lab.ru/blog/248456.php Теперь попробуем рассчитать стоимость опциона вне денег. За базу отсчета возьмем полученную ранее цену опциона на деньгах и обозначим ее буквой W. Это вроде как, некий параметр включающий в себя вегу и тэту (для любителей стандартного представления).
Теперь, посмотрим на изменение цены базового актива немного под другим углом. Представим, что потенциальная возможность изменения цены из точки, в которой она находится сейчас в другую точку, (волатильность) есть некая мощность излучения заложенная в данной точке. То есть, волатильность мы представим как мощность излучателя возмущений некоего «финансового пространства».
И цену опциона на деньгах, мы можем представить как результат воздействия этого «излучателя» на опционное пространство данной серии опционов в нулевой точке ( в эпицентре).
То есть W (цена на центральном страйке) – это мощность источника излучения «волатильности» в опционном пространстве. А цены на страйках вне денег – это значения мощности сигнала на расстоянии от источника излучения. И чем дальше страйк, тем слабее сигнал.
Исходя из выше приведенной гипотезы, мы можем попробовать приложить закономерности физического мира к нашему виртуальному миру опционов.
Распространение сигнала в физическом мире характеризуется тем, что сигнал затухает (теряет мощность) пропорционально квадрату расстояния от источника сигнала. Общая формула выглядит так:
Р1/Р0 = КК /(R^2), или Р1 = Р0 * КК /(R^2)
Где
Р0 – мощность излучателя
R – расстояние до излучателя
Р1 – мощность на расстоянии R
КК – набор коэффициентов характерный для конкретного излучения в конкретной среде.
Рассмотрим наш случай. Для удобства возьмем источник излучения единичной мощности W=1. В упрощенном варианте а опциона вне денег (Wi), будет равна:
Wi=1/(R^2), где R – расстояние от цены страйка до цены базового актива.
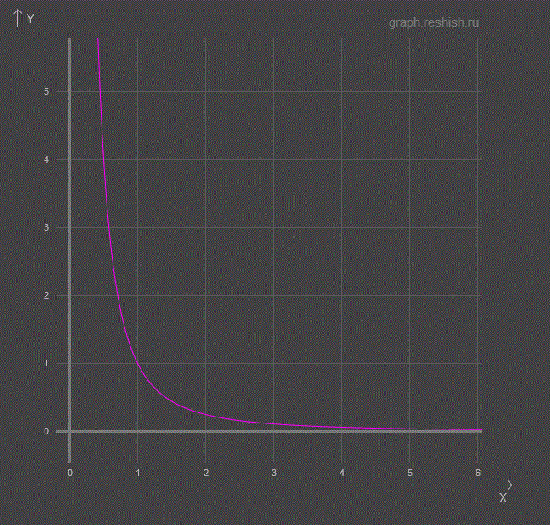
Прикинем как это будет выглядеть на графике:
Получилось не совсем то, что хотелось. При значениях R<1 сигнал оказывается больше 1 !!!
При консультации со знающими людьми выяснилось:
- Сигналы распространяются пропорционально квадрату расстояния
- Формула, по которой всё это считается некорректна на очень малых расстояниях.
Попробуем поправить мировую науку и исключить возможность знаменателю в формуле быть меньше 1.
Wi=1/(R^2 + 1)
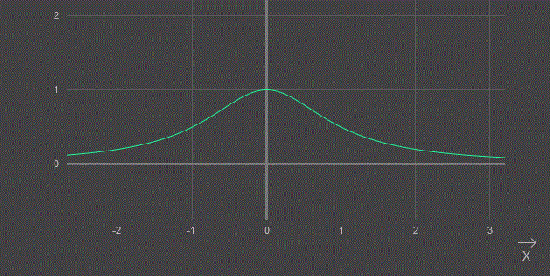
Смотрим на график:
Получилась очень знакомая картинка для опционных трейдеров.
Но этот график для сигнала W=1. Нам надо его масштабировать для любых значений W.
Усложняем немного формулу:
Wi=W/((R/W)^2 + 1),
где
R – расстояние от цены страйка до цены базового актива.
W – цена опциона на деньгах.
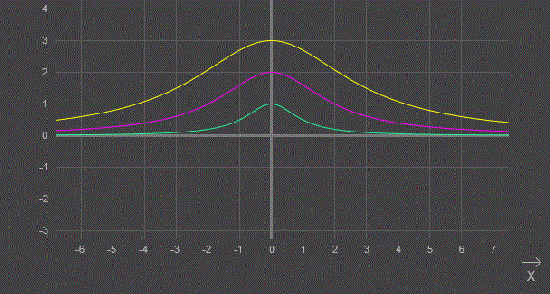
Строим графики при разных значениях W
Приложив данную формулу к рынку и сопоставив ее с формулой Б-Ш получаем следующие результаты:
1. Формула вполне пригодна для описания рынка
2. Формула имеет отличие от Б-Ш, но не критические.
3. Дальние страйки имеют толстые «хвосты».
4. Используя формулу мы получаем форму «улыбки», как с поднятыми концами, так и с опущенными или прямыми (в зависимости от состояния рынка).
Это верно только для 3x мерной среды.
Ценовая шкала, как известно, имеет одно измерение. А в одномерной среде сигнал вообще не затухает. Например, в проводе(сопротивление среды не в счёт).
А так подход интересный. Но ошибка серьёзная
Но факт затухания воздействия от расстояния присутствует. :))) и самая близкая закономерность оказалась квадратичная.
А что значит «находка»? :)) Шел, шел и нашел на ровном месте?
Или методом подбора, что попало, лишь бы совпало? :))))
Если «находку» нашли Вы — то это открытие)).
Для любого открытия нужен практический, подтверждающий фундамент… это я к тому, что было бы не плохо — сравнить Ваш подход и классическую теорию на временном промежутке. Какие расхождения при одинаковых условиях?
К примеру — как лучше считать доходность — как обычно или через логарифм? Второй вариант сжимает доходность во времени, убирая тяжелые хвосты в статистике.
А в Вашем варианте как? Какие изменения?
Хотя, я продолжу потом эту тему, по-немногу, в свободное время :))
Сам провожу исследования (в своей области — формирование портфелей) — времени съедает очень много.