10 декабря 2014, 22:29
Анализ опционной позиции через распределение вероятностей
Возникла тут идея — как можно было бы оценивать позу без греков, модели Блэка-Шоулза (БШ) или более сложных моделей, требующих продвинутых познаний в математике. Все, что потребуется — это рыночное распределение вероятностей цен на экспу и анализ того, как меняются оценки позиции при определенных изменениях этого распределения. Реализовал эту идею, хотел бы поделиться результатами. Буду рад получить порцию критики или новых идей, ну и вообще обсудить.
Для примера решил рассмотреть позицию зигзаг:
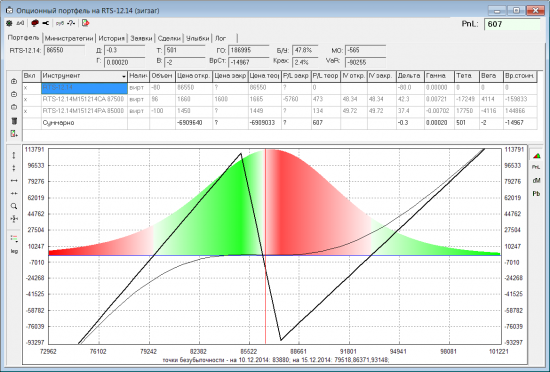
Но это все статичная оценка портфеля. А что если менять отдельные моменты у распределения и смотреть, как при этом изменяется оценка позиции? Чтобы поиграться с этим — реализовал изменение первых четырех моментов у рыночного распределения. Почему именно первых четырех? Просто пока экспериментировал с моделированием улыбки, пришел к таким выводам (возможно ошибочным):
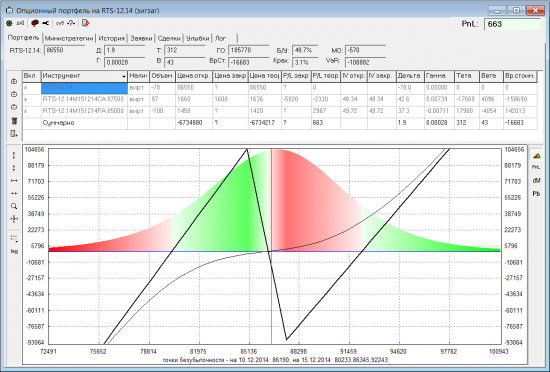
Отличие от исходной позы минимальное, но все же. Возможно, если бы времени до экспы было больше или поза была бы посложнее, то различие было бы больше.
Теперь рассмотрим, что будет с оценкой позы, если менять третий момент распределения (его асимметрию). Вот такой получается график от M3:
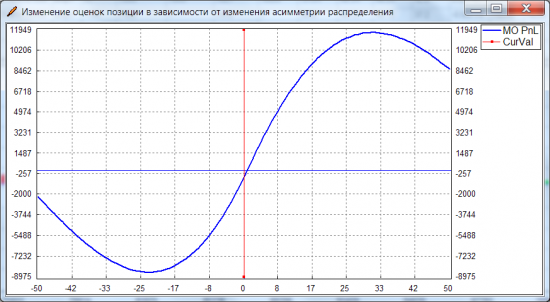
В динамике это выглядит так. Похоже на волшебство: БА и IV ATM стоит на месте, а PnL позы существенно меняется.
Получается, что торговля таким зигзагом — это направленная торговля асимметрией распределения. Будет приносить прибыль, если асимметрия будет уменьшаться (распределение будет стремиться к симметричному), и минусить, если асимметрия будет увеличиваться.
Вот такой анализ по зигзагу получился. Используя только рыночное распределение (и не используя БШ), мы смогли занейтралить позу по первым двум моментам, и увидеть какой у нее риск по третьему. Интересно мнение тех, кто на практике торговал этой позицией — насколько результаты такого анализа отвечают действительности?
И как вообще идея — раскладывать основные риски позиции на первые четыре момента распределения и анализировать их по-отдельности? Или все это «чушь собачья»? :)
Для примера решил рассмотреть позицию зигзаг:
Пропорции в этой позе подобрал так, чтобы дельта и вега (по БШ) были равны нулю. Т.е. с точки зрения БШ, позиция — нейтральная.
Имея распределение вероятностей, мы можем посчитать различные оценки нашей опционной позиции, такие как:
- вероятность безубытка на экспу (площадь под зелеными участками распределения)
- вероятность краха (если задать размер недопустимых потерь для портфеля)
- матожидание PnL
- текущий PnL
- VaR (для заданного доверительного уровня)
Но это все статичная оценка портфеля. А что если менять отдельные моменты у распределения и смотреть, как при этом изменяется оценка позиции? Чтобы поиграться с этим — реализовал изменение первых четырех моментов у рыночного распределения. Почему именно первых четырех? Просто пока экспериментировал с моделированием улыбки, пришел к таким выводам (возможно ошибочным):
- Первый момент (матожидание) распределения равен текущей цене БА.
- Второй момент (дисперсия) зависит в основном от текущей волы БА, но еще и от средней волы и скорости возвращения к ней.
- Третий момент (асимметрия) — от корреляции БА и волы, а также, от разной вероятности/силы гэпов вниз и наверх.
- Четвертый момент (эксцесс, толстые хвосты) — от VolOfVol, и от вероятности/сигмы гэпов и взлета волы после них, т.е. в какой-то мере это текущий «страх» на рынке.
Отличие от исходной позы минимальное, но все же. Возможно, если бы времени до экспы было больше или поза была бы посложнее, то различие было бы больше.
Теперь рассмотрим, что будет с оценкой позы, если менять третий момент распределения (его асимметрию). Вот такой получается график от M3:
В динамике это выглядит так. Похоже на волшебство: БА и IV ATM стоит на месте, а PnL позы существенно меняется.
Получается, что торговля таким зигзагом — это направленная торговля асимметрией распределения. Будет приносить прибыль, если асимметрия будет уменьшаться (распределение будет стремиться к симметричному), и минусить, если асимметрия будет увеличиваться.
Вот такой анализ по зигзагу получился. Используя только рыночное распределение (и не используя БШ), мы смогли занейтралить позу по первым двум моментам, и увидеть какой у нее риск по третьему. Интересно мнение тех, кто на практике торговал этой позицией — насколько результаты такого анализа отвечают действительности?
И как вообще идея — раскладывать основные риски позиции на первые четыре момента распределения и анализировать их по-отдельности? Или все это «чушь собачья»? :)
URL
0.027
В 2023 не было дивидендов
Удвойте свой доход с ВТБ!
Реклама
Откройте вклад в ВТБ со ставкой 27% и удвойте доход по программе долгосрочных сбережений.
может к концу года 30 увидим?
МИД Израиля и ЦАХАЛ подтвердили убийство главы ХАМАС Яхьи Синвара в секторе Газа
И кстати по цене акции в 0,4р. Заплатить дивы 0,1р. Цена улетит на 0,3р. Как вы думаете, как быстро закроется дивгэп при такой цене? Или есть другой вариант, разбить выплату див по пол года, что бы не...
Школа Свободных Наук,
Для участия в таких программах нужны свои деньги на счёте, про какие заемные и маржин колы идет речь?
bepybo, Посмотрел, замечательное видео!
Aboldet, наглядная иллюстрация теоремы Тарана, как перемога превращается в зраду
Главные потери этого года для пропаганды Solidcore и ММВБ:
После ряда вскрытий нашими силами косяков эмитента и Мосбиржи:
16.10.2024
директору по связям с инвесторами Евгению Монахову сказ...
Vic, для ориентира, в отчете Газпром писал, плюс 100бп к ставке по займам — это минус 30млрд из прибыли до налогов.
Netflix, Inc. — Прибыль 9 мес 2024г: $6,843 млрд (+53% г/г)
Взяли цены на рынке, построили распределение. А дальше?
>Т.е. если посчитать по нему справедливые цены опционов, то они будут лежать между текущими бид-асками в стаканах
Зовите дядю Лёшу!
А если серьёзно — «Не умножай сущностей без нужды».
См. smart-lab.ru/blog/fun/199468.php
Фэнкс!
IV ATM ~ M2
наклон улыбки ~ M3
крутизна краев ~ M4
Когда увеличиваю M4, то улыбка начинает поднимать крылья. Когда уменьшаю — опускает крылья и постепенно превращается в прямую.
Вот только угол наклона улыбки (в точке текущей цены БА), если его никак не нормировать, ведь будет зависеть не только от асимметрии, но и от оставшегося времени до экспы, и от IV ATM, и общего изгиба улыбки. Т.е. фактически от всех трех моментов M2-4. Имхо, интереснее анализировать позицию, когда есть возможность независимо менять каждый фактор, от которого зависит PnL. Но это только предположение, может и неправ.
вот поэтому я раньше шарахался от опционов как от огня, мой стаж на рынке 7 лет, опционами торгую 1.5 года
здесь нужно проще работать ...
что ВАМ дает этот анализ, ну в лучшем случае 10 — 20% годовых, а смысл?
лучше работать по тренду опциками, у меня доход за 8 месяцев под +800% и я честно говоря много прозевал и упустил, я пока только учусь максимально выжимать с поз
ГОСПОДА РАБОТАЙТЕ ПО ТРЕНДУ ОПЦИОНАМИ, там все очень просто
Эта штука называется рискревёрсал :)
> Интересно мнение тех, кто на практике торговал
> этой позицией — насколько результаты такого
> анализа отвечают действительности?
Чтобы занулить вклад моментов ниже k-го, достаточно в портфеля из k-1 страйка + фьюча. «Стандарт» для торговли 3-им моментом это как раз и есть зигзаг, а для торговли 4-ым — баттерфляй.
> И как вообще идея — раскладывать основные риски
> позиции на первые четыре момента распределения и
> анализировать их по-отдельности? Или все это
> «чушь собачья»? :)
Могу посоветовать визуализировать вот так:
ось X — M1, ось Y — M2, PNL — цвет точки
Если есть какая-то модель взаимоотношения моментов — поверх графика можно нанести линии уровня совместной плотности M1, M2
Такой график доступно ориентирует, к сожалению не могу приложить картинку, так как считалку-рисовалку забросил в 2009м.
PS: А вы бываете на каких-нибудь не очень массовых оффлайн мероприятиях? Вроде бы иногда происходят небольшие опционные тусовки, но я мало кого знаю и меня туда никто не зовёт, было бы интересно поговорить.
smart-lab.ru/blog/207002.php
спс, перевариваю картинку ))
Чтобы занулить вклад моментов ниже k-го, достаточно...
Это научный факт или просто по опыту торговли?
«Стандарт» для торговли 3-им моментом...
Т.е. действительно бывает направленная торговля только каким-то конкретным моментом (а остальные при этом занейтралены)? А бывает, что торгуют выше чем четвертым моментом? :)
Могу посоветовать визуализировать вот так...
О, спасибо, кажется это будет интересно :) А что такое линии уровня совместной плотности? Это что-то вроде канала, внутри которого будут наиболее вероятные пары (M1, M2)?
Насчет оффлайн тусовок — таких не знаю. Есть группа в FB, посвященная обсуждению лекций Кирилла Ильинского. Там высокий уровень обсуждения опционов. Мало что понимаю, но все равно интересно :) Сейчас скину в личку ссылку на нее.
>> Чтобы занулить вклад моментов ниже k-го, достаточно...
> Это научный факт или просто по опыту торговли?
Это «почти-наверное-факт» для бездивидендного случая. В том смысле что, возможно для какого-то особого распределения и есть какие-то особые наборы из k-1 страйка где не получится, но в общем случае проблем быть не должно.
>> «Стандарт» для торговли 3-им моментом...
> Т.е. действительно бывает направленная
> торговля только каким-то конкретным моментом
> (а остальные при этом занейтралены)?
Я подумал — у «стандартных» рискревёрсала и бабочки всё же зануления по моментам нет, там выравнивание по количеству, вы и сами видели, что разница именно что «не большая, но всё же ...». Стандартный рискревёрсал это почти чистый третий момент, стандартный баттерфляй — почти чистый четвёртый.
В индустрии как-то более принято всё же считать/нейтралить/брать_направленно греков (дельту, вегу, ванноволгу) в терминах волатильностей, а не моментов. Но мне кажется это просто, чтобы люди говорили на одном языке.
> А что такое линии уровня совместной плотности?
> Это что-то вроде канала, внутри которого будут
> наиболее вероятные пары (M1, M2)?
Да, именно оно, что-то типа эллипсов на самом деле, не каналы. Более формально, если есть функция f(x, y) — то линия уровня C — это решения уравнения f(x, y) = C, f(x, y) — в данном случае плотность распределения. Просто для общей картины добавлю, что линии уровня плотности распределения очерчивают не «наиболее вероятные области», а «наиболее правдоподобные».
> Сейчас скину в личку ссылку на нее.
спасибо
Приглашение отправил.
Сделал визуализацию матрицы. Вот, например, как выглядит для купленного стрэддла на центре, с дельтой по БШ=0:
Посередине квадратик соответствует текущему распределению, без смещений (M1=0, M2=0). Видно, что любое смещение М1 (т.е. движение БА) приносит прибыль, и чем дальше смещение, тем больше PnL. Падение M2 (или IV ATM, или временной распад — он тоже уменьшает M2) приносит убыток, но только если M1 сильно не меняется.
Т.е. картинка вроде соответствует истине. Непонятно только — какую из нее пользу можно извлечь.
Сделал сразу до кучи, чтобы и другие пары моментов можно было смотреть. Но пока ничего интересного не обнаружил. Вот, например, картинка для зигзага, изменение PnL в зависимости от (M1,M3). Хотя PnL зависит от M3, но этот вклад меркнет на фоне зависимости от M1.
мне кажется, где-то есть ошибка, верхние левый и правый углы должны быть по-зеленее, чем оба нижние, и напрашивается сделать zoom-in по M1 и zoom-out по M2
хорошо, что вы сделали картинку — под линииями уровня я имел ввиду примерно вот это:
само совместное распределение я пробовал честно монтекарлить, по модели аля-хестон, но с двумя волатильностями:
— sigma — которая в уравнении на dPrice
— vix — это собственно vix, т.е. iv воображаемого портфеля 30-дневных опционов
и поверх этого ещё модель iv(days_to_expiration) = iv(sigma, vix, days_to_expiration)
но оказалось слишком много параметров, поэтому в продакшн пошли «эллипсы» по эмпирическим корреляциям dM1 и dM2 (всего один коэффициент)
линии уровня пригодятся для наглядного понимания, того, что левый нижний и правый верхний угол — не основное.
и нужны они уже на фазе asset alocation, когда всаёт вопрос, «а что же лучше — +50р на 110м коле или +100р на 90м путе?»
видимо дело в малой времянке, которая осталась в RTS-12.14. Построил для январской серии RTS-3.15, зуммировал, вот какая картинка получилась. Красный холмик несимметричен, наверное потому что фьюч на 76280, а страйк стрэддла 75000. В остальном — вроде все правильно показывает?
Спасибо за картинку с линиями уровней — теперь лучше стал понимать. Правильно ли понимаю, что мне на истории нужно построить облачко точек (dM1, dM2), и отсекая выбросы 5%, 20%, 50% — получу вот такие три области 95%, 80% и 50%? Как построить такие облачка — понимаю, но вот как запомнить их границы, чтобы можно было в любой момент нанести на матрицу — что-то затрудняюсь… Или можно просто посчитать корреляцию между dM1 и dM2, получить одно число, и потом по какой-то формуле получать «эллипсы» для заданного доверительного интервала?
> В остальном — вроде все правильно показывает?
Выглядит правдоподобно :)
> Правильно ли понимаю, что мне на истории
> нужно построить облачко точек (dM1, dM2),
Да, но надо быть аккуратным — где цена, где процент, где логарифм, оно очень чувствительно к единицам измерения. Я вот что имею ввиду: опционы за 10р на актив стоящий 1000р должны восприниматься эквивалентно опционам стоящим 1р на актив стоящий 100р, хотя M1 и M2 у них разные.
> получить одно число, и потом по какой-то
> формуле получать «эллипсы» для заданного
> доверительного интервала?
Я этим путём пошёл, тут большой вопрос как распределён M2, я наивно положил, что ln(M2) распределён нормально, более честно — смотреть в сторону хи-квадрата, но это тоже не оно.
Далее рассуждения в координатах dln(M1) и dln(M2) как для двух коррелированых нормально распределённых.
Чем ненормальнее высшие моменты — тем хуже работают «наивные эллипсы».
Может быть стоит и не отвлекаться на линии уровня, они когда-нибудь всё равно возникнут как следствие, там и промонтекарлите.
Напишите лучше, что вы думаете делать если у вас есть «достаточно много исторических данных»
> Да, но надо быть аккуратным
Спасибо. Так понимаю — лучше рассматривать логарифм? Т.е. рассматривать такие приращения dM = Ln(M(i+1)/M(i)) и именно для таких приращений строить облака/распределение/считать корреляцию между разными моментами?
А какой таймфрейм (TF) посоветуете? История биржевых улыбок на RTS поминутная, но TF=1мин наверное не подойдет для выявления зависимостей. Ведь когда БА сильно изменяется, вряд ли биржевая улыбка тут же это учитывает и изменяется. Пока думаю взять TF=5мин, но может неправ и нужно больше?
> тут большой вопрос как распределён M2
Конкретно M2 еще не смотрел, но строил распределение для приращений IV на центре (т.е. значение на улыбке IV в точке текущего значения фьюча). Приращения считал как (CurIV-PrevIV)/PrevIV (это процент?) Картинка получалась такая. Черная линия — это наложил нормальное распределение с такой же сигмой. Видно, что отличие от нормального очень большое. Поскольку M2 тесно связан с таким IV, то наверное M2 будет примерно также распределен.
> что вы думаете делать
Собираюсь посмотреть какие попарные зависимости есть между M1/M2/M3/M4. Только, наверное, не чистые M3 и M4 брать, а как-то нормировать на сигму. Наверное так: M3/sigma^3 и M4/sigma^4.
Она очевидно должна быть из какого-то достаточно богатого семейства, чтобы имелась возможность независимо регулировать каждый из моментов...
Первые два момента у такого распределения менять легко — просто параллельный сдвиг и сжатие/растяжение. А вот M3/M4 — действительно проблема. Меняю их путем подмешивания нормального распределения к физическому, с некоторыми мю/сигмой/весом. Потом перенормирую, чтобы вернуть M1 и M2 к нужным значениям. Для приблизительной оценки, как будет в динамике меняться оценка позы при изменении M3/M4 — имхо, сойдет. Но если посоветуете, как более точно менять эти моменты — буду благодарен.
Хочется познать глубину кроличьей норы… А как Вы извлекаете «подразумеваемое IV»? Это ведь тоже надо суметь сделать грамотно, учитывая ограниченный набор страйков. Может пойти искуственный «звон» по распределению…
Не совсем понял про «подразумеваемое IV». Беру биржевую формулу с параметрами ABCDES, и подбираю эти параметры так, чтобы полученная улыбка выдавала теор.цены, которые бы наилучшим образом лежали между текущими бид-асками в стаканах. А потом уже из такой подобранной улыбки вычисляю подразумеваемое распределение.