02 ноября 2014, 17:29
HELP! Уравнение плотности нормального распределения
Помогите, кто чем может! Вторые сутки не сплю!
Возникла необходимость расчитывать теор. цену опциона в WealthLab.
Не могу правильно посчитать плотность стандартного нормального распределения для d1.
Напомню теорию, чтобы было понятнее в чем проблема
Цена опциона:
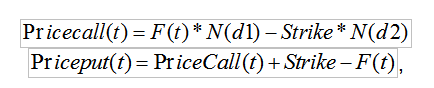
d1:

Считаем d1, теперь нужно сделать N(d1), т.е. плотность стандартного нормального распределения для d1. Именно тут я на ровном месте выпал в аут.
Формула простая
 вместо z, соответственно d1.
вместо z, соответственно d1.
В екслеле эта формула задана оператором НОРМСТРАСП(), с ним у меня все получается и цена опциона получается как на РТС.
Но мне нужно закодить эту формулу в ручную в WealthLab и никак не получается правильно посчитать, оператор НОРМСТРАСП() выдает разные значения с тем что я считаю вручную. Вроде формула простая, не могу понять в чем ошибка.
НАПРИМЕР:
В ексель для х=1 значение НОРМСТРАСП(1)= 0,841344746
Теперь, что получается у меня (разложу по частям чтоб было понятно что я делаю):
1/корень 2*пи = 0,39894228
e = 2,718281828
-x*x/2 = -1*1/2= -0,5
exp(-x*x/2) = 2,718281828 в степени -0,5 = 0,60653066
теперь 0,39894228*0,60653066= 0,241970725
в чем проблема-то? Что не так? Не могу понять, что я не так делаю.
ПОМОГИТЕ!
РS
Ребята, какие же Вы молодцы! Большое всем спасибо, вставили мне мозг в правильное место.
SmartLab самый умный сайт в мире!
Возникла необходимость расчитывать теор. цену опциона в WealthLab.
Не могу правильно посчитать плотность стандартного нормального распределения для d1.
Напомню теорию, чтобы было понятнее в чем проблема
Цена опциона:
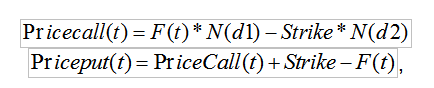
d1:

Считаем d1, теперь нужно сделать N(d1), т.е. плотность стандартного нормального распределения для d1. Именно тут я на ровном месте выпал в аут.
Формула простая
 вместо z, соответственно d1.
вместо z, соответственно d1.В екслеле эта формула задана оператором НОРМСТРАСП(), с ним у меня все получается и цена опциона получается как на РТС.
Но мне нужно закодить эту формулу в ручную в WealthLab и никак не получается правильно посчитать, оператор НОРМСТРАСП() выдает разные значения с тем что я считаю вручную. Вроде формула простая, не могу понять в чем ошибка.
НАПРИМЕР:
В ексель для х=1 значение НОРМСТРАСП(1)= 0,841344746
Теперь, что получается у меня (разложу по частям чтоб было понятно что я делаю):
1/корень 2*пи = 0,39894228
e = 2,718281828
-x*x/2 = -1*1/2= -0,5
exp(-x*x/2) = 2,718281828 в степени -0,5 = 0,60653066
теперь 0,39894228*0,60653066= 0,241970725
в чем проблема-то? Что не так? Не могу понять, что я не так делаю.
ПОМОГИТЕ!
РS
Ребята, какие же Вы молодцы! Большое всем спасибо, вставили мне мозг в правильное место.
SmartLab самый умный сайт в мире!
Читайте на SMART-LAB:
Технологии как новый драйвер: ключевые идеи инвестиционного форума ВТБ «РОССИЯ ЗОВЕТ!»
🧮 Главный тренд 2026 года — стабилизация и технологический поворот
Руководитель департамента по работе с клиентами рыночных отраслей ВТБ Дмитрий Средин:
Снижение ключевой ставки...
20.02.2026
ВТБ обещал миноритариям обойтись без допэмиссии
Акции ВТБ в ходе торгов 20 февраля, проходивших на российском рынке в умеренном плюсе, вышли в лидеры роста, подорожав на 3,4%, до 88,42 руб.Менеджмент финансовой корпорации раскрыл параметры...
20.02.2026

ПКО «Вернём». Зачем облигации при масштабировании бизнеса?
В эфире PRObonds генеральный директор ПКО «Вернём» Павел Ивановский и финансовый директор Роман Гаммель. С ответами на вопросы о новом эмитенте облигаций, о регулировании коллекторского...
14:01

Россети Центр. Отчет об исполнении инвестпрограммы за Q4 2025г. Ожидаемо снизилась дивидендная база по РСБУ.
Компания Россети Центр опубликовала отчет об исполнении инвестпрограммы за Q4 2025г., где показаны финансовые показатели компании по РСБУ в 4 квартале (ну и понятно за целый год): 👉Выручка...
19.02.2026










Public Function d_1(ByVal F As Double, ByVal K As Double, ByVal T As Double, ByVal Sigma As Double) As Double
d_1 = (Log(F / K) + T * 0.5 * Sigma * Sigma) / (Sigma * Sqr(T))
End Function
Public Function nd_1(ByVal d1 As Double) As Double
nd_1 = Math.Exp(-1 * (d1 ^ 2) * 0.5) / Sqr(2 * PI)
End Function
Например вот такой (кусок на C#):
//------------------------------------------------------------
double N(double x)
{
double y = 0;
double ax, t, d, p;
if (x > 10)
y = 1;
else if (x < -10)
y = 0;
else
{
ax = Math.Sqrt(x * x);
t = 1 / (1 + 0.2316419 * ax);
d = 0.3989423 * Math.Exp(-0.5 * x * x);
p = d * t * ((((1.330274 * t — 1.821256) * t + 1.781478) * t — 0.3565638) * t + 0.3193815);
y = p;
if (x > 0)
{
y = 1 — p;
}
else
{
y = p;
}
}
return y;
}
Думаю разберетесь.