Сложность применения теории вероятности в торговле.

Тема теории вероятности не раз поднималась.
Хочу добавить от свои мысли на этот счёт.
Топик поднимает лишь одину из проблем, связанных
с теорией вероятности, а есть ещё и другие.
Сам использую распределения изменения цены. Т.е. рост или падение
не принципиально, главное что цена изменилась на определённое
число пунктов.
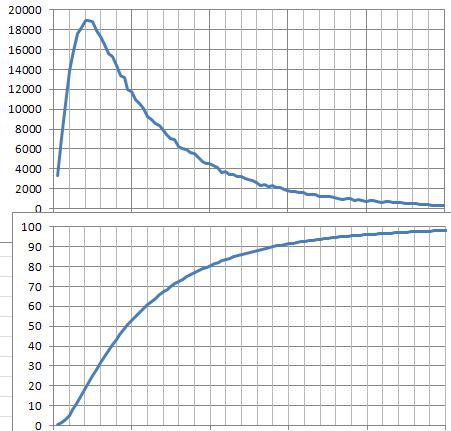
Для примера возьму распределение для 60 пунктов изменения цены
и соответствующую ему плотность распределения вероятности.




Для описания проблемы есть примерный график цены в консолидации.



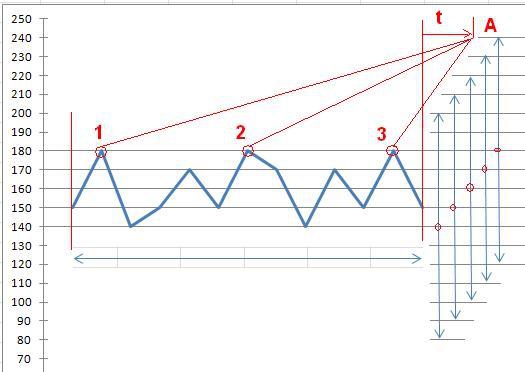
Ширина консолидации 40 пунктов цены, значит ни для одного уровня
цены внутри событие, что цена ушла на 60 пунктов в любую сторону
ещё не произошло. Для точек 1, 2 и 3 рост цены до уровня А будет
означать изменение на 60 пунктов. Однако для точки 1, как самой
дальней в консолидации, вероятность этого события составит
допустим 60% (как и вниз тоже 60%), для точки 2 30%, а для
точки 3 лишь 10% через время t. Важный ньюанс, потому что 10%
достижения уровня не означает, что 90% цена там не будет вообще.
Не будет через время t с 90% вероятности.
Несмотря на то, что достижение ценой уровня А — событие для всех
3-х точек, суммировать вероятности нельзя. Принять их равными
большей, или меньшей, или средней вероятности тоже нельзя.
Собственно в этом одна из сложностей. Мы в праве выбрать любую
стартовую точку и для всех выборов распределение справедливо.