Начинающий алготрейдер -- чем чаще сделки, тем хуже?..
С утра пораньше возникла мысль насчет сравнения стратегий с частыми и редкими сделками на чувствительность к издержкам.
Поставлю задачу так: если нужно добиться нетто (то есть с учетом издержек) доходности в R_net, какая должна быть брутто доходность R_gross?
Формулы для случая рекапитализации:


r — доходность одной сделки, s — издержки с одной сделки.
Из второй формулы выражаем r и подставляем в первую, получаем:

Чтобы исследовать эту зависимость, зафиксируем R_net = 50% (хочу 50% в год чистыми), s=0.2% (издержки с одной сделки), построим график от n:

Например:
При числе сделок 100 в год, нужен брутто в 100%
При числе сделок 300 в год, нужен брутто в 200%
При числе сделок 500 в год, нужен брутто в 350%
— чтобы достичь нетто в 50%.
Асимптотически при n->inf имеем:
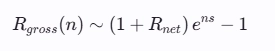
Гросс зависит экспоненциально от количества сделок!
Имеем два «парадоксальных» вывода:
— Частые стратегии менее выгодны, чем редкие
— В частых стратегиях лучше использовать фиксированную позицию, а не рекапитализацию.
Без рекапитализации формула выглядит так:

Конечно, это идеализированная модель: согласно ей, выгоднее всего сделать ровно одну сделку с заданной прибылью, тогда издержка будет минимальна; но заставляет задуматься, что, скорее всего, в каждой стратегии есть какой-то оптимум на количество сделок:
— При слишком маленьких n не отслеживается рыночная динамика
— При слишком больших n издержки съедают доходность.
И у меня есть ощущение, что для «классических» (не HFT) стратегий оптимум лежит скорее в часовых/дневных интервалах, а не в минутных.
Критикуйте!














чтоб гарантировать исполнение сделки в тестировщике надо выствить параметр сделка при пересечении цены а не просто при касании цены...
но опять же есть америка и тот же букинг 5000баксов за акцию при комиссе 0.35 цента
Зависимость от R_net обратная. Вот график при фиксированном gross=100%.
И ваше Rnet станет отрицательным. Соответственно, Rgross по экспоненте повалится к минус 1.
Недостаточно считать только по средним, нужно выбросы как-то учитывать и ограничивать.
Второй пост говорит о том, что при росте n неизбежно станет r<s для той же ТС.
svgr, ваше замечание очень просто обойти. Просто предположим, что r — это среднее геометрическое (а не арифметическое) за все сделки, тогда все формулы остаются точными.
Среднее геометрическое приближается к среднеарифметическому при уменьшении волатильности r.
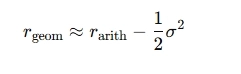
Второе замечание про рост n: оно говорит о том, что частотные стратегии еще хуже, чем эта идеальная модель, то есть основной вывод, что менее частотные стратегии лучше, сохраняется.