uralpro
Линейная регрессия с использованием фильтра Калмана
- 23 апреля 2015, 10:12
- |
Линейная регрессия часто используется для вычисления пропорции хеджирования в парном трейдинге. В идеальной ситуации коэффициенты этой регрессии — наклон линии регрессии и свободный член (пересечение) остаются всегда постоянными. Однако в реальности все, конечно, не так радужно, и значения этих параметров постоянно меняются во времени. Как правильно вычислять коэффициенты регрессии, чтобы избежать подгонки к текущей ситуации, рассматривается в статье "Online Linear Regression using a Kalman Filter". Для этой цели в данной публикации используется фильтр Калмана.
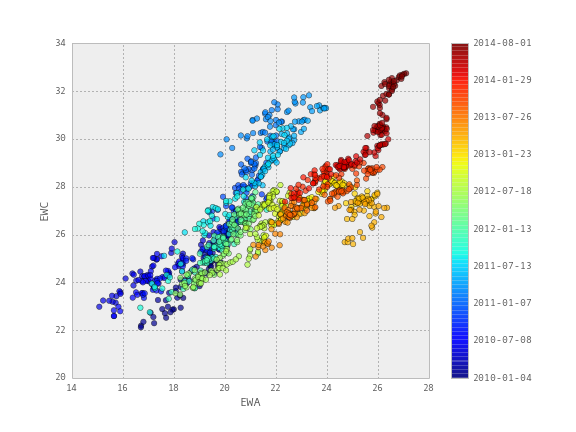
Для тестирования берутся исторические цены закрытия двух биржевых фондов ETF — австралийского EWA и канадского EWC с 2010 по 2014 год. Динамика цен этих фондов показывает взаимосвязь, что продемонстрировано на диаграмме рассеивания в заглавии поста. Однако по этому же графику видно, что эту взаимосвязь невозможно описать с помощью линейной регрессии с постоянными коэффициентами.
( Читать дальше )
- комментировать
- ★35
- Комментарии ( 12 )
Использование CART в предсказании направления рынка
- 21 апреля 2015, 10:19
- |
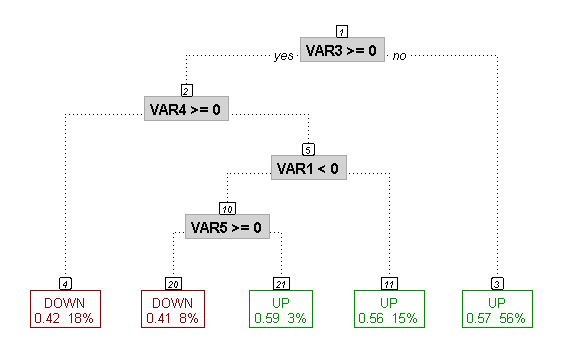
Интересный подход к предсказанию направления рынка рассмотрен в статье "Using CART for Stock Market Forecasting". Для того, чтобы предугадать движение цены на недельном отрезке используется техника под названием CART (Classification And Regression Trees) — построение классификационного графа (дерева) с целью предсказать значение целевой характеристики (цены) на основании набора объясняющих переменных. CART находит применение во многих областях науки и техники, но применим и в торговле, так как обладает набором свойств, хорошо подходящими для этой цели:
- может применяться при любом типе статистического распределения
- может применяться как для линейных, так и нелинейных зависимостей
- устойчив к событиям, выходящим за рамки статистических распределений
Для построения дерева автор использует библиотеку языка R, вычисляющую рекурсивное разделение (Recursive Partitioning) rpart.
( Читать дальше )
Модернизация стратегии robot_uralpro. Lead-lag relationship
- 16 апреля 2015, 10:22
- |
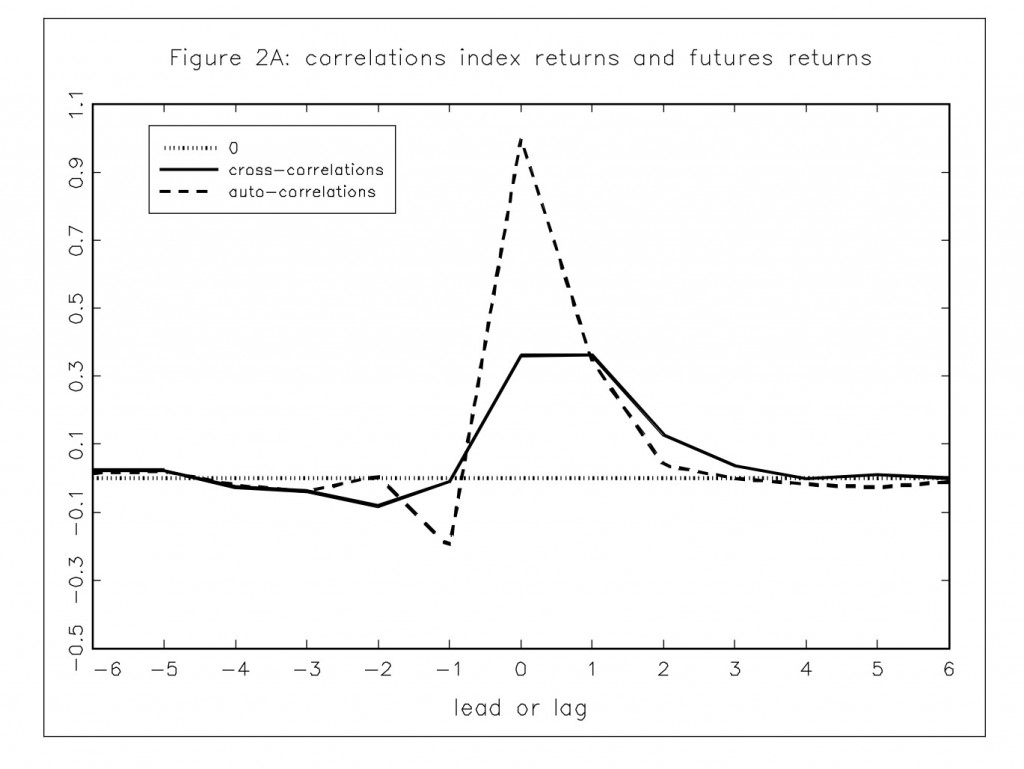
Трейдеры, которые приобрели мою программу robot_uralpro (см. пост на смарт-лабе), спрашивают, можно ли доработать алгоритм для применения его на современном рынке? Напомню, стратегия робота основана на взаимоотношении цен синтетического индекса, составляемого динамически из рыночных цен акций, входящих в индекс РТС, и фьючерса RI. Идея «одноногого» статистического арбитража, реализованного в роботе, будет работать и сейчас, только в том случае, если научиться правильно определять, какой актив опережает другой в смысле динамики их цен. Эта статья посвящена правильному выявлению такого взаимодействия, которое в англоязычных источниках называется «lead-lag relationship» -опережение-отставание между разными активами.
Те алготрейдеры, кто не приобретал robot_uralpro, тоже сочтут эту статью полезной, так как lead-lag relationship может использоваться в стратегиях парного трейдинга и им подобным. Например, определив такое взаимодействие, можно исключить из парного трейдинга один из активов ( с учетом того, конечно, что отношение торгуемых инструментов было описано четкой моделью) и значительно увеличить тем самым прибыльность стратегии.
( Читать дальше )
Стратегия "Гэп на открытии"
- 14 апреля 2015, 10:07
- |
Небольшое исследование стратегии «Гэп на открытии рынка» в блоге Pawel Lachowicz. Автор случайным образом выбрал 10 акций из состава индекса Доу-Джонса, и провел бэктестирование вышеуказанной стратегии. Основные параметры алгоритма:
вход в позицию: если цена открытия актива в день t выше цены закрытия актива в день t-1, и если минимальная цена актива в день t выше максимальной цены актива в день t-1, акция покупается на следующий день, причем цена покупки устанавливается равной цене закрытия дня t;
выход из позиции происходит просто по временному критерию — акция удерживается после входа от 1 до 21 дня, количество дней — это параметр оптимизации для бэктеста.
Сначала бэктест прогоняется на каждом активе отдельно на выборке длительностью 1 год. Пример для акции AXP — сколько в течение этого времени обнаружено условий для входа в позицию (обозначены кружками):
( Читать дальше )
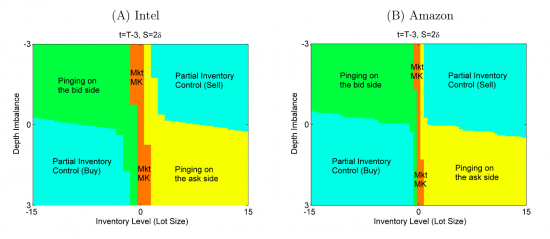
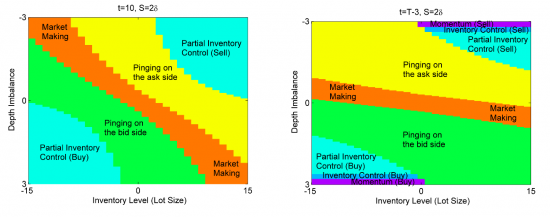
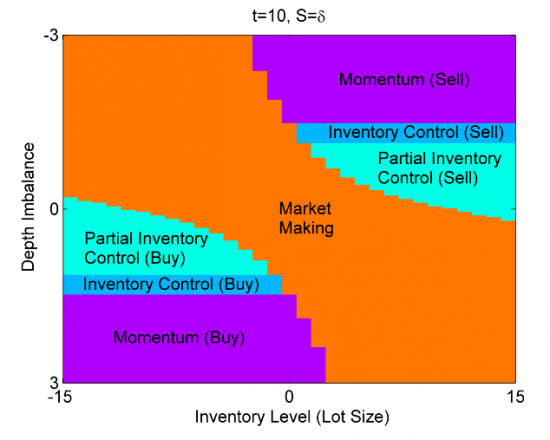
Алгоритмы маркетмейкера. Часть 5
- 09 апреля 2015, 11:27
- |
Продолжаем разбирать численное решение уравнения Хамильтона-Якоби-Беллмана. В прошлой части мы составили выражение для оператора 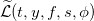 , в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью
, в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью 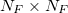 , где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в
, где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях, в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в
( Читать дальше )
Алгоритмы маркетмейкера. Часть 4
- 07 апреля 2015, 11:25
- |
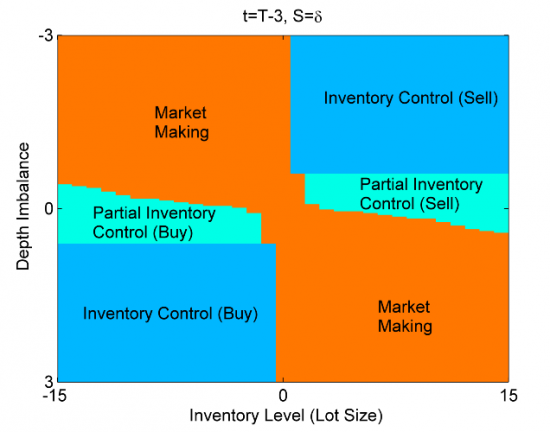
Прошлые части цикла здесь. В этой части статьи мы найдем численное решение системы уравнений оптимального управления позицией маркетмейкера. Такое решение легко запрограммировать и использовать в реальной торговле для контроля за лимитными и маркет ордерами в соответствии с полученными стратегиями θmk,θtk. Для упрощения разложим функцию владения на слагаемые, чтобы получить сокращенную функцию владения v(t,y,f,s), которая представляет собой только динамическую составляющую основной функции:
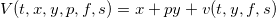
( Читать дальше )
Алгоритмы маркетмейкера. Часть 3
- 02 апреля 2015, 09:46
- |
Продолжаем разбирать работу JIANGMIN XU «Optimal Strategies of High Frequency Traders». Чтобы составить уравнение оптимального контроля, сначала сформулируем проблему оптимизации алгоритма при используемых стратегиях θ, как достижение максимума следующего матожидания:
![Алгоритмы маркетмейкера. Часть 3 \max_{\theta^{mk},\theta^{tk}}\mathbb{E}_0[X_T-\gamma\int^T_0 Y^2_{t-}d[P,P]_t]](http://mathurl.com/pthr6jr.png) ,
,
( Читать дальше )
Алгоритмы маркетмейкера. Часть 2
- 31 марта 2015, 11:10
- |
В прошлой части мы рассмотрели оптимальное управление inventory risk в маркетмейкерском алгоритме. Напомню, что формулы для нейтральной цены и оптимального спреда между лимитными ордерами были получены при допущении, что цена следует геометрическому броуновскому движению. Управление inventory risk для моделей цены, более приближенными к реальности, рассматривается, например, в статье Pietro Fodra & Mauricio Labadie «High-frequency market-making with inventory constraints and directional bets» . Однако, применить напрямую на практике алгоритмы из этих статей вряд ли получится, так как в них не учитывается действие adverse selection risk. Поэтому в данной части рассмотрим работу JIANGMIN XU «Optimal Strategies of High Frequency Traders», в которой автор делает попытку учесть этот вид риска, конечно, наряду с inventory risk.
( Читать дальше )
Алгоритмы маркетмейкера. Часть 1
- 26 марта 2015, 11:26
- |
В биржевой торговле существует ряд алгоритмов, которые можно отнести к маркетмейкерским. Как правило, это означает выставление лимитных ордеров по обе стороны стакана, то есть как на покупку, так и на продажу, и целью такого алгоритма является получение прибыли от спреда - разницы между этими лимитными ордерами. Простейшая стратегия подобного рода — постановка ордеров одновременно на лучший бид и лучший аск — будет убыточной из-за действия следующих факторов:
1. Вероятность взятия ордера на стороне, противоположной движению цены в большинстве случаев выше, чем на стороне по направлению движения. То есть, если цена актива растет, то чаще будут исполняться ордера, выставленные на продажу, а ордера на покупку, соответственно — реже, в результате возникает убыточная позиция. В англоязычной литературе этот эффект называется
( Читать дальше )
Исходники robot_uralpro ЛЧИ 2010
- 25 марта 2015, 11:49
- |
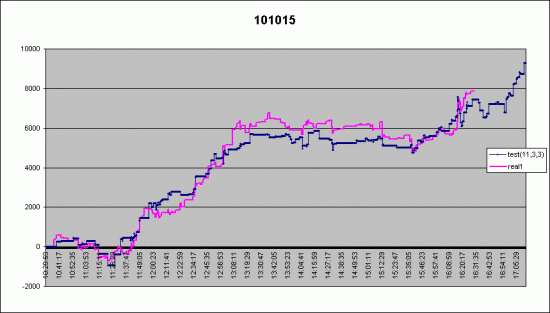
В своем прошлом посте я обещал раскрыть алгоритм robot_uralpro (25 место ЛЧИ 2010, HFT), но получил в личку много просьб от читателей смарт-лаба ( видимо тех, кто занимается алгоритмической торговлей) этого не делать. Аргументация, в общем, сводилась к тому, что народ у нас достаточно образованный и этим разоблачением алгоритма я могу наплодить армию конкурентов для роботорговцев. И это правда - например, когда в 2009 году начинал разработку стратегий, я вообще не знал ничего о том, как работают HFT, но, шаг за шагом, в условиях почти нулевой информации, удалось создать прибыльный алгоритм. Тем не менее, свои обещания надо выполнять, поэтому я принял решение, которое позволит трейдерам, серьезно интересующимся высокочастотной торговлей, получить обещанное, и даже больше, но в то же время значительно ограничит распространение: я предоставлю не только описание алгоритма, но и сам исходный код робота на C# с подробными комментариями точно в том виде, в котором он работал на ЛЧИ 2010, но все это — не бесплатно . Далее причины, почему покупать это не нужно:
( Читать дальше )
теги блога uralpro
- ARIMA
- data feed
- ETF
- FORTS
- GARCH
- HFT
- IQFeed
- mean reversion
- momentum
- python
- S&P500
- VIX
- VPIN
- алгоритм
- алгоритм торговли
- алгоритмическая торговля
- алгоритмы
- алгоритмы торговли
- алготрейдинг
- альфа-сигналы
- андрей мовчан
- Биржевые роботы
- биткоины
- Блэк-Шоулз
- бэктестинг
- возврат к среднему
- волатильность
- высокастотники
- высокая доходность
- высокочастотная торговля
- высокочастотный трейдинг
- генетические алгоритм
- генетические алгоритмы
- гэп
- доходность трейдеров
- импульс
- импульсная система
- индексы
- интервью
- итоги
- итоги 2016
- Итоги 2018
- книга заявок
- коинтеграция
- колокейшн
- Конференции смартлаба
- конференция
- корреляция
- криптовалюта
- лчи
- маркет дата
- маркет мейкер
- марковиц
- марковский процесс
- математические модели
- машинное обучение
- модели
- Модели рынка
- модель
- модель Маркова
- Оптимизация портфеля
- опционные модели
- опционы
- Парный трейдинг
- парный трейдинг
- подготовка данных
- поток ордеров
- Публикации
- публикация
- разработка алгоритма
- разработка торговых систем
- раундтрип
- регрессия
- результат торговли
- робот
- роботы
- роботы в биржевой торговле
- скользящая средняя
- стакан
- стоп лосс
- стратегия
- торговля волатильностью
- торговые алгоритмы
- торговые стратегии
- улыбка волатильности
- ФОРТС
- Херст
- эквити
- язык R