Блог им. uralpro
Линейная регрессия с использованием фильтра Калмана
- 23 апреля 2015, 10:12
- |
Линейная регрессия часто используется для вычисления пропорции хеджирования в парном трейдинге. В идеальной ситуации коэффициенты этой регрессии — наклон линии регрессии и свободный член (пересечение) остаются всегда постоянными. Однако в реальности все, конечно, не так радужно, и значения этих параметров постоянно меняются во времени. Как правильно вычислять коэффициенты регрессии, чтобы избежать подгонки к текущей ситуации, рассматривается в статье "Online Linear Regression using a Kalman Filter". Для этой цели в данной публикации используется фильтр Калмана.
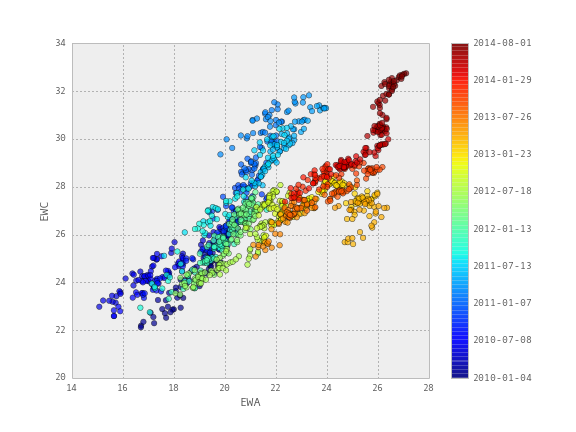
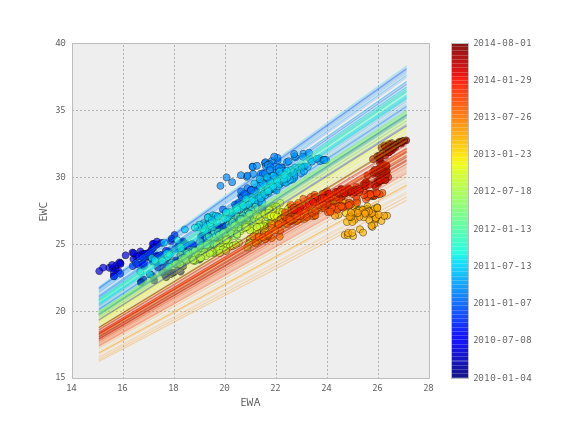
Для тестирования берутся исторические цены закрытия двух биржевых фондов ETF — австралийского EWA и канадского EWC с 2010 по 2014 год. Динамика цен этих фондов показывает взаимосвязь, что продемонстрировано на диаграмме рассеивания в заглавии поста. Однако по этому же графику видно, что эту взаимосвязь невозможно описать с помощью линейной регрессии с постоянными коэффициентами.
Приведем сначала уравнение линейной регрессии:
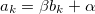
где ak, bk- приведенные цены фондов EWC и EWA соответственно, а β, α- коэффициенты регрессии — угол наклона и пересечение соответственно. Перепишем уравнение в матричной форме:
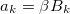
![Линейная регрессия с использованием фильтра Калмана \beta=[\beta\;\alpha]](http://mathurl.com/p9qduof.png)
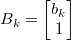
Фильтр Калмана — это модель пространства состояний, которая применяется рекурсивно на входном потоке зашумленных данных для получения статистически оптимальной оценки состояния системы. Общая форма фильтра Калмана содержит передаточное уравнение и уравнение наблюдений:
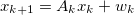
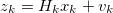
где xk, zk- вектор скрытых состояний и вектор наблюдений в момент времени k, Ak, Hk- матрица переходов и наблюдений соответственно, wk,vk- векторы гауссовского шума с нулевым средним.
Для наших целей предположим, что вектор состояний xk соостветствует вектору коэффициентов регрессии β. Также предположим, что угол наклона и пересечение следуют процессу случайного блуждания (random walk), тогда Ak будет равна матрице идентичности I (матрице, где на главной диагонали единицы, остальные элементы — нули). В этом случае передаточное уравнение запишется:
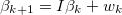
то есть β в следующий момент времени равна β в текущий момент времени плюс шумовая составляющая.
На следующем шаге применим нашу модель к уравнению наблюдений фильтра Калмана. Для этого приведенные цены закрытия актива EWC обозначим как вектор наблюдений zk, и матрицу наблюдений Hk представим как вектор размерности 1х2, содержащий в первой колонке приведенные цены закрытия EWA и единицами во второй колонке, подобно нашему вектору Bk. Таким образом, это просто линейная регрессия между двумя активами. Для подпрограммы на Python - pykalman, конструирующей фильтр Калмана, матрица наблюдений obs_mat выглядит так:
obs_mat = np.vstack([data.EWA, np.ones(data.EWA.shape)]).T[:, np.newaxis]
array([[[ 19.36, 1. ]],
[[ 19.42, 1. ]],
[[ 19.49, 1. ]],
...,
[[ 26.02, 1. ]],
[[ 26.24, 1. ]],
[[ 26.42, 1. ]]])
Последнее, что нужно сделать — определить шумовые составляющие wk,vk. Установим ковариацию наблюдений vk, как единичный вектор. Тогда будем трактовать ковариацию переходов, wk, как настраиваемый параметр для управления скоростью изменения коэффициентов регрессии:
delta = 1e-5 trans_cov = delta / (1 - delta) * np.eye(2)
Далее установим класс фильтра Калмана KalmanFilter из модуля pykalman :
kf = KalmanFilter(n_dim_obs=1, n_dim_state=2,
initial_state_mean=np.zeros(2),
initial_state_covariance=np.ones((2, 2)),
transition_matrices=np.eye(2),
observation_matrices=obs_mat,
observation_covariance=1.0,
transition_covariance=trans_cov)
и вычислим средние значения и ковариацию состояний:
state_means, state_covs = kf.filter(data.EWC.values)
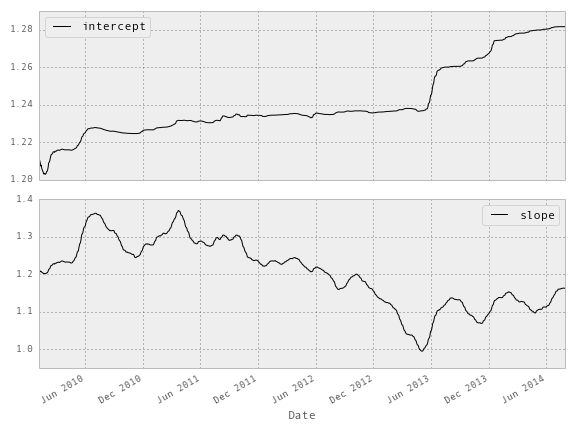
В итоге мы получаем графики изменений коэффициентов регресии — угла наклона (slope) и пересечения (intercept):
Более наглядно можно показать, как подстраиваются коэффициенты регрессии в течение времени на диаграмме рассеивания активов EWA и EWC:
Думаю, те, кто практиковал парный трейдинг, найдет эту статью очень полезной, так как она решает один из главных вопросов в этом виде торговли — каким образом строить линейную регрессию, не попадая под обычную подгонку текущего состояния ценового спреда.
Другие стратегии, применяемые в алгоритмической торговле и биржевых роботах смотрите в моем блоге и на сайте.
теги блога uralpro
- ARIMA
- data feed
- ETF
- FORTS
- GARCH
- HFT
- IQFeed
- mean reversion
- momentum
- python
- S&P500
- VIX
- VPIN
- алгоритм
- алгоритм торговли
- алгоритмическая торговля
- алгоритмы
- алгоритмы торговли
- алготрейдинг
- альфа-сигналы
- андрей мовчан
- Биржевые роботы
- биткоины
- Блэк-Шоулз
- бэктестинг
- возврат к среднему
- волатильность
- высокастотники
- высокая доходность
- высокочастотная торговля
- высокочастотный трейдинг
- генетические алгоритм
- генетические алгоритмы
- гэп
- доходность трейдеров
- импульс
- импульсная система
- индексы
- интервью
- итоги
- итоги 2016
- Итоги 2018
- книга заявок
- коинтеграция
- колокейшн
- Конференции смартлаба
- конференция
- корреляция
- криптовалюта
- лчи
- маркет дата
- маркет мейкер
- марковиц
- марковский процесс
- математические модели
- машинное обучение
- модели
- Модели рынка
- модель
- модель Маркова
- Оптимизация портфеля
- опционные модели
- опционы
- Парный трейдинг
- парный трейдинг
- подготовка данных
- поток ордеров
- Публикации
- публикация
- разработка алгоритма
- разработка торговых систем
- раундтрип
- регрессия
- результат торговли
- робот
- роботы
- роботы в биржевой торговле
- скользящая средняя
- стакан
- стоп лосс
- стратегия
- торговля волатильностью
- торговые алгоритмы
- торговые стратегии
- улыбка волатильности
- ФОРТС
- Херст
- эквити
- язык R



















вся суть парного в том, что имеем 10 активов… всего будет 50 пар… из этих 50 пар можно выбрать 2-3 стабильные торгуемые обычными скользящими средними без всякого мозготраха
1 скользящая средняя = ФНЧ… на любом фильтре, в том числе и калмана есть отставание… чем выше порядок фильтра тем больше отставние-задержка
2 дык ты не вычитай один актив из другого, а дели один на другой… типа брент/голд
Что мы выигрываем по описанному автором методу по сравнению с подходом " в лоб"? Ну, кроме скорости вычислений, которая, имхо, не особо напрягает всех, кроме высокочастотников.
Удачи!