Индикаторы осцилляторы это статистические аттракторы.

Аттра́ктор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Аттрактором может являться притягивающая неподвижная точка (к примеру, в задаче о маятнике с трением о воздух), периодическая траектория (пример — самовозбуждающиеся колебания в контуре с положительной обратной связью), или некоторая ограниченная область с неустойчивыми траекториями внутри (как у странного аттрактора).






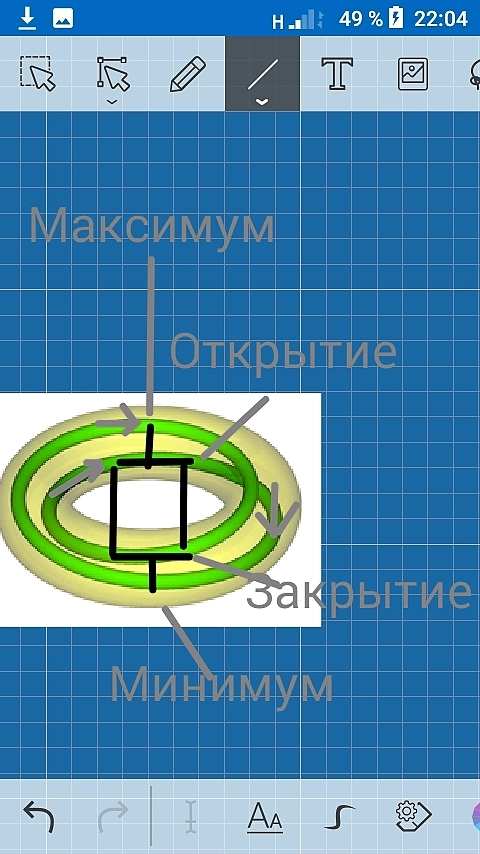
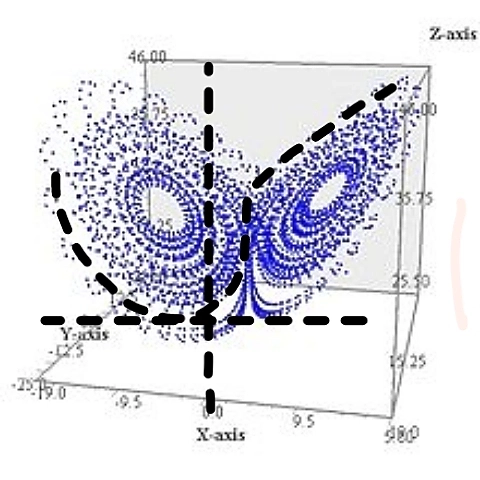
Классический пример странного аттрактора — аттрактор Лоренца

МACD



Соленоид Смейла — Вильямса — пример обратимой динамической системы

RSI



Фазовый портрет примера Боуэна

DeMarker


В теории динамических систем, перемешивание — свойство системы «забывать» информацию о начальном условии с течением времени.

Фактор риска!
Используя осцилляторы нужно отличать до и после перемешивания.
Недавно наблюдая за MACD после перемешивания, цена снизилась и начала боковое движение, индикатор забыл об снижении и начал стремиться к нулю, вместо того чтобы показывать боковик. На истории этого может невидно, тем более тем кто торгует по 4H такое событие может испортить не один день торговли.