Стоп-лосс и тейк-профит. Где ставить. Часть 1. Самый длинный путь к сливу

Начало здесь

smart-lab.ru/blog/755391.php

Я сразу в математику. Приведу обозначения, потом их поясню.

Обозначения:

D — депозит, (доллары США),
c  — цена пункта, (доллары США / пункт),
s  — спред (пункты), его будем считать фиксированным.
p  — уменьшение депозита после срабатывания стопа. 0 < p < 1,
Ж — (от слова «жопа») уровень слива 0 < Ж < 1,
k  — количество сделок для слива.

Поясню. после срабатывания стопа депозит уменьшается. Был D, а стал D*p. 
Нам для дальнейшего придется формально задать величину депозита, при достижении которой мы будем считать депозит слитым. Был депозит D, а стал D*Ж. В конечных формулах этот параметр исчезнет, а потому позволил себе букву, которая для формул не характерна.

Поехали!

Представим себе, что при каждом входе в рынок, мы выбираем объем сделки таким, чтобы имеющийся в наличии депозит, деленный на цену пункта был бы одинаковым для всей серии сделок. Есть, допустим, у вас 100 долларов, вы делаете ставку со стоимостью пункта 1 доллар/пункт. отношение этих величин равно 100. Потом у вас осталось, например, 60 долларов и вы выбираете объем 0,6 доллара/пункт. Отношение этих величин равно 100. И так для всех сделок. Таким образом, вы при каждом входе в рынок играете с ним в одну и ту же игру. Вошли, за спиной 100 пунктов, причем всегда.

При каждом входе в рынок вы устанавливаете стоп-лосс так, чтобы после его срабатывания депозит уменьшался бы в p раз. При описанном выше алгоритме выбора объема сделки, стоп-лосс каждый раз будет на одном и том же расстоянии (в пункта), и мы снова убеждаемся в том, что при каждом входе мы играем с рынком в одну и ту же игру независимо от оставшихся средств.

В принципе, мы можем слить депозит за одну сделку. Приведу численный пример.

Пусть депозит равен 100 долларов. Задаем уровень Ж = 0,1 (то бишь если от депозита осталось 10%, то мы считаем его слитым под корень).
Делаем ставку объемом 1 доллар за пункт, устанавливаем стоп-лосс на расстоянии 90 пунктов от входа, и ждем. Сколько же пунктов надо пройти рынку чтобы коснуться стопа? Поскольку у нас есть спред, допустим 3 пункта, то рынку до стопа идти 90 — 3 = 87 пунктов.

Можем слить депозит и за две сделки, надо только правильно выбрать стоп-лосс, чтобы наша стандартная игра с рынком не теряла своего характера.
В нашем численном примере начальный депозит равен 100 долларам. Это значит, что для выбора стопа мы должны положить, что 

Ж*100 долларов= 100 долларов * p^2 

(вот этой шляпкой "^" обозначена операция возведения в степень. В данном случае, это возведение в квадрат). 
Из этого соотношения следует, что 

p = Ж^(1/2) = 0.1^(1/2) = 0.3162

В первой сделке мы выбираем объем таким, чтобы D/c = 100, то есть с = 1 доллар за пункт. Депозит в первой сделке уменьшается до

100 * 0,3162 = 31,62 то есть на 68,38 доллара

то есть стоп должен стоять на расстоянии 68,4 пункта. Рынку, с учетом спреда, для его срабатывания надо пройти 68,4 — 3 = 65,4 пункта.

Во второй сделке мы выбираем объем таким, чтобы цена пункта составляла 0,3162 доллара за пункт, тогда мы опять имеем
31,62/0,3162 = 100 пунктов. для достижения уровня Ж = 10 долларов, надо пройти (31,62 — 10)/0,3162 = 68,4 пункта, то есть то же расстояние что и первой сделке. Рынку во второй сделке надо пройти те же 68,4 — 3 = 65,4 пункта.

Два примера я привел (все численные результаты приближенные, а потому не придирайтесь). Что здесь важно?

В первом случае до слива рынок прошел 87 пунктов, а во втором случае ему для этого потребовалось два прохода по 65,4 пункта, то есть 130,8 пункта! То бишь при втором подходе полный слив Ж становится дальше на 130,8 — 87 = 43,8 пункта!!!

А что будет, если поход к Ж разделить на три части? На четыре? «Вот тут я и начал объяснять» ©

Чтобы пройти до уровня Ж за k сделок, мы должны выбрать величину p равной

p = Ж^(1/k)

При это м рынку за все k сделок надо пройти (в пунктах)

f(k) = [D/c*(1-p)-s]*k = [D/c*(1- Ж^(1/k)]*k

Давайте нарисуем график этой функции. Вот он для случая D/c = 100, s = 3.

Верхний график — расстояние до слива в пунктах, нижний — расстояние до стопа.





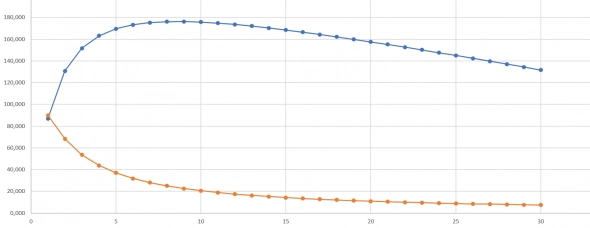
Прикол в том, что эта кривая имеет максимум, то есть при некотором k слив находится максимально далеко. В приведенном примере рынку надо пройти в общей сложности 176 пунктов, при этом стоп всегда ставится на расстоянии 22,6 пункта.

Конечно, хочется продифференцировать функцию f(k) по аргументу k, приравнять ее к нулю, и получить формулу для максимума и для стопа.
Я это сделал, получил вот что

f`(k) = D/c — s — (D/c)* Ж^(1/k) + (D/c)* Ж^(1/k)*(1/k) *ln(Ж^(1/k) = 0

Если учесть, что Ж^(1/k) = p, то получим

1 — (s*c/D) — p + p*ln(p) = 0

А вот хрен-то это уравнение получится решить в явном виде относительно p. У меня не получилось.
Короче, для оценок приходится обходиться графикой. это просто, тем более, что если и нужно что, то с невысокой точностью.

Все на сегодня. Следующий пост о наилучшем тейк-профите. Оказывается, что существует самый короткий путь к успеху!
Ура! На сегодня все.