Критическая масса и критическое значение аналогичных стратегий

В первой части мы анализировали критический порог статистической значимости для сложных композитных систем на примере модели AR. В этот раз мы попытаемся быть чуть ближе к делу и проведем тесты для набора трендовых систем на базе Simple Moving Average. В качестве примера возьмем самый ликвидный фьючерс — белый шум, для которого заранее известно, что он абсолютно «не торгуемый» и попытаемся всё же что-нибудь под него подобрать из соображений трендовости «больших денег» и саморефлексии участников торгов. 

Сгенерируем набор из 10 стратегий с периодом 10*i, i=1,2,...10. 

Nstr=10; 
x=randn(10000,1); 
y=[x(2:end);0]; 
M=zeros(10000,Nstr);
for i=1:Nstr; 
    M(:,i)=tsmovavg(x,'s',10*i,1); 
end; 
M(1:Nstr*10,:)=0; R=M.*y;   

И оценим порог 70% статистической значимости коэффициента шарпа стратегии без учета размерности набора стратегий: 



И с учетом размерности :



Эффективная размерность для набора из 10 SMA с различным периодом получилась 3.7368, что хорошо видно из корреляционной матрицы -



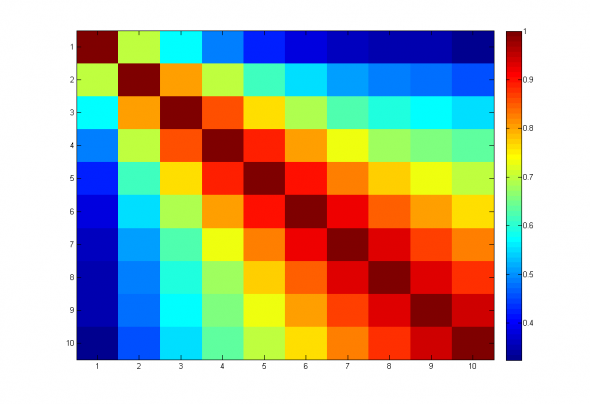
Рис 1. Корреляционная матрица набора трендовых стратегий с различным периодом.




Заметим, что для лучшего соответствия эмпирическим данным, мы заменили оценку эффективной размерности :



где Csqrt — матрица корней из корреляционных коэффициентов стратегий, так что обобщенное критическое значение получилось равным :
       




Изобразим полученные результаты тестов и полученные доверительные интервалы :


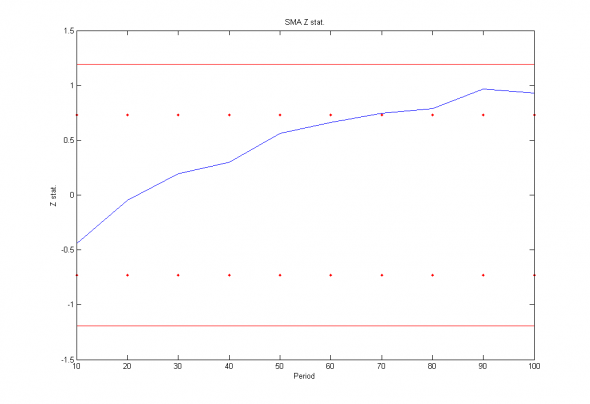
Рис 2. Z статистика для стратегий основанных на скользящих средних случайного блуждания в зависимости от периода (синяя линия), «классический» Z тест (красные точки) и модифицированный Z тест (красная линия). 


Хорошо виден эффект слабой контрендовости в ближней зоне, связанный с влиянием «срочности» расчетов и «игрой по стопам» против трендового эффекта в дальней зоне, связанного с медленным переливанием «больших» капиталов. Тем не менее, даже не смотря на полное соответствие случайной реализации случайного блуждания с нашими глубоко профессиональными представлениями о рынке и на то, что сама совокупность стратегий образует достаточно широкое «облако антиподгона»,  с точки зрения статистики мы не можем утверждать, что способны обыграть случайное блуждание с вероятностью хотя бы 70%.


Что же, рассмотрим наши стратегии поближе -

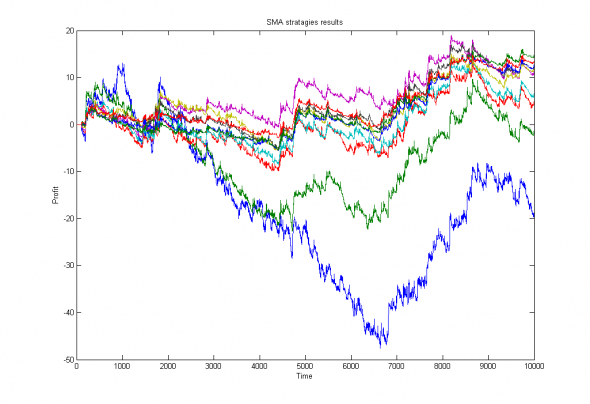
Рис 3. Изображение прибыли, полученной по различным стратегиям.

 
На первый взгляд ничего интересного, но из-за достаточно широкого «облака»,  характерного для данного класса стратегий (SMA), мы получаем возможность перескакивать с одного прибыльного тренда на другой и получать дополнительное преимущество от адаптации к изменяющимся неэффективностям рынка.


Проведем адаптативный run forward rolling active adaptation OOS тест  (IS=600, oOS=300) на сетке  параметров ( T=10*i,i=1,2,..10 ) :

K=600; Q=300; 
IS=zeros(K,1); 
Roos=zeros(10000,1); 
for i=K:Q:10000-Q; 
     IS=x(i-K+1:i); 
     M=zeros(K,10); 
     y=[IS(2:end);0]; 
     for j=1:10; 
          M(:,j)=tsmovavg(IS,'s',10*j,1).*y; 
     end; 
     M(1:100,:)=0;
     sharp=mean(M)./std(M); 
     [a,per]=max(sharp); 
     if a>0; 
        Roos(i+1:i+100)=R(i+1:i+100,per); 
     end; 
end; 
plot(cumsum(Roos));  title('OOS test for SMA strategies at random noise'); xlabel('Time'); ylabel('Profit');

И графически изобразим полученные результаты:


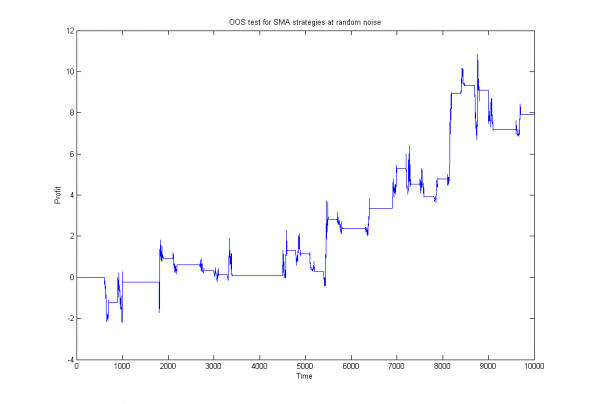
Рис 4. OOS тест для набора трендовых стратегий с переоптимизацией каждые 300 отсчетов на интервале 600 отсчетов.



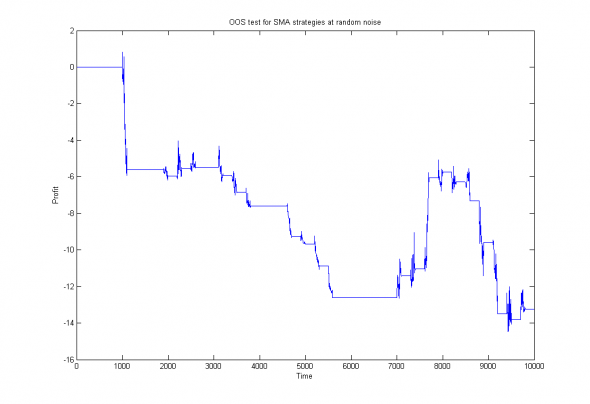
Рис 5. OOS тест для набора трендовых стратегий с переоптимизацией каждые 300 отсчетов на интервале 1000 отсчетов.


Что лишний раз подтверждает простую истину — закономерности случайного блуждания постоянно изменяются и прошлые закономерности быстро устаревают, поэтому оптимизировать портфель стратегий  нужно как можно чаще и на как можно более поздних, ещё репрезентативных данных. 





И какой из этого всего можно сделать вывод? А очень простой :

Что за новость, вот те на!
Пришла новая беда –
Дата-сайнс и Машин-лернинг
Применяют на ура!

Только лучше не спеши,
Сядь, подумай и реши.
Оверфитнуться здесь просто,
На бэктесты не греши.

Запросто она, цена,
Выйдет боком не туда
И утащит OOS тесты
За собою вникуда.

Замест чем опять гадать –
Где купить, а где продать?!
Взял бы лучше опционов,
Чтобы всё не проиграть!

Опционы это да –
Не случайная игра.
С ними можно спать спокойно!
…От утра и до утра.

Вон, смотри, как Старый Бес,
На какую гору влез!?
И в обчественном сознаньи
У него почет и вес!

Эту ж грамоту отложь,
Лишних сложностей не трожь.
Ежли не взлетишь как птица…,
То хотя бы доползешь.