13 марта 2021, 16:53
Физико-математические основы Грааля. Часть 9. Нестационарность рынка.
Вспоминаю диалог с Колдуном:
— Запомни, рынок стационарен в узком смысле, однако, страждущие не могут это узреть. Ищи стационарность и обрящешь.
— Слушаюсь, Мастер...
— Ступай, Тень, и не тревожь меня более.
Как же так? Какая еще стационарность? Ведь всем известно, что никакой стационарности нетути, что рынок нестационарен по определению и этот факт является первопричиной отсутствия стабильно зарабатывающей торговой системы практически у всех трейдеров...
Если исходить из парадигмы немарковского случайного процесса, описываемого уравнением:
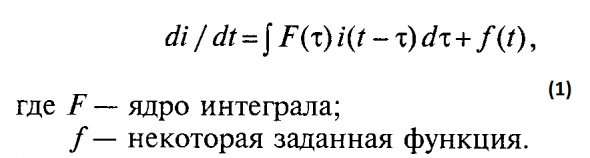
то, очевидно, что на рынке f(t) — это плотность вероятности тиковых приращений, которая является предопределенной для каждой валютной пары и принадлежит к классу гамма-распределений.
Примем за основную гипотезу, что генеральная совокупность приращений образует именно заданную плотность вероятности некоего ГПСЧ (в теме https://smart-lab.ru/blog/616897.php было показано, что данный ГПСЧ представляет из себя произведение СЧ гауссовского распределения и распределения Эрланга, т.е. расстояния, которые проходит броуновская частица за экспоненциальные промежутки времени).
В этом случае, мы вправе использовать известную формулу Эйнштейна-Смолуховского:

Для семейства гамма-распределений, коэффициент диффузии D определяется выражением:
D = S*(b^2)
где
S — некий параметр формы данного распределения, а b - это среднее значение модулей приращений

при N --> к бесконечности.
Фактически, мы постулируем, что параметр b = const и является уникальным для каждой валютной пары.
Т.о. рынок действительно является стационарным в том смысле, что распределение тиковых приращений для каждой валютной пары является неизменным и задается раз и навсегда. А то, что мы видим на примере выборок из генеральной совокупности приращений — это ерунда и использовать в расчетах выборочные дисперсию и матожидание распределения приращений нельзя ни в коем случае.
Поэтому, в формуле

нестационарным остается только интенсивность tau (количество пришедших тиков за определенный промежуток времени) тикового потока котировок.
Что же с этим делать?
А, пожалуй, — ничего. Надо принять это «как есть» ибо так посоветовал Волшебник.
Посмотрим график для пары AUDCHF за случайный промежуток времени
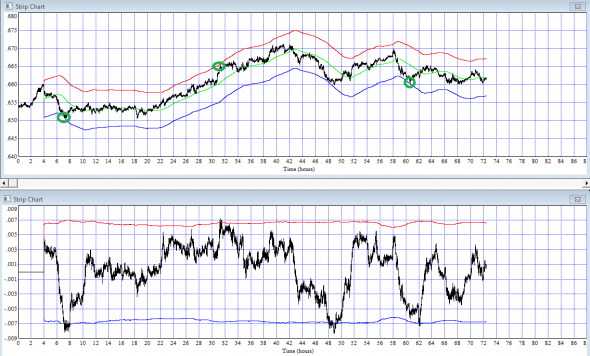
Точки входа отмечены зелеными кружками.
Выход — при возврате к средней.
На нижнем графике видно, что дисперсионный канал незначительно меняется при изменении интенсивности тикового потока котировок, но, в целом это не оказывает существенного влияния на стратегию.
До встречи.
Toddler.
PS
Только — тсссс… Никому — ни слова, ни полслова об услышанном. Колдун и Девять Стражей Грааля осерчать могут. Помилосердствуйте....
— Запомни, рынок стационарен в узком смысле, однако, страждущие не могут это узреть. Ищи стационарность и обрящешь.
— Слушаюсь, Мастер...
— Ступай, Тень, и не тревожь меня более.
Как же так? Какая еще стационарность? Ведь всем известно, что никакой стационарности нетути, что рынок нестационарен по определению и этот факт является первопричиной отсутствия стабильно зарабатывающей торговой системы практически у всех трейдеров...
Если исходить из парадигмы немарковского случайного процесса, описываемого уравнением:
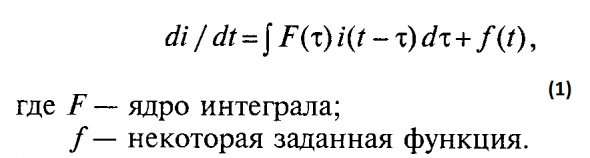
то, очевидно, что на рынке f(t) — это плотность вероятности тиковых приращений, которая является предопределенной для каждой валютной пары и принадлежит к классу гамма-распределений.
Примем за основную гипотезу, что генеральная совокупность приращений образует именно заданную плотность вероятности некоего ГПСЧ (в теме https://smart-lab.ru/blog/616897.php было показано, что данный ГПСЧ представляет из себя произведение СЧ гауссовского распределения и распределения Эрланга, т.е. расстояния, которые проходит броуновская частица за экспоненциальные промежутки времени).
В этом случае, мы вправе использовать известную формулу Эйнштейна-Смолуховского:
Коэффициент диффузии броуновской частицы связывает средний квадрат её смещения x (в проекции на произвольную фиксированную ось) и время наблюдения τ:

Для семейства гамма-распределений, коэффициент диффузии D определяется выражением:
D = S*(b^2)
где
S — некий параметр формы данного распределения, а b - это среднее значение модулей приращений

при N --> к бесконечности.
Фактически, мы постулируем, что параметр b = const и является уникальным для каждой валютной пары.
Т.о. рынок действительно является стационарным в том смысле, что распределение тиковых приращений для каждой валютной пары является неизменным и задается раз и навсегда. А то, что мы видим на примере выборок из генеральной совокупности приращений — это ерунда и использовать в расчетах выборочные дисперсию и матожидание распределения приращений нельзя ни в коем случае.
Поэтому, в формуле

нестационарным остается только интенсивность tau (количество пришедших тиков за определенный промежуток времени) тикового потока котировок.
Что же с этим делать?
А, пожалуй, — ничего. Надо принять это «как есть» ибо так посоветовал Волшебник.
Посмотрим график для пары AUDCHF за случайный промежуток времени

Точки входа отмечены зелеными кружками.
Выход — при возврате к средней.
На нижнем графике видно, что дисперсионный канал незначительно меняется при изменении интенсивности тикового потока котировок, но, в целом это не оказывает существенного влияния на стратегию.
До встречи.
Toddler.
PS
Только — тсссс… Никому — ни слова, ни полслова об услышанном. Колдун и Девять Стражей Грааля осерчать могут. Помилосердствуйте....
Читайте на SMART-LAB:
⚡️ Развиваем синергию внутри Группы Займер
Важнейшим эффектом сделок по покупке «Таксиагрегатор» и IntellectMoney будет развитие синергических связей между компаниями Группы. 🟢 Займер будет предоставлять займы водителям, подключенным к...
13.02.2026

Как прошла экскурсия на лазерное производство
На прошлой неделе мы организовали поездку для представителей медиа и финансового сообщества на завод лазерной дочки SOFL — VPG LaserONE (входит в наш кластер «СФ Тех»). В экскурсии приняли участие...
12.02.2026











Сходимость суммы к b при N, стремящемся к бесконечности, говорит не о стационарности, а о некой форме ограниченности котировок (что естественно).
Стационарность у рядов приращений цен отсутствует (что несложно проверяется), а вот эргодичность в некоей форме присутствует. Что и позволяет проводить общие рассуждения.
С уважением