Моделирование Торговых Систем на Python. 2.

Тем, кто не читал предыдущий топик этой темы, рекомендую для начала ознакомиться с ним [1].

В комментариях к предыдущему топику меня критиковали за неоптимальность кода Python. Однако, текст читают люди с совершенно разной подготовкой — от почти не знающих Python или знающих другие языки программирования, до продвинутых пользователей. Последние легко могут обнаружить неоптимальность кода и заменить его своим. Тем не менее, код должен быть доступен и новичкам, возможно не обладающим знанием пакетов и продвинутых методов. Поэтому, в коде я буду, по возможности, использовать только базовые конструкции Python, не требующие глубоких знаний, и которые могут легко читаться людьми, программирующими на других языках. Вместе с тем, по мере изложения, без фанатизма, буду вводить и новые элементы Python.
Если вы хотите как-то улучшить или оптимизировать код, приводите его в комментариях — это только расширит и улучшит изложенный материал.

Ну, а сейчас мы займемся разработкой и тестированием индикаторов. Для начала нам нужна простейшая стратегия с использованием МА — его и построим. Самой лучшей по характеристикам МА является ЕМА. Формула ЕМА:

    Y(i) = a0*X(i) + b1*Y(i-1), где a0 + b1 = 1.

Однако коэффициенты ЕМА мы будем считать по другому:

    a0 = 1/(1+T/(2*pi) и b1 = T/(2*pi)/(1+T/(2*pi)), где pi = 3.14...,

что превращает ЕМА в полноценный Фильтр Нижних Частот (ФНЧ) 1-го порядка, в котором Т соответстует частоте отсечки фильтра fо = 1/T. В отличие от ЕМА, здесь параметр Т приобретает явный физический смысл, сам фильтр имеет прогнозируемые свойства, и с таким фильтром легко работать. Ну, коли он теперь фильтр, и назовем индикатор по другому cF1Bat().

Для проектирования фильтра в Python мы будем использовать классы (class). Для тех, кто не знаком с Объектно Ориентированным Программированием (ООП), class — это изолированный кусок кода, содержащий (инкапсулирующий) в себе данные и функции (методы). Объявляя или инициализируя class, мы создаем объект. Собственно, объявляя массив, структуру, строку символов или даже переменную, мы тоже создаем объекты под которые выделяется память. Все примерно тоже самое, ничего необычного.)
Ну, и сам код индикаторов:

# -*- coding: utf-8 -*-
"""
Created on Mon May 12 10:07:14 2020

@author: 3Qu
"""

import math


# Фильтр LPF 1-го порядка
class cF1Bat():

    def __init__(self, per, x):
        self.T = per
        # self.out = []
        self.Filter(x)

    def Filter(self, x):
        a0 = 1/(1+self.T/(2*math.pi))
        b1 = self.T/(2*math.pi)/(1+self.T/(2*math.pi))
        self.out = []
        for i in range(0, len(x)):
            if i == 0:
                self.out.append(x[i])
            else:
                self.out.append(a0*x[i]+b1*self.out[i-1])

    # 1-я производная
    def d1out(self, i):
        if i == 0:
            return 0
        return self.out[i]-self.out[i-1]

    # 2-я производная
    def d2out(self, i):
        if i == 0:
            return 0
        elif i == 1:
            return self.out[i]-self.out[i-1]
        return self.out[i]-2*self.out[i-1]+self.out[i-2]


# Фильтр среднее за период (подходит для калибровки) T - целое
class cFMean():

    def __init__(self, per, x):
        self.T = per
        # self.out = []
        self.Filter(x)

    def Filter(self, x):
        self.out = []
        for i in range(0, len(x)):
            if i == 0:
                self.out.append(x[i])
            elif i > 0 and i < self.T:
                self.out.append(self.out[i-1]+x[i]/self.T-x[0]/self.T)
            else:
                self.out.append(self.out[i-1]+x[i]/self.T-x[i-self.T]/self.T)

Кроме F1Bat(), там еще дополнительно введено простое скользящее среднее cFMean() — иногда бывает нужно.
Теперь скопируем текст в в файл Filters.py. В папке SmartLab (см. пред-й топик [1]) создадим папку SLPack, и поместим в нее наш файл Filters.py. Индикаторы готовы к использованию.

Теперь остается проверить работоспособность кода и калибровки индикаторов. Для этого напишем небольшой код и сохраним его в файле Calibr.py в папку SmartLab.

# -*- coding: utf-8 -*-
"""
Created on Mon May 12 10:09:55 2020

@author: 3Qu
"""

import matplotlib.pyplot as plt
import SLPack.Filters as flt  # загрузка нашего пакета с фильтрами

# создаем тестовую последовательность 1(t) - единичный скачок
x = [1 for i in range(0, 50)]
x[0] = 0

# создаем и инициализируем индикаторы
FM40 = flt.cFMean(40, x)
F40 = flt.cF1Bat(40, x)

# отображаем индикаторы на графике
plt.plot(FM40.out, label = 'FM40')  # добавили ярлык на график
plt.plot(F40.out, label = 'F40')
plt.title('Реакция на 1(t)')  # заголовок
plt.legend()  # отображаем ярлыки и легенду (если есть)
plt.grid()
plt.show()

Запускаем файл Calibr.py на исполнение и получаем картинку:

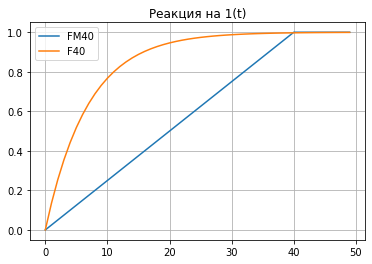
Как видим, все работает и идеально откалибровано, что и следовало ожидать от правильно построенного фильтра.
Думаю, теперь вы можете самостоятельно построить наши индикаторы на графике случайного блуждания [1], вывести на график заголовок, ярлыки и поэкспериментировать со всем этим.
Удачи!

Ссылки.
1. Моделирование Торговых Систем на Python. 1.