Как заработать на случайном блуждании. Часть 6.
В продолжение темы https://smart-lab.ru/blog/612608.php, хотелось бы добавить небольшое исследование.
Итак, мы остановились на том, что приращения рыночных котировок представляют собой расстояния, которое проходит броуновская частица за экспоненциальное время.
Еще раз смотрим на интегрированный процесс по таким приращениям:
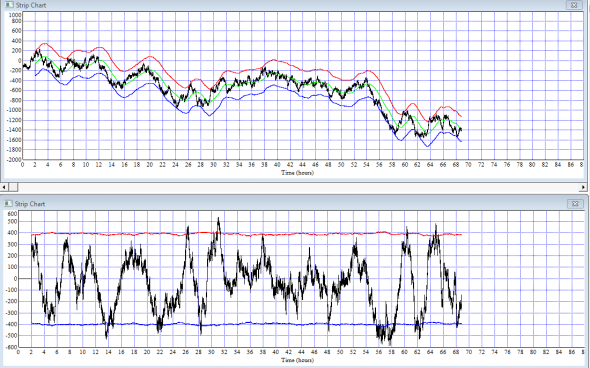
Хорошая модель, но… Не хватает главного — ответа на вопрос: а откуда берется нестационарность дисперсии реального рыночного процесса?
Ведь дисперсионный канал ±(sqrt(2*D*t)) на нижнем графике суммы приращений в скользящем временном окне практически =const, а на деле:
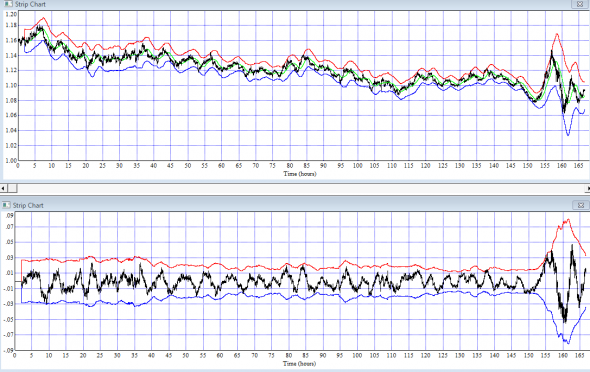
дисперсионный канал далеко не является постоянной величиной и подвергается необъяснимым отклонениям от const.
Необъяснимым ли? Хммм… Попробуем разобраться.
Итак, мы приняли за рабочую гипотезу, что распределение вероятности рыночных приращений — это произведение СВ гауссовского и экспоненциального (или в общем случае — Эрланга) распределений.
Распределение Эрланга отвечает за интервалы времени между тиковыми котировками и генератор таких чисел выглядит так:
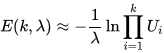
Здесь Lambda — интенсивность потока событий (котировок).
Если Lambda=const, то данный процесс — стационарный, но на рынке интенсивность потока разная в разные моменты времени, т.е. Lambda=f(t), что определяет нестационарность процесса в целом.
Попробуем смоделировать нестационарную интенсивность потока рыночных котировок. Пусть Lambda определяется равномерным случайным распределением в интервале [0;1].
Получаем:
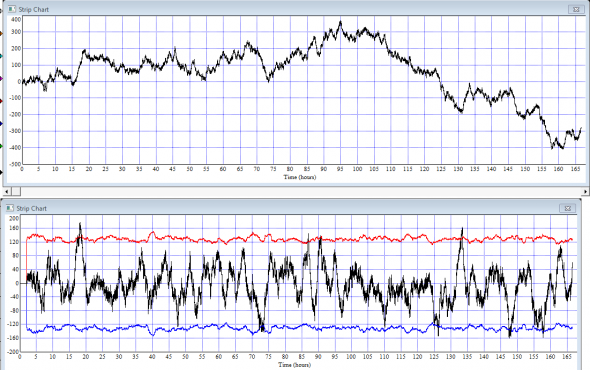
Да, дисперсия приобрела очевидную нестационарность и наша модель все более начинает напоминать реальный рыночный процесс.
Становится очевидным, что основным фактором, определяющим поведение рыночного процесса, является плотность тикового потока котировок во времени.
Учет этой величины — тиковых объемов (количества полученных тиков в единицу времени) — является определяющим для любой ТС, претендующей на Грааль. Либо — необходим переход к эквиобъемным (равнотиковым) барам.
Грааль… One love, one destiny… Ты будешь найден.
Toddler.
если плюсовые минусовые таким образом суммировать ища выход за некий «экстремум» по принципу подсчета карт в блек джеке тоже ничего не выйдет на таком простом условии.
но в целом поиск дело благородное считаю.
сие имеет специфичное название — ликвидность инструмента.
и ясный пеппер, что торговая система должна учитывать ликвидность инструмента, на котором она работает.
И движение нельзя считать броуновским, если каждые несколько минут происходит фазовый переход...
Один участник ушел и счета полетели. Ну это так, информация к размышлению ))
Надо хотя бы ступенчатым делать. То есть своя константа на каждый день. Это ближе к реальности.
Ни на чём не основанное утверждение.
Полно случаев когда шпилькой / импульсом достигают уровня, целевого или промежуточного. Тики при этом накопиться не успевают, то есть вычислить по накоплению это нельзя. А предсказывать уровень из других соображений можно.
А пытался ли кто-нибудь из искателей «грааля» дать ему формальное определение? Или же «любовь» и «судьба» не поддаются формализации?
Но тогда это из разряда «пойди туда, не знаю куда, принеси то, не знаю что».
А вот если формализовать, то поиски его приобретут характер технической задачи. С пониманием «что», «куда», «зачем».